ARC 做题笔记 - ARC160~ARC164
ARC160
A. Reverse and Count
我日，差点被打爆了/xk。
暴力排序是 \(O(n^3)\) 的，我们考虑优化这一过程。
注意到我们每次按位比较。注意到会影响到这一位的翻转区间只有 \(O(n)\) 个，我们把这些区间拉出来，记为 \(seg_1,seg_2,\ldots,seg_k\)，设剩下的区间集合为 \(S\)，那么我们一定能确定 \(seg_{i_1},seg_{i_2}\leq\ldots\leq S\leq \ldots\leq seg_{i_k}\)。递归处理 \(S\)。这样就完成在 \(O(n)\) 的时间复杂度内对 \(n\) 个操作序列确定位置，所以总复杂度 \(O(n^2)\)。
Submission #48707910 - AtCoder Regular Contest 160
B. Triple Pair
板子题。钦定 \(x>y>z\)。直接考虑对 \(x\) 根号分治。\(x\leq \lfloor\sqrt{n}\rfloor\) 的时候答案直接是 \(\lfloor\sqrt n\rfloor^3\)。否则要求 \(y,z\leq \lfloor\dfrac{n}{x}\rfloor\)。对 \(x\) 做整除分块即可。根号分治的目的是保证讨论的一直是最大值。
Submission #48708124 - AtCoder Regular Contest 160
C. Power Up
也是简单题。考虑 \(f(i,j)\) 表示到数字 \(i\) 剩下 \(j\) 个的方案数，单次转移是 \(O(1)\) 的。乍一看状态数不对，但考虑每一个数字 \(i\)，其数字个数对第二维大小的贡献应该是 \(\sum\limits_{j=0} \dfrac{cnt_i}{2^j}\leq 2cnt_i\)，即考虑其对 \(f(i),f(i+1)\) 的贡献之和。而 \(\sum\limits_{i=1}^n cnt_i=n\)。所以第二维的大小总和即总状态数是 \(O(n)\) 的，然后就做完了。
Submission #48708772 - AtCoder Regular Contest 160
D. Mahjong
从这里开始上了强度。
奇怪数数题先找点充要条件，一个什么样的序列是合法的？
首先注意到两个操作都不会改变模 \(k\) 意义下的余数，所以显然上来要求 \(m\equiv 0\pmod k\)。
然后注意到对同一个位置操作 \(k\) 次 \(2\) 操作等价于对这 \(k\) 个位置分别做 \(1\) 操作，那么我们可以强行钦定每个位置上的 \(2\) 操作数量不超过 \(k-1\)。
注意到对一个位置做 \(1\) 操作不会改变其在模 \(k\) 意义下的余数。因此位置 \(i\) 必须恰好被 \(a_i\bmod k\) 次 \(2\) 操作覆盖。这意味着对于一个合法的序列，如果我们钦定每个位置的 \(2\) 操作数量不超过 \(k-1\)，则操作方案应当可以唯一确定。即在第一个位置上做 \(a_1\bmod k\) 次 \(2\) 操作，第二个位置做 \(a_1\bmod k+(a_2-a_1)\bmod k\) 次，以此类推。
但是有一个问题，我们如果做 \(2\) 操作把 \(a_i\) 变成了负数将会非常麻烦。怎么办？考虑把整个过程倒过来，把操作变成单点加和区间加。注意到我们钦定了 \(1\) 操作和 \(2\) 操作数量且 \(2\) 操作数量小于 \(k\) ，操作序列和最终合法的序列仍然满足双射关系。
现在问题变成了对操作计数。令 \(f(i,j)\) 表示考虑到位置 \(i\)，前面的操作次数为 \(j\) 的方案数。转移分别枚举做哪种操作，具体转移式写在下面。
这样我们就有了一个 \(O(nm^2)\) 做法，但是复杂度疑似有点高。
然后我死在这了/cf。
然后开始魔法。记 \(F(i)\) 为 \(f(i,*)\) 的 OGF。拿生成函数刻画转移。
酷！这样答案就是 \([x^{\frac{m}{K}}] (\dfrac{1}{1-x})^{2n-K+1}(1-x^K)^{n-K+1}\)。
对前后进行一个二项式定理，然后暴力卷积状物暴力算组合数出系数。注意到你只需要算一项所以卷积的枚举量是 \(O(n)\) 的，然后带上组合数是 \(O(n^2)\)。
式子放在下面。
酷！
Submission #48709472 - AtCoder Regular Contest 160
E. Make Biconnected
强度下去了/hanx。这个题评铜牌是不是有点高了。
首先进行一些观察，定义 \(leaf\) 是所有度数为 \(1\) 的点构成的集合，那么答案的下界一定是 \(\sum\limits_{u\in leaf} W_u\)。原因是每个叶子至少连出去一条边，否则删去叶子唯一连边的另一端点即可让叶子和剩余部分不连通。
下面我们考虑能否达到这个下界。
若 \(|leaf|\equiv 0\pmod 2\)，我们可以说明这个下界总是可以取到。设 \(dfn(u)\) 表示 \(u\) 号点的 dfs 序，我们将叶子按照 \(dfn(u)\) 排序，记排序后第 \(i\) 个点为 \(leaf_i\)，同时记 \(mid=\dfrac{|leaf|}{2}\)。我们进行如下操作，将 \(leaf_i\) 向 \(leaf_{i+mid}\) 连边。其中 \(i\in[1,mid]\)。证明考虑把树拍到欧拉序上，然后考虑每个叶子所在的分组，结合 \(d\leq 3\) 容易证明（另：我记得这个性质对于所有树成立，不知道对不对）。
然后考虑 \(|leaf|\equiv 1\pmod 2\)。考虑把剩下的叶子和某个点连边，不难想到我们希望一定是和 \(W_x\) 最小的那个 \(x\) 连接。唯一的问题是 \(x\) 存在于 \(u\) 到其上方第一个度数不小于 \(1\) 的点的路径的中间，这种时候我们只需要换一个叶子即可。唯一的 corner case 是一个点挂三条链，这个时候我们再判一下次小值即可。
Submission #48711805 - AtCoder Regular Contest 160
F. Count Sorted Arrays
恐怖题。
我们定义一次交换操作是有用的，当且仅当其至少让所有排列当中的一种排列发生改变。
考虑有效交换的次数。假设一次交换操作是 \((u,v)\) 是有效的，首先它会使 \((u,v)\) 变成无效。同时它可能会使一些 \((k,u),(v,k)\) 从无效变为有效，我们很难直接断言有效交换的数量的变化情况，但显然其不会影响 \((i,j),i,j\not\in \{u,v\}\) 的有效情况，因此考虑进行一些分类讨论。
-
\((k,u)\) 变为有效。
此时 \(a_u>a_k>a_v\)。注意到原来 \((k,v)\) 现在由有效变为无效，抵消掉了 \((k,u)\) 带来的贡献，所以总有效操作数量减一。
-
\((v,k)\) 变为有效。
此时 \(a_u>a_k>a_v\)。注意到原来 \((u,k)\) 现在由有效变为无效，抵消掉了 \((v,k)\) 带来的贡献，所以总有效操作数量减一。
因此我们说明了有效操作的数量单调递减。这意味着有效操作只有 \(O(n^2)\) 个。如果我们能快速判断一个操作是否有效，同时可以快速维护有效操作带来的变化，这个题就做完了。
我们考虑对排列进行一些世界级映射。注意到每个排列恰好对应了 \(n\) 维平面上从 \((0,0,\ldots,0)\) 走到 \((1,1,\ldots,1)\) 的一条路径，每次可以让任意一维坐标加 \(1\)，在第 \(i\) 步在 \(p\) 位置加 \(1\) 意味着 \(a_p=i\)。此时路径上的第 \(i\) 点的第 \(p\) 个二进制位为 \(1\) 意味着在排列中第 \(p\) 个位置上的数字不大于 \(i\)。
我们重写一下排列的判定条件。一个排列可以在若干次操作后排好序，当且仅当把路径上的每一个点看做 \(01\) 序列后顺次执行交换操作其变为有序。我们成这样的点为好点、这意味着合法排列的数量相当于从 \((0,0,\ldots,0)\) 仅经过好点走到 \((1,1,\ldots,1)\) 的路径数量。容易 \(O(2^n n)\) 解决。
同时，我们可以暴力模拟每个点看做序列顺次执行交换操作后当前的序列是什么样子的，因此我们可以简单以的 \(O(2^n n)\) 的复杂度在每次操作结束后判定一个点是否是好的。
最后我们需要判定操作是否有效。结合上面的结论，我们在每次执行有效操作后暴力重构所有 \((k,u),(v,k)\) 操作的合法性。这个复杂度也是 \(O(2^n n)\) 的。
总有效操作次数为 \(O(n^2)\)，所以总复杂度为 \(O(2^nn^3+m)\)。
Submission #48715812 - AtCoder Regular Contest 160
ARC161
A. Make M
比较简单的题。首先考虑是非严格大于的做法，那么我们把序列排序后劈成两半然后做类归并状物即可。
然后现在我们要相邻的不相等，那么我们把大的部分和小的部分全部从大到小排以后拼到一起即可，感性理解的话，让较大的和较大的匹配一定能使得相邻两个数的差尽可能大。
Submission #48347711 - AtCoder Regular Contest 161
B. Exactly Three Bits
注意到答案一定从低到高是抹掉 \(n\) 的若干数位，直到 \(\mathrm{popcount}(n)\) 恰好 \(3\)。现在唯一的问题是 \(n\) 的数位不足 \(3\)，那么我们只需要每次把 \(n\) 减一直到 \(\mathrm{popcount}(n)\) 不小于 \(3\) 为止。容易证明这个操作次数不会超过 \(4\) 次。
Submission #48356115 - AtCoder Regular Contest 161
C. Dyed by Majority (Odd Tree)
考虑给每个点钦定颜色，分为颜色不定，为白色和黑色考虑。从下到上 dfs 整棵树，把当前该节点的所有儿子中颜色不定的设为当前的颜色，设度数为 \(deg\)，然后如果儿子中和其颜色相同的数量小于 \(\lfloor\dfrac{deg}{2}\rfloor\) 则一定无解，若为 \(\lfloor\dfrac{deg}{2}\rfloor\) 则去钦定其父亲的颜色，否则该点父亲颜色不定，一直做到根。最后把依据此方案构造出的颜色设为答案，特别的，若根节点颜色不定，则在上面随便填一个颜色。
Submission #48426001 - AtCoder Regular Contest 161
D. Everywhere is Sparser than Whole (Construction)
若至题/bobo。
如果 \(nd>\dfrac{n\times (n-1)}{2}\) 则无解，否则直接构造 \(E=\{i\in[1,n],j\in[1,d]\vert (i,(i+d-1)\bmod n+1)\}\)。图的简单性可以证明，然后考虑证明稀疏性。对于任意一个子图 \(G\)，令 \(G_k\) 表示 \(G\) 中仅由 \((i,(i+d-1)\bmod n+1)\) 的边和点构成的子图。容易发现对于任意 \(G_k\) 每个点的度数不超过 \(2\)，即 \(G_k\) 密度不大于 \(1\)。所以总的密度不超过 \(d\)。
E. Not Dyed by Majority (Cubic Graph)
牛逼题/pz。
注意到合法的解不会很多（我去哥们你咋注意到的），所以我们可以随机一个解，然后判定这个解是否合法。考虑判定一个颜色序列是否可以被构造。对于每一个点，如果其颜色为黑，则其周围点至少有两个黑点。令周围三个点为 \(u,v,w\)，\(col(u)\) 代表 \(u\) 号点的颜色，其中 \(0\) 为白色，则要求 \((col(u)\lor col(v))\land (col(v)\lor col(w)) \land (col(u)\lor col(w))\)。这个限制可以直接 2-SAT 描述，最后判定 2-SAT 是否有解即可。
关于合法的解占比的数量级，官方给出的估算是对于较大的 \(n\) 答案为 \(0.293\)，较小的为 \(0.48\)，感兴趣的可以阅读 Editorial 和 Supplementary 获取更多信息。
Submission #48447738 - AtCoder Regular Contest 161
F. Everywhere is Sparser than Whole (Judge)
完全没看证明，所以写的东西比较意识流。
先判掉图不连通的情况。首先有最大密度子图转最小割的做法。记最小割为 \(f\)。然后我们可以根据 \(nm-f\) 的正负性判断答案存在大于 \(D\) 的子图。然后考虑判等于 \(D\) 的情况。注意到那个最小割做法是把度数和边拆开算，这个限制条件相当于有边满流。所以我们现在直接把原图中的边的容量设成 \(1-eps\)，此时的判定为 \(nm-f'>0\)。然后这个东西可以和前面的合起来做。
Submission #48194665 - AtCoder Regular Contest 161
ARC162
A. Ekiden Race
比较唐的一个题。考虑一个人 \(i\) 在第二段中一定比另一个人 \(j\) 快的条件，不难发现为第一段 \(i\) 慢于 \(j\)，综合 \(i\) 快于 \(j\)。这意味着可能成为第一的只有 \(p\) 为后缀最小值的那些，从后向前扫即可。
Submission #48918643 - AtCoder Regular Contest 162
B. Insertion Sort 2
注意到题面干的事情实际上是捆绑两个数做插入排序。因此我们考虑直接做插入排序，第 \(i\) 轮中将 \(i\) 和其后面的数绑定，然后插到对应位置。有一个问题是 \(i\) 在最后一个。不难想到把 \(i\) 和前一个打包先前移再后移。再考虑无解，naive 的想法是如果做到最后两个数不按顺序就无解。这是对的，但是我使用了另一种方式，把插入看成若干次交换，对每次交换涉及到的三个数的大小关系进行讨论，发现逆序对数奇偶性不变。因此无解当且仅当逆序对为奇数。
Submission #48929123 - AtCoder Regular Contest 162
C. Mex Game on Tree
注意到 Bob 只会填 \(k\)，一个子树内如果有 \(k\) 则结局 \(\text{mex}\) 一定不是 \(k\)。所以先手必胜当且仅当存在一个子树进行不超过一次操作后 \(\text{mex}\) 直接变为 \(k\)，因此做完了，对每个节点维护长度为 \(k\) 的 bitset，然后暴力或上每个儿子的 bitset 得到子树内的数字存在性，检查其中 \(0\) 的个数即可。时间复杂度 \(O(\dfrac{nk}{\omega})\)。
Submission #48934844 - AtCoder Regular Contest 162
D. Smallest Vertices
很魔怔的一个题。
先想想本质不同合法无根树数量。这个是 Cayley 定理和 prufer 序那一套，那就是 \(\dfrac{(n-2)!}{\prod (d_i-[i=1])!}\)。
然后我们考虑拆贡献。钦定每一个点 \(u\) 是好的，考虑方案数。假设我们现在已经钦定了一个 \(u\) 子树内的点构成的集合 \(S\)，那么首先要求 \(\sum\limits_{u\in S} d(u)=|S|-1\)。然后把 \(u\) 子树内的点和子树外的分开考虑，套上上面的那个式子，然后对 \(u\) 子树内做，再把 \(u\) 视为叶子，对子树外再套那个式子。对式子做整合可以得到下式。
注意到很棒的一点是这个式子只和 \(u\) 与 \(|S|\) 有关。不难想到设计 dp。考虑到 \(u\) 号点，当前已经选了 \(i\) 个点，度数和为 \(j\) 的方案数。容易以 \(O(1)\) 的复杂度转移。顺序转移后提取每个位置的 dp 数组，枚举选的点数以及度数和贡献到答案即可。时间复杂度 \(O(n^3)\)。
Submission #48986816 - AtCoder Regular Contest 162
E. Strange Constraints
神秘计数/yun。
考虑重写一下题意。我们要求第 \(i\) 个整数的出现次数不超过 \(a_i\)，且我们可以把出现次数不超过 \(a_i\) 的数放到位置 \(i\) 上。这启发我们按照数字的出现次数从大到小钦定。
设 \(f(i,j,k)\) 表示当前已经钦定了 \(j\) 个数，这些数的出现次数全部大于 \(i\)，且这些数一共出现了 \(k\) 次的方案数。转移时，我们枚举当前要钦定多少个数出现了 \(i\) 次，记为 \(l\)，转移到 \(f(i,j+l,k+il)\)。考虑转移时的系数，记 \(cnt_i\) 表示 \(a_j\ge i\) 的 \(j\) 数量，那么首先选出数的方案数是 \(\dbinom{cnt_i-j}{l}\)，然后选择位置，当前可用的位置一共有 \(cnt_i-k\) 个，因此位置上的方案数是 \(\dbinom{cnt_i-k}{il}\times \dbinom{il}{\underbrace{i,i,\ldots i}_l}\)。将二者相乘即为转移系数。
这个复杂度乍一看是 \(O(n^4)\) 的。但我们冷静一下，\(cnt_i\) 的量级是 \(\dfrac{n}{i+1}\) 的，\(j,l\) 枚举的上界分别不会超过 \(cnt_{i+1},cnt_i\)，因此总复杂度的上界至多为 \(\sum\limits_{i=1}^n n\dfrac{n}{i+1}\dfrac{n}{i}\)，提取出 \(n^3\)，对后面做裂项，我们容易发现复杂度上界为 \(O(n^3)\)。
Submission #48988259 - AtCoder Regular Contest 162
F. Montage
考虑题面当中的那个限制，相当于是对于任意一个子矩形，如果左上右下均为 \(1\)，则右上左下均为 \(1\)。
然后考虑合法的棋盘会长成什么样子。如果一个位置放上了 \(1\)，其左侧放上了 \(0\)，则那个 \(0\) 上方的所有格子填上的都应为 \(0\)，否则取出上方的 \(1\) 作为左上，这个 \(1\) 为右下，这就是一个不合法的矩形。同理可以推出下侧，右侧，上侧有 \(0\) 的对应限制情况。
结合上面的四个推论，我们似乎可以推出一个更强的性质。对于一行，若存在两个不在同一段的 \(1\)，则夹在那些行中间的列上的数全部应当为 \(0\)。这意味着如果我们删掉所有全为 \(0\) 的列，每一行的 \(1\) 应该全为连续段，对列也同理。而全零的行列显然不影响答案，我们可以最后乘上一个组合数把它们放回去。
接下来继续考虑连续段的分布情况。注意到在删掉空行空列后，\(1\) 构成连续段，上面的条件进一步增强，相当于要求如果左侧存在零，则左上矩形均为 \(0\)；若右侧存在 \(0\)，则右下矩形均为 \(0\)。此时 \(1\) 连续段的分布已经很明确了，删掉空行空列后在纵坐标上连续段左端点单调不减，右端点单调不减，且每行每列至少一个 \(1\)。这样就可以简单 dp 了。\(f(i,j,k)\) 表示考虑到位置 \(i\)，连续段左端点在 \(j\)，右端点在 \(k\) 的方案数。枚举当前左右端点容易做到 \(O(n^5)\)，注意到有贡献的 \(f(i,*,*)\) 是一个左下矩形，因此二维前缀和即可。复杂度 \(O(n^3)\)。
Submission #49012565 - AtCoder Regular Contest 162
ARC163
A. Divide String
显然若 \(S\) 字典序小于 \(T\)，则 \(S\) 字典序小于 \(T+T'\)。这意味着若存在合法方案则一定存在一种只划分两段，枚举分界点暴力判断即可。
Submission #49033527 - AtCoder Regular Contest 163
B. Favorite Game
注意到变化 \(A_3,A_4,\ldots,A_n\) 一定不如直接变化 \(A_1,A_2\) 优，因为后者在改变和某个数的相对距离的同时让合法区间变得更长。所以我们直接把 \(A_3,A_4,\ldots,A_n\) 排序，然后枚举到底把哪 \(m\) 个数包含进区间里即可。端点移动次数容易 \(O(1)\) 计算。
Submission #49033642 - AtCoder Regular Contest 163
C. Harmonic Mean
考虑初中数学。第一反应是裂项，但是最后补的 \(\dfrac{1}{n}\) 可能会和前面重复。因此我们进一步考虑裂项的本质。注意到其提供了等式 \(\dfrac{1}{x}=\dfrac{1}{x+1}+\dfrac{1}{x(x+1)}\)。这意味着我们可以考虑先把 \(1\) 裂成 \(\dfrac{1}{2},\dfrac{1}{3}\) 和 \(\dfrac{1}{6}\)。然后每次持续分裂最小的分数，直到不同的分数个数超过 \(n\) 个即可。
Submission #49033782 - AtCoder Regular Contest 163
D. Sum of SCC
不会大套路题/ng。
竞赛图中强连通分量数等于把点集划分为两个集合 \(A,B\)，且满足对于所有边 \((u,v),u\in A,v\in B\)，边的方向为 \(u\rightarrow v\) 的方案数减一。
考虑证明。对于一个竞赛图，其缩点后一定为一个竞赛图 DAG，这个 DAG 有很强的性质是拓扑序固定，所以所有合法的分发一定是取拓扑序的一段前缀放到 \(A\)，一段后缀放到 \(B\) 这个样子，因此上命题得证。
因此我们直接开始对划分方案计数。\(f(i,j,k)\) 表示考虑到位置 \(i+j\)，分别划分出 \(i,j\) 个到 \(A,B\) 集合中，有 \(k\) 条边满足 \(u<v\) 的方案数。转移时枚举当前点划分到那个集合，钦定所有向当前集合内连边的方向即可。
复杂度 \(O(n^3m)\)。
Submission #49034510 - AtCoder Regular Contest 163
E. Chmin XOR Game
更魔怔了这个题。
从二维情况入手，我们打个表先。
0111 1111 1111 1111
1100 1111 1111 1111
1010 1111 1111 1111
1001 1111 1111 1111
1111 1111 0111 0111
1111 1111 1100 1100
1111 1111 1010 1010
1111 1111 1001 1001
1111 0111 1111 0111
1111 1100 1111 1100
1111 1010 1111 1010
1111 1001 1111 1001
1111 0111 0111 1111
1111 1100 1100 1111
1111 1010 1010 1111
1111 1001 1001 1111
我们很难注意到这个图大图和子图同构。
然后我们考虑这个图当中先手必胜的位置。先观察一个子图。注意到先手必胜当且仅当 \(((a\neq 0\lor b\neq 0)\land(a=0\lor b=0))\lor a=b\)。而同构的条件意味着只要有二进制相邻两位满足这个条件就可以。
我们先考虑这样一件事，如果只考虑值域在 \([0,3]\)，什么样的 \(2\times 2\) 是先手必胜的。我们猜想，必胜状态集合和先手一次操作就能结束等价，证明是容易的，考虑每次操作至少抹掉一个二进制位，而一旦不能一步转移则至少需要操作三次，这对值域为 \(4\) 的情况一定不可能。
然后我们尝试证明同构这件事。注意到其前若干位相当于一次可以做也可以不做的转移。因此如果前若干位可以转移一次或多次，则先手一定可以通过在前若干位做先后手交换，因此先手必胜，剩下就是先手只能操作一次的，这样相当于直接做后两位。
注意到上述过程和 \(n=2\) 没有依赖关系，所以可以直接推广到 \(n>2\)。
Submission #49035479 - AtCoder Regular Contest 163
F. Many Increasing Problems
先考虑 Increasing Problem 怎么做，这是经典的 slope trick，我们每次在集合中加入两个 \(a_i\)，然后删去最后一个拐点，将堆顶和拐点的差统计入答案。
考虑经典套路，枚举一个值 \(v\)，将所有不超过 \(v\) 的看做 \(0\)，超过的看做 \(1\)，然后对这个问题做 slope trick，对 \(v\) 答案求和得到的答案显然和原问题相等。
然后考虑这个问题是什么，我们有一条折线，从 \((0,0)\) 走到 \((n,*)\)。每次碰到 \(0\) 向下，反之向上，碰到 \(y=0\) 则不向下走，零一序列的答案即为向下走的次数。但这个不好直接做。我们考虑每出现一次向下走就抬高起点，这样第二个不向下走的条件就直接没了。所以我们现在相当于把起点扛到 \((0,x)\)，走到 \((n,y)\) 的向下走的次数。同时我们钦定必须碰到 \(y=0\)。这是经典的反射容斥，我们可以直接推式子。这样枚举 \(x\) 和 \(y\) 和 \(v\) 就有一个 \(O(n^3)\) 的做法。
懒了，不详细写式子推导了，列几个我觉得比较重要的点。
相当于是要化简求和下式。
首先化简那个 \(x^i(m-x)^{n-i}\)，对这个做等比数列求和以后分治通分就可以直接得到对于固定 \(i\) 的 \(x^i(m-x)^{n-i}\) 的值。然后当成系数。继续换元 \(k=i-j\) 观察求和形式，上面的 \(j\) 变成 \(k-i\)。对于 \(k\) 的部分是直接前缀和，另一部分大部分抵消可以 \(O(1)\) 计算。因此枚举 \(k\) 就直接做完了。
瓶颈在那个等比数列求和后分治通分做求逆。复杂度 \(O(n\log^2 n)\)。
Submission #49046196 - AtCoder Regular Contest 163
ARC164
A. Ternary Decomposition
考虑一个答案的下界和上界，显然分别是 \(n\) 的 \(3\) 进制分解的数位和 \(dsum\) 与 \(n\)。我们考虑是如何从上界走到下界的，每次我们找到一个第 \(i\) 位的 \(1\)，将其下推为 \(3\) 个 \(i-1\) 位的 \(1\)。在这个过程中，我们需要的 \(3^x\) 个数恰好增加了 \(2\)。这意味着其恰好取遍 \([dsum,n]\) 中每一个和 \(dsum\) 奇偶性相同的数。因此只需要判断范围和奇偶性即可。
Submission #49211251 - AtCoder Regular Contest 164
B. Switching Travel
考虑一个合法的回路是什么样的，注意到在不产生环的前提下，我们每条边如果能走一定只能走一次。先经过若干条边 \((u,v)\)，满足 \(c_u\neq c_v\)，我们称经过的点集为 \(V\)，此时 \(V\) 中的点集全部反色。然后走一条边 \((u,w)\) 满足 \(w\in V\)，此时在原来的颜色中应当有 \(c_u=c_w\)。所以我们有了一个做法，用并查集维护所有异色边构成的连通块，然后查询每条同色边的两端点是否在同一连通块中。如果存在，则我们可以依据上述方案构造一条路径。
Submission #49211650 - AtCoder Regular Contest 164
C. Reversible Card Game
我们考虑把所有正面大于背面的数字视为 \(0\)，背面大于正面的数字视为 \(1\)。考虑在全 \(1\) 的情况下，Bob 的策略一定是 Alice 每次把一个 \(1\) 变成 \(0\)，然后 Bob 取走这个 \(0\)。而在非全 \(1\) 的情况下，Bob 至多只会面对一次在 Alice 翻过的情况下全 \(1\) 的局面。因此我们只需要讨论 Bob 是否会取 \(1\)，以及取哪个卡牌为 \(1\) 即可。
考虑第一个问题。我们注意到每一轮操作在存在 \(0\) 的情况下 Bob 一定选择 \(0\)，而 Alice 的操作又会使 \(0\) 的奇偶性恰好改变 \(1\)。因此无论 Alice 如何操作 \(0\) 的奇偶性一定不变。所以 Bob 会面临全 \(1\) 局面当且仅当有奇数个 \(0\)。而如果取 \(1\) 我们一定取极差最小的那个。容易证明，Bob 可以通过不管这个 \(1\) 来优先去掉其余的 \(0\)，然后做到取到这个极差的目的。所以判断奇偶性以后减去极差最小值即可。
Submission #49211895 - AtCoder Regular Contest 164
D. 1D Coulomb
首先考虑固定序列怎么求答案。由于小球相撞抵消电性不影响任意一侧小球对应方向的代数和，所以每个小球运动方向永远不变。答案相当于每个小球移动的路径长度和，我们不妨将每一对匹配的小球 \((u,v)\) 由两侧向中间移动变为 \(u\) 向 \(v\) 移动且 \(v\) 不动。容易发现这样答案不变。这样我们就有了简单做法，考虑维护一个栈，每遇到一个反电性的小球就消去栈顶，统计两者距离贡献到答案，否则加入栈中，做到序列末尾停止。
考虑怎么应用到 dp 上。我们对上述做法略作改动，贡献提前计算，每次移动时将答案加上栈的大小。现在就有简单 dp 做法了。令 \(f(i,j,0/1)\) 表示考虑到位置 \(i\)，栈中有 \(j\) 个正/负电性的小球的答案。同时为了转移，再记 \(g(i,j,0/1)\) 表示方案数。转移枚举当前小球电性，类似序列做法转移即可。
需要滚动数组，时间复杂度 \(O(n^2)\)。
Submission #49212447 - AtCoder Regular Contest 164
E. Segment-Tree Optimization
考虑把整个序列看成一条链，在每一层中，我们可以选择当前区间的链，断开中间的一条边，然后将两条链下放到下一层中。而此时第一问的答案相当于是求出 \(l-1\rightarrow l\) 和 \(r\rightarrow r+1\) 两条边断开的层数的较大值。我们标记所有要被断掉的边，则第一问的答案就是对这些边正常建线段树的高度。
然后考虑第二问。对上述断点建线段树后底层是若干区间，我们考虑一个区间会造成怎样的贡献。对于划分出的一个区间，我们要么直接放到上层，要么放到底层，然后和一个区间合并再挂到上层。有贡献的只有第二类。考虑这种合并会造成什么样的贡献。假设我们需要合并区间 \([l,mid),[mid,r]\) 并放到最底层，那么只有那些被 \([l,r]\) 包含或和 \([l,r]\) 相交的区间会遍历到最底层。而由于这些区间位于最底层，所以对于造成贡献的查询区间，它们要么左端点为 \(mid\)，要么右端点为 \(mid-1\)。同时，唯一的限制条件是上层节点个数不大于 \(2^{d-1}\)。因此我们可以做 dp 了。\(f(i,j)\) 表示考虑到第 \(i\) 个区间，上一层有 \(j\) 个区间的答案。转移枚举上面的两种操作分别向对应位置取最小值即可。
时间复杂度 \(O(n^2+q)\)。
Submission #49213648 - AtCoder Regular Contest 164
首先注意到，每个节点上棋子被翻转次数是固定的。如果我们钦定根节点的深度为 \(0\)，则每个节点上的棋子被颜色翻转的次数为其深度。
而棋子最终的颜色只和被反转次数的奇偶性和初始时的颜色相关，所以这个问题可以被转化为如下一个等价问题。
给定一个 \(n\) 个点的树，每个点有红蓝两种颜色，根节点颜色为红色，每个节点的颜色和其父亲的颜色相反。两个人轮流在树上放黑白两种棋子，执白先手。每次挑选一个叶子，放上一枚棋子，并删去这个叶子。在蓝色节点上的棋子最终会变为对方棋子的颜色，在红色节点上的将会变为自己的颜色。双方的目标都是最大化自己颜色的棋子的数量，询问最终局面白色棋子的数量。
转化成这个问题最大的好处是让每个节点之间相对独立，现在节点间唯一的限制是放棋子的点只能是叶子。
同时，我们对白色棋子的数量换一种描述。设 \(a\) 表示 Alice 下在蓝色节点上的棋子数量，\(b\) 表示 Bob 下在蓝色节点上的棋子数量，则答案可以表示为 \(\lceil\dfrac{n}{2}\rceil-a+b\)，这个的好处是更直观的理解下面贪心策略的正确性。
考虑进一步简化局面。如果当前存在红色叶子，双方的策略显然都是先把棋子下在红色叶子上。因此我们可以看做是先把所有红色叶子丢掉，那么现在的局面变成了只有蓝色叶子的情况。我们称这种局面为简化局面一。
进行到简化局面一会有一些先后手的变换，为了避免混淆，我们下文中的先后手均指当前局面的先后手，用 Alice 和 Bob 代替原局面的先后手。
当只有蓝色叶子的时候，双方只能取蓝叶子。但如果先手结束操作以后，出现了一个红叶子，那么后手一定会直接取掉新生成的红叶子。这样先后手不变，后手净赚两个节点。
根据贪心策略，无论先手后手都一定会尽量避免这种情况的发生，也就是说，先手后手将尽量取那些不会产生新红叶子的蓝叶子，直到不存在这样的蓝叶子。我们称这种局面为简化局面二。
现在局面进一步简化。我们现在取任意一个蓝叶子都会使得一个新的红叶子生成。然后我们套用简化局面一去掉那个新产生的红叶子。此时局面走向了两种情况。一种是直接成为了简化局面二，另一种则是产生了不会产生新红叶子的蓝叶子。根据简化局面二的定义，只会产生一个这种蓝叶子。
我们进一步讨论简化局面二做一次操作后得到的局面。此时的先手一定希望尽量快的将自己变为后手（否则每一步均会亏两个节点），考虑什么时候先手才能达到这个目的，我们发现，先手能够达到这个目的当且仅当产生了不会产生新红叶子的蓝叶子。此时，先手取掉这个蓝叶子，局面成为简化局面二，且先后手互换。
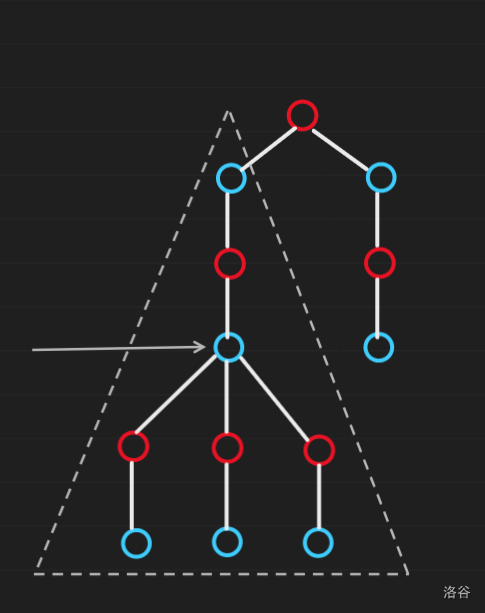
我们称一个树上连通块是簇，当且仅当其由一个父亲度数大于 \(1\) 的蓝色节点为根和若干蓝红交替的链组成；称一个簇的代价为其中的节点个数。那么我们发现，先手的策略是每次取掉这样一个簇，如果先手是 Alice，则使得答案减少簇的代价，否则增加簇的代价；删掉这个簇，然后先后手互换。
下面给出了一个簇的例子。
图中虚线部分构成了一个簇。注意灰色箭头指向的节点的子树不构成簇，原因是父亲度数不大于一。
根据贪心的策略，我们有猜想是，先手每次会取代价最小的簇，这个策略的正确性是非常容易证明的，因为先手每多做一次操作均会导致两个节点的亏损。严谨证明可以参考 Atcoder 的官方题解，这里不再赘述。
根据这个猜想，我们得到了这个题的多项式做法，首先把局面变为简化局面一，然后按照每次取出最小的簇，删掉，贡献答案，交换先后手，重复操作直到树被删空。特殊的，当树中不存在簇时，我们认为剩下的节点为一个大簇。时间复杂度 \(O(n^2)\)。
考虑降低这个做法的复杂度。我们从下向上划分簇。对于每个蓝色节点，其可能成为一个簇的根节点，我们将其放到父亲红色节点考虑。而对于红色节点，按照上述策略，其将保留最大的那个簇向上传递到其父亲，同时确定其余簇的形态。我们容易使用排序完成这一过程。时间复杂度 \(O(n\log n)\)。
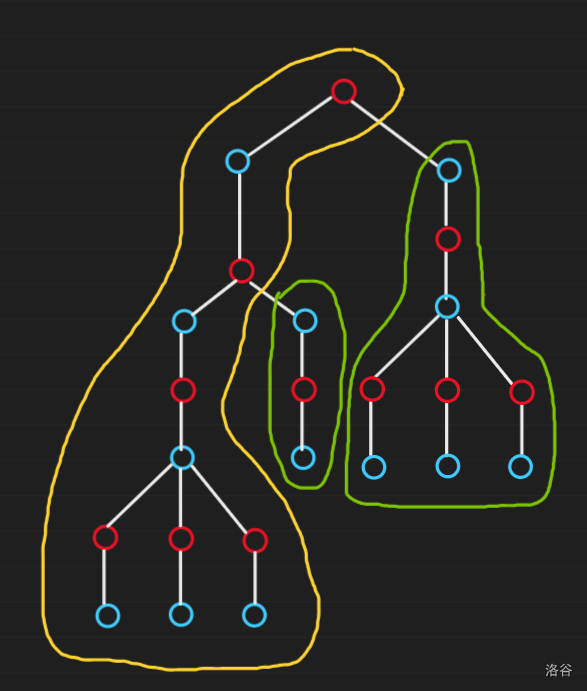
下面描述了一个簇的划分过程。
图中的所有绿色部分为确定的簇，黄色部分将随红点继续上传参与以其祖先节点为根的簇的构成
同时，为了减少代码细节，我们将单独的红色叶子看为一个代价为 \(0\) 的簇。这样我们依次确定每一个簇后，按照代价排序，先后手依次取簇贡献答案即可。
综上，我们在 \(O(n\log n)\) 的复杂度内解决了这个问题。
