迪杰斯特拉算法

迪杰斯特拉（Dijkstra）算法是最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心一层一层的向外走（广度优先搜索），直到找到终点

先看具体的例子来体会下它的算法思想：

 

 

 

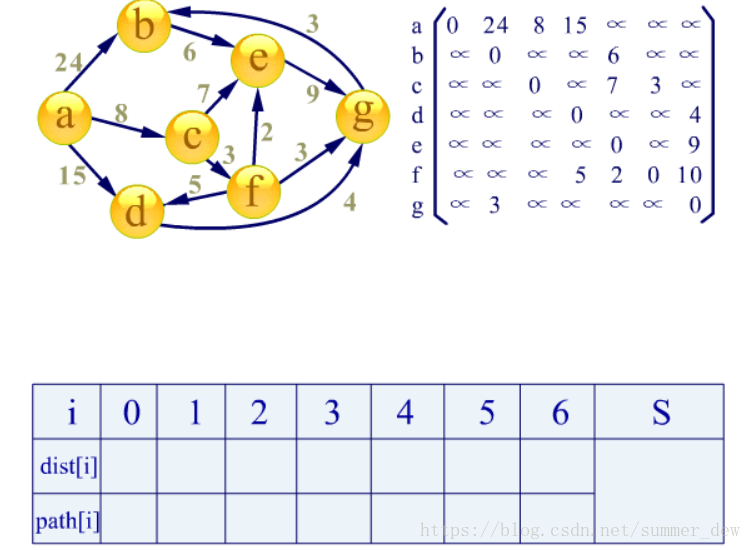
• dist[]：起点到未被并入的顶点的最短距离
  【类比】Prim算法中的lowCost[]：当前生成树到为并入的顶点的最短距离
• path[]：起点到该顶点的最短路径
• S[]：已并入的顶点

 

步骤

【第一步】

 

【第二步】

 

 

【步骤三】

 

 

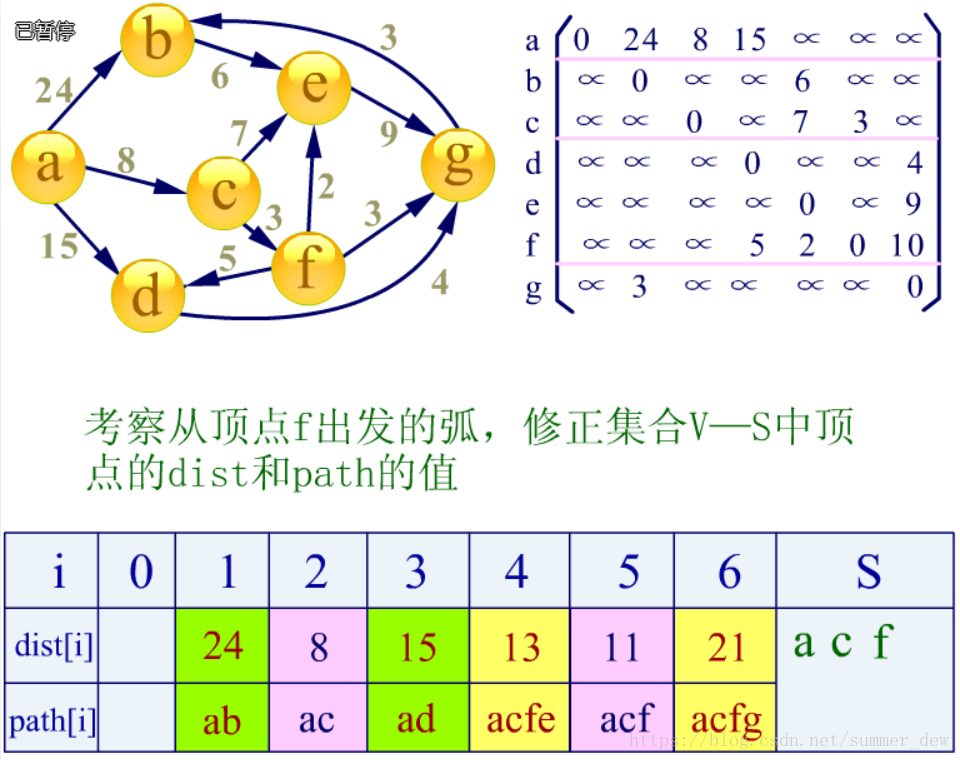
【步骤四】

 

 

 

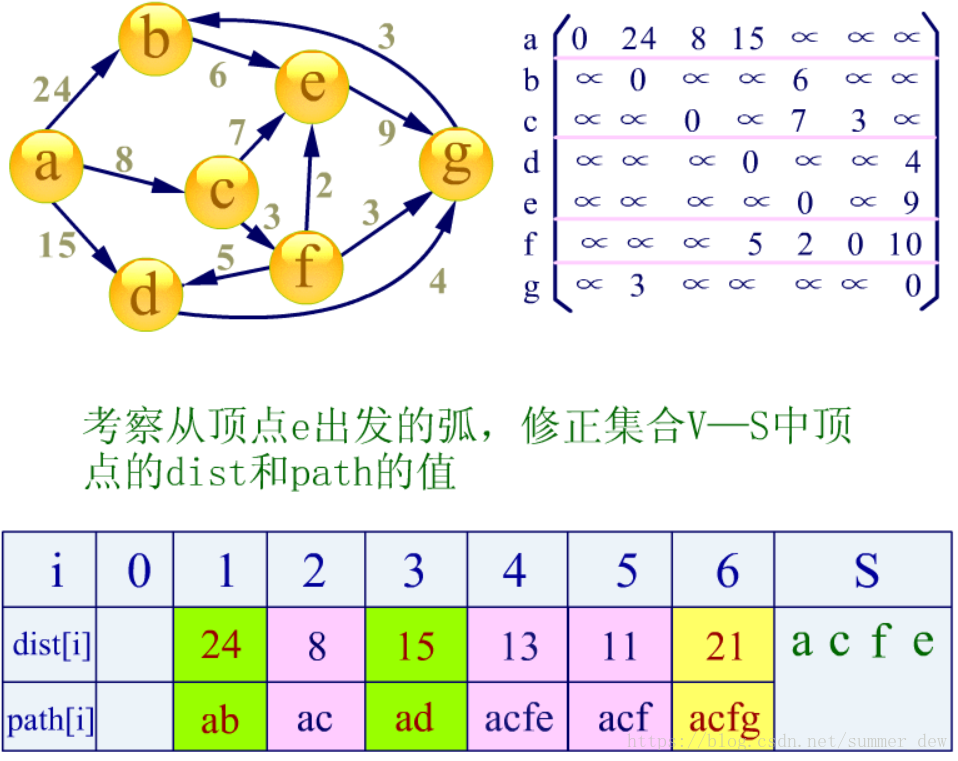
【步骤五】 

 

 

【步骤六】

 

 

 

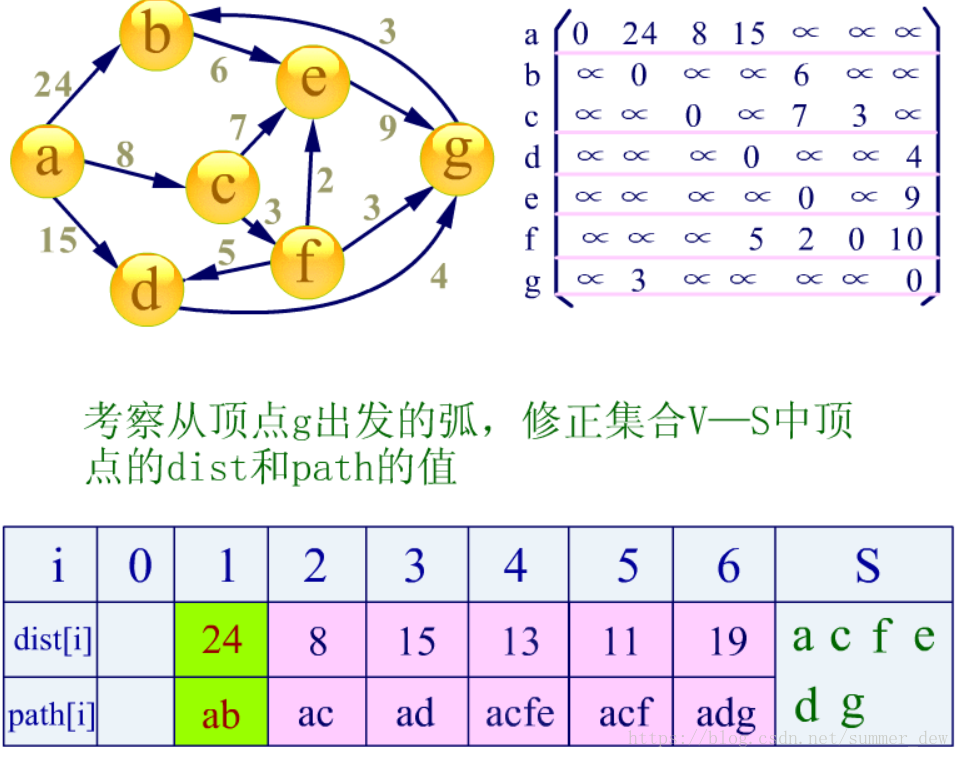
【算法结束】

1. dist[v]：起点0到v的最短路径长度
2. path[v]：起点0到v的最短路径

 

 

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <stdbool.h>
#include <stdlib.h>
#include <stack>

#define INF 0x3f3f3f3f
using namespace std;
const int MAXN = 10005;

int graph[MAXN][MAXN];
int dist[MAXN];
bool vis[MAXN];
int pre[MAXN];
int n,m;

stack<int> path;

void dijistra(int x){
    int pos = x;
    memset(pre,-1, sizeof(pre));
    for(int i = 1; i <= n; i ++){
        dist[i] = graph[pos][i];
    }
    vis[pos] = true;
    for(int i = 1; i <= n; i ++){
        int mins = INF;
        for(int j = 1; j <= n; j ++){
            if(!vis[j] && dist[j] < mins){
                pos = j;
                mins = dist[j];
            }
        }
        vis[pos] = true;
        for(int j = 1; j <= n; j ++){
            if(!vis[j] && dist[j] > dist[pos] + graph[pos][j]){
                dist[j] = dist[pos] + graph[pos][j];
                pre[j] = pos;
            }
        }
    }
}

int main()
{
    freopen("../in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d",&n,&m);
        for (int i=1;i<=n;i++)
        {
            for (int j=1;j<=n;j++)
            {
                if (i == j)
                    graph[i][j] = 0;
                else
                    graph[i][j] = INF;
            }
        }
        for (int i=1;i<=m;i++)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            graph[a][b] = graph[b][a] = c;
        }

        int start,end;
        scanf("%d%d",&start,&end);
        memset(vis, false, sizeof(vis));
        dijistra(start);
        int temp = end;
        while (pre[temp]!=-1)
        {
            path.push(temp);
            temp = pre[temp];
        }
        path.push(temp);
        cout << "path: " << start << " ";
        while (!path.empty())
        {
            printf("%d ",path.top());
            path.pop();
        }
        cout << endl;
        cout << "distance:" << endl;
        printf("%d\n",dist[end]);
    }
    return 0;
}

 

上面的是数组的写法，但是有的时候题目的数据量太大往往会导致数组的写法不能够使用。

因为不能够开这么大的数组，嘤嘤嘤

 

所以现在重点来了，我们使用邻接矩阵的写法并且采取优先队列的方式对我们Dj算法进行优化：

 

模版题： poj1511：http://poj.org/problem?id=1511

#include <stdio.h>
#include <algorithm>
#include <iostream>
#include <stdbool.h>
#include <stdlib.h>
#include <string>
#include <string.h>
#include <math.h>
#include <vector>
#include <queue>
#include <stack>
#include <map>

#define INF 0x3f3f3f3f
#define LL long long
#define MAXN 1000001
using namespace std;

typedef pair<int,int> P;  //first 是最短距离，second 是编号
struct edge{     // 边
    int f;  // 起点
    int t;  // 终点
    int c;  // 花费
    edge(){
        f = 0;
        t = 0;
        c = 0;
    }
    edge(int ff,int tt,int cc){
        f = ff;
        t = tt;
        c = cc;
    }
};
int n,m;
int dist[MAXN];  // 记录距离
vector<edge> graph[MAXN];  // 领接矩阵
edge edges[MAXN];  // 存边的数组
bool vis[MAXN];

void dijkstra(int x)
{
    priority_queue<P,vector<P>,greater<P> > Q;
    for (int i=1;i<=n;i++)
        dist[i] = INF;
    dist[x] = 0;
    memset(vis,false, sizeof(vis));
    Q.push(P(0,x));
    while (!Q.empty())
    {
        int v = Q.top().second;
        Q.pop();
        if (vis[v])  //如果更新过
            continue;
        vis[v] = true;
        // 遍历当前点相邻的所有点
        for (int i=0;i<graph[v].size();i++)
        {
            edge e = graph[v][i];
            if (dist[e.t]>dist[v]+e.c) //找最短路
            {
                dist[e.t] = dist[v] + e.c;
                Q.push(P(dist[e.t],e.t));
            }
        }
    }
}

void init()
{
    for (int i=0;i<=n;i++)
        graph[i].clear();
}


int main()
{
    //freopen("../in.txt","r",stdin);
    int T;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d",&n,&m);
        init();
        for (int i=1;i<=m;i++)
        {
            int a,b,c;
            scanf("%d %d %d",&a,&b,&c);
            edges[i] = edge(a,b,c);
            graph[a].push_back(edge(a,b,c)); // a 为顶点
            //graph[b].push_back(edge(b,a,c));  无向图
        }
        dijkstra(1);
        long long int sum = 0;
        for (int i=1;i<=n;i++)
            sum += dist[i];
        init();
        for (int i=1;i<=m;i++)
        {
            edge tmp = edges[i];
            graph[tmp.t].push_back(edge(tmp.t,tmp.f,tmp.c));
        }
        dijkstra(1);
        for (int i=1;i<=n;i++)
            sum += dist[i];
        printf("%lld\n",sum);
    }
    return 0;
}

 

前向星加链式存储加优先队列优化

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <stdlib.h>
#include <queue>

#define INF 0x3f3f3f3f
#define pii pair<int,int>
using namespace std;
const int MAXN = 2e5+7;

int head[MAXN];
int dist[MAXN];
bool vis[MAXN];
int cnt;

struct Edge{
    int to,val,next;
}edge[MAXN];

void init(){
    cnt = 0;
    memset(head,-1, sizeof(head));
    memset(vis,false, sizeof(vis));
    memset(dist,INF, sizeof(dist));
}

void add(int u,int v,int w){
    edge[cnt].to = v;
    edge[cnt].val = w;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

void dijstra(int s)
{
    priority_queue<pii,vector<pii>,greater<pii> > q;
    dist[s] = 0;
    q.push({dist[s],s});
    while (!q.empty())
    {
        int now = q.top().second;
        q.pop();
        if (vis[now])
            continue;
        vis[now] = true;
        for (int i=head[now];i!=-1;i=edge[i].next)
        {
            int v = edge[i].to;
            if (dist[v]>dist[now]+edge[i].val)
            {
                dist[v] = dist[now] + edge[i].val;
                q.push({dist[v],v});
            }
        }
    }
}

int main()
{
    int n,m,s;
    while (~scanf("%d%d",&n,&m))
    {
        init();
        while (m--)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            add(a,b,c);
        }
        dijstra(1);
        printf("%d\n",dist[n]);
    }
    return 0;
}