群论学习笔记
定义：
若集合 \(G \ne \varnothing\)，在 \(G\) 上的二元运算（该运算称为群的乘法，注意它未必是通常意义下数的乘法，其结果称为积）\(·:G·G\longrightarrow G\) 构成的代数结构 \((G,·)\)，满足：
-
封闭性：即G的任意两个元素在 下的运算结果都是该集合的一个元素。（\(\forall a,b\in G\),\(a·b \in G\))；
-
结合律：\(\forall a,b,c \in G\)，有 \(a·(b·c)=(a·b)·c\)；
-
单位元：\(G\) 中存在元素 \(e\)，使 \(G\) 中任意元素 \(e\) 与之相乘的结果都等于 \(a\) 本身。（ \(\exists e \in G\)，使 \(\forall a \in G\)，有 \(e·a=a·e=a\)）；
-
逆元：\(\forall a \in G\) ，\(\exists b \in G\) ，使得 \(a·b=b·a=e\)(\(e\) 即为单位元)，\(b\) 称为 \(a\) 的逆元，记为 \(a^{-1}\)，
则称为一个群,同为乘法群。
在无歧义时，可将 a·b写成 ab。
性质：
-
单位元是唯一的，例如乘法的单位元是 1，加法的是 0。
-
任意一个元素的逆元是唯一的
-
\(\forall a,b \in G\)，方程 \(ax=b\),\(ay=b\)，在 \(G\) 中都有解\(x=a^{-1}b,y=ba^{-1}\)
-
\(\forall a,b,c\in G\) 若 \(ab=ac\) 则 \(b=c\),若 \(ba=ca\) 则 \(b=c\)。
-
任意一个元素的逆元的逆元是其本身
-
\(\forall a,b\in G\),\((ab)^{-1}=b^{-1}·a^{-1}\)
置换群：
通俗的说，置换群是指与群 \(G\) 所同构的所有群，最多有 \(n!\) 种，此时即为群 \(G\) 的全排列。
交换群：
满足交换律的群，称为交换群。
群的历史起源，就是伽罗瓦galois和阿贝尔abel在考虑多项式方程的根之间的对称性时形成最初的变换雏形的。
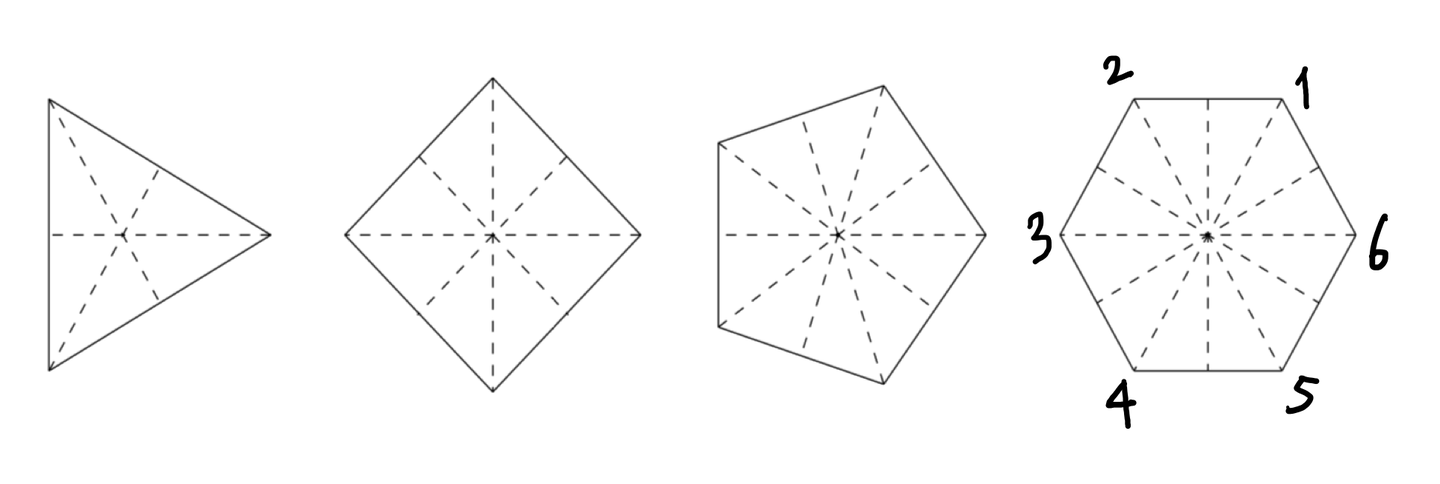
考虑根的对称性，其实就是考虑正多边形的变换群。
因为 ，在复平面上画出来正好就是正n边形的n个顶点。
这些保持正多边形不变的几何变换的全体刚好构成一个群，而且元素为2n个。
拿正六边形来说，就是12个，如图中所示。
这里分为两类，一类是旋转有n个，一类是翻折也是n个，即轴对称翻转。
对应到上述图中，旋转就是虚线终点在顶点上的那n个，而翻折就是虚线终点在边中点的那n个。
同构实际上是一个非常广泛和普遍的概念。
其主旨是说两个事物在某种程度或者某种意义上可以看成一个事物。
其实同构的概念是天然和分类的思想相互关联的。
我们努力学习同构的概念，很大的原因就是为了分类。
最容易理解的例子就是我们初中学习的三角形的全等。
三角形的全等其实就是一种同构。
由于我们关心的是三角形的数学上(其实就是逻辑上的)量，即三个角和三条边，这六个要素。
而不关心你在黑板上画出来的三角形是红色还是白色，线条的粗细等。
因此，在数学上一个很自然的想法，关于两个三角形是否一样(即同构或者全等)，就产生了。
如果两个三角形的上述六个要素(三个角度三条边长度)相对应的相等，则我们称这两个三角形全等(即同构，或者说相等的意思)。
显然六个要素都对应相等的话，两个三角形就能通过移动而重合了。
这也很符合我们的直观感受。
于是就有了好几个判定全等的定理。
可见，如何定义同构，是有我们的目的以及一些隐含的必然逻辑在的。
比如上述三角形全等的定义，是因为如此定义的两个全等的三角形在后续的数学研究中起到的作用是完全一样的。
不会说两个全等的三角形，它们的面积或者周长却不相等。
回到我们的正题，我们来定义两个群的同构。
就像三角形的全等定义一样，我们应该先搞清楚一个群有哪些要素。
很明显它有两个要素，首先一个群是一个集合，其次它上面有乘法运算结构。
我们只要让两个群的上述两个要素都对应相同就可。
两个集合，仅仅作为集合，我们只要他们的个数一样多即可。
即两个集合间存在双射(就是一一对应)。
于是我们有了两个群同构的严格定义如下：
当 \((G,*)\)与 \((H,\hearts）\)同构
\(f(a*b)=f(a)\hearts f(b)\),\(\forall a,b \in G\)
正规子群
如果群G的子群H(\(H \lhd G\))，满足如下条件
\(xhx^{-1}\in H,\forall x \in G,h\in H\)
则我们称H是G的一个正规子群。
可解群是概念有关五次以上多项式方程无根式解的证明过程中的一个至关重要的概念。
包括它的名字的由来，大家想想，「可解」的意思就是指的方程「可解」。
如果有限群G存在如下的一个子群序列：
\({(1)}\lhd H_1 \lhd H2...\lhd H_n =G\)
其中前一个是后一个的正规子群，且后一个的阶数是前一个素数倍，
则我们称群G是可解群。
域也是一个集合，然后上面有两种运算，我们通常称为加法和乘法。
每个单独的运算加上集合本身构成一个很不错的代数结构，
比如域与其加法构成一个交换群。
两个运算之间又有很好的兼容性，
比如分配率
我们最熟悉的域的例子其实一直都在我们身边，那就是有理数域，实数域，复数域
因此我们讲域的时候，根本就不需要抽象的定义，就是数的通常的加法和乘法。
我们可以直接用如下的方式来定义数域。
数域的定义
我们称复数集的一个子集为数域，如果该子集对加减乘除封闭的话。
这个很好理解，它就是指两个域作为集合，大的包含小的，那么大的就称为小的扩域。
比如实数域就是有理数域的扩域。
我们通常用记号 K\F,表示K是F的扩域，或者说从F到K是一个域的扩张。记系数域为F, 多项式f在数域F上的分裂域K是F的一个扩域。
小插曲：被从首页撤下来了，疑似没有和程序员相关的东西，但马上就要有了。
因为想上首页必须要有和程序员相关的东西，所以暂停写伽罗瓦定理的计划，我们先开始走进 Pólya。
引入例题
Pólya 定理在计数方面可以统计「本质不同」的方案个数。
生动形象的表述，就是有一件有 \(n\) 面的物体，给其每一面染色，求其「本质不同」的方案个数。
而「本质不同」可以有各种定义。
Pólya 定理和 Burnside 引理类似。但我们的问题细化一些：
我们给 \(S\) 中每一个元素染色，统计 \(T\) 作用下本质不同的染色方案数。
已经介绍轮换的概念，记 c(g) 为 g 中的轮换个数，N 为颜色集合。
则有：\(|S/T| = \frac 1{|T|}\sum_{g\in T}|N|^{c(g)}\)。
其中 \(|N|^{c(g)}=|S|^g\)
