推荐系统基础
评测指标
预测准确度
评分预测
预测用户对物品的评分
\({r_{ui}}\) = 用户u对物品i的实际评分
\({\hat r_{ui}}\) = 推荐系统给出的预测评分
RMSE(均方根误差)
MAE(平均绝对误差)
假设列表records存放用户评分数据,令records[i] = [u,i,rui,pui]
rui = 用户u对物品i的实际评分
pui = 算法预测用户u对物品i的评分
RMSE和MAE的代码实现:
def RMSE(records):
return math.sqrt(
sum([(rui - pui) * (rui - pui) for u, i, rui, pui in records]) / float(len(records))
)
def MAE(records):
return sum([abs(rui-pui) for u, i, rui, pui in records]) / float(len(records))
若评分系统是基于整数建立的,那么对预测结果取整将降低MAE的误差
TopN推荐
给用户一个个性化的推荐列表,一般预测准确度通过 precision / recall 度量
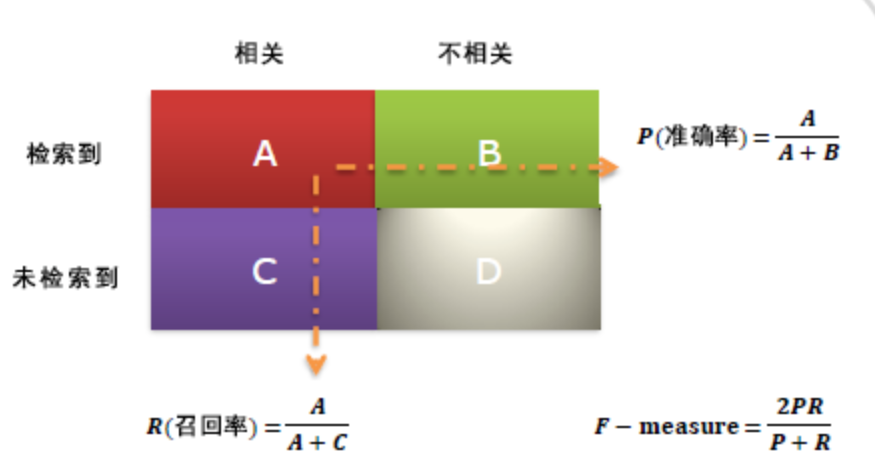
召回率(recall)
准确率(precision)
R(u) = 根据用户在训练集上的行为给用户作出的推荐列表
T(u) = 用户在测试集上的行为列表
def PrecisionRecell(test, N): # precision and recall
hit = 0
n_recall = 0
n_precision = 0
for user, items in test.items():
rank = Recommand(user, N)
hit += len(rank & items)
n_recall += len(items)
n_precision += N
return [hit / (1.0 * n_recall), hit / (1.0 * n_precision)]
def Recall(train, test, N):
hit = 0
all = 0
for user in train.keys():
tu = test[user]
rank = GetRecommendation(user,N)
for item, pui in rank:
if item in tu:
hit += 1
all += len(tu)
return hit / (all * 1.0)
def Precision(train, test, N):
hit = 0
all = 0
for user in train.keys():
tu = test[user]
rank = GetRecommendation(user,N)
for item, pui in rank:
if item in tu:
hit += 1
all += N
return hit / (all * 1.0)
覆盖率
推荐系统对长尾的发掘能力
流行度计算
a(i) = 物品i被推荐的次数
T = 所有物品被推荐的次数
流行度与覆盖率是此消彼长的
推荐物品占总物品集合的比例
U = 用户集合
R(u) = 推荐系统给每个用户推荐的长度为N的物品列表
一个好的推荐系统不仅需要有比较高的用户满意度,也要有比较高的覆盖率
但这种方法太过于粗略,可以研究物品在推荐列表中出现次数的分布描述推荐系统发掘长尾的能力
信息熵
p(i) = 物品流行度除以所有物品流行度之和
基尼系数
\(i_j\) = 按照物品流行度p()从小到大排序的物品列表中的第j个物品
n = len(p)
基尼系数与系统物品流行度分布均匀情况成反比
多样性
描述推荐列表中物品两两之间的不相关性
\(s(i,j)\in [0,1]\) = 物品i与物品j的相识度
用户u的推荐列表R(u)的多样性:
系统整体多样性可定义为所有用户推荐列表多样性的平均值:
新颖性
评测新颖度的最简单方法就是利用推荐结果的平均流行度,因为越不热门的物品越可能让用户觉得新颖
def Popularity(train, test, N):
# 训练集中每个物品出现的次数, 即出现在了多少个用户中
item_popularity = dict()
for user, items in train.items():
for item in items:
if item not in item_popularity:
item_popularity[item] = 0
item_popularity[item] += 1
# 物品在训练集中出现的次数
ret = 0
# 所有商品在推荐列表中出现的总次数
n = 0
for user in train.keys():
rank = GetRecommendation(user, N)
for item, pui in rank:
# 取对数,防止因长尾问题带来的被流行物品所主导
ret += math.log(1 + item_popularity.get(item, 0))
n += 1
# 物品出现的次数 除以 总的物品数
ret /= n*1.0
return ret
惊喜度
惊喜度(serendipity),注意与新颖度的区别
如果推荐结果和用户的历史兴趣不相似,但却能让用户觉得满意
信任度
增加推荐系统透明度\(\to\)提供推荐解释\(\to\)用好友进行解释
…
协同过滤
实验设计
数据集:使用ml-1m
将行为数据均匀分布成M份,取一份为测试集,M-1份为训练集,为了保证评测指标不是过拟合的结果,需要进行M次实验,并且每次使用不同的数据集,最后求出M次评测指标的平均值
def SplitData(data, M, k, seed):
test = []
train = []
random.seed(seed)
for user, item in data:
# 注意:由于random.randint(0,M)的取值范围是[0,M],这里取M-1
if random.randint(0, M-1) == k:
test.append([user, item])
else:
train.append([user, item])
return train, test
评测指标:准确率 / 召回率
覆盖率:使用最简单的覆盖率定义
新颖度:如上
基于领域的算法
基于用户的协同过滤算法
步骤:
- 找到和目标用户兴趣相似的用户集合
- 找到这集合中的用户喜欢,且将目标用户没有听说过的物品推荐给目标用户
相似度计算
N(u) = 用户u曾经有过正反馈的物品集合
N(v) = 用户v曾经有过正反馈的物品集合
Jaccard公式:
余弦相似度:
def UserSimilarity1(train):
# 时间复杂度n*n
W = dict()
for u in train.keys():
W[u] = dict()
for v in train.keys():
if u == v:
continue
W[u][v] = len(train[u] & train[v])
W[u][v] /= math.sqrt(len(train[u]) * len(train[v]) * 1.0)
return W
该方法在用户数很大时非常耗时,事实上很多用户之间并没有对同样的物品产生过行为,所以上述代码很多时候将时间浪费在了\(\lvert N(u)\cap N(v) \rvert = 0\)上面
改进方法:可以首先计算出\(\lvert N(u)\cap N(v) \rvert \not= 0\)的用户对(u,v),并建立用户-物品倒排表,再计算。
def UserSimilarity2(train):
# 改进的计算方法
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i in items:
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
# calculate co-related items between users
C = dict() # 用户之间的相似物品数
N = dict() # 每个用户的物品数
for i, users in item_users.items():
for u in users:
if u not in N:
N[u] = 0
N[u] += 1
C[u] = dict()
for v in users:
if u == v:
continue
if v not in C[u]:
C[u][v] = 0
C[u][v] += 1
# calculate finnial similarity matrix W
W = dict()
for u, related_users in C.items():
W[u] = dict()
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return W
John S. Breese在论文中提出的方法:
该公式通过\(\frac{1}{\log1+\lvert N(i) \rvert}\)惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响
def UserSimilarity3(train):
"""
改进的计算方法, 相似度惩罚
"""
# build inverse table for item_users
item_users = dict()
for u, items in train.items():
for i in items.keys():
if i not in item_users:
item_users[i] = set()
item_users[i].add(u)
# calculate co-related items between users
C = dict() # 用户之间的相似物品数
N = dict() # 每个用户的物品数
for i, users in item_users.items():
for u in users:
N[u] += 1
for v in users:
if u == v:
continue
C[u][v] += 1 / math.log(1 + len(users))
# calculate finnial similarity matrix W
W = dict()
for u, related_users in C.items():
for v, cuv in related_users.items():
W[u][v] = cuv / math.sqrt(N[u] * N[v])
return W
UserCF推荐算法
在得到用户之间的兴趣相似度后,UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的物品
度量UserCF中用户u对物品i的感兴趣程度:
\(S(u,K)\) = 包含和用户u兴趣最接近的K个用户
\(N(i)\)= 对物品i有过行为的用户集合
\(w_{uv}\) = 用户u和用户v的兴趣相似度
\(r_{vi}\) = 用户v对物品i的兴趣(因为使用的是单一行为的隐反馈数据,所以所有的\(r_{vi}\) = 1)
def Recommend(user, train, W):
rank = dict()
interacted_items = train[user]
for v, wuv in train[v].items():
if i in interacted_items[v].items():
#we should filter items user interacted before
continue
rank[i] += wuv * rvi
return rank