基础数论
质数: 在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数
合数:在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数
约数(因数) :能够将一个数整除的数
质因数:能够将一个数整除的质数
互质:公约数只有1的两个整数
质数
质数:在大于1的整数中,如果只包含1和本身两个约数,就被称为质数或者叫素数
素数的判定
- 试除法 (O(\(\sqrt{n}\)))
若\(d \mid n\)存在,则\(\frac{n}{d} \mid n\)一定存在,所以约数都是成对出现的,所以枚举中可以只枚举小的哪一个,即\(d \leq \frac{n}{d} \rightarrow d \leq \sqrt{n}\)
而在使用中考虑到sqrt()的速度问题和i * i的溢出问题,故用i <= n / i这种写法
if (n < 2) return false;
for (int i = 2; i <= n / i; i++) {
if (n % i == 0) return false;
}
return true;
2. kn + i法 (O(\(n^{\frac{1}{3}}\)))
一个大于1的整数如果不是素数,那么一定有素因子,因此在枚举因子时只需要考虑可能为素数的因子即可。 kn + i法即枚举形如kn + i的数,例如取k = 6,那么6n + 3, 6n +4, 6n + 6都不可能为素数(显然它们分别有因子2,3,,2,6一定不是素数),因此我们只需要枚举形如6n + 1, 6n +5的数即可
k = 30的模板:
bool isPrime(LL n) {
if (n == 2 || n == 3 || n == 5) return 1;
if (n % 2 == 0 || n % 3 == 0 || n % 5 == 0 || n == 1) return 0;
LL c = 7, a[8] = {4, 2, 4, 2, 4, 6, 2, 6};
while (c * c <= n) for (auto i : a){if (n % c == 0) return 0; c += i;}
return 1;
}
- Miller - Rabin 判定法(大素数测试算法)(O(\(k\log{n}\)))
对于一个很大的数 (例如十进制表示有100位),如果还是采用试除法进行判定,时间复杂度必定难以承受,目前比较稳定的大素数测试算法是米勒-拉宾素数测试算法,该素数测试算法可以通过控制迭代次数来间接控制正确率
Miller - Rabin 判定法是基于费马小定理的,即如果一个数 为素数的条件是对于所有和 互素的正整数 满足以下等式:\(a^{p-1} \equiv 1 \ (mod\ p)\)
然而我们不可能试遍所有和p互素的正整数,这样的话复杂度反而更高,事实上我们只需要取比p小的几个素数进行测试就行了,一般是10个
模板
// 快速幂
ll qpow(ll a, ll b, ll q)
{
ll res = 1; //因为是用乘法模拟乘方,所以res要是1
while (b)
{
if (b & 1)
res = (res * a) % q;
a = (a * a) % q; //视情况将 * 换成Mul(龟速乘)
b >>= 1;
}
return res % q;
}
/************************************************/
ll Rand()
{ //决定了程序的性能
static ll x = (srand((int)time(0)), rand());
x += 1000003;
if (x > 1000000007)
x -= 1000000007;
return x;
}
bool Witness(ll a, ll n)
{
ll t = 0, u = n - 1;
while (!(u & 1))
u >>= 1, t++;
ll x = qpow(a, u, n), y; // qpow为快速幂
while (t--)
{
y = x * x % n;
if (y == 1 && x != 1 && x != n - 1)
return true;
x = y;
}
return x != 1;
}
bool MillerRabin(ll n, ll s) // s一般取10
{
if (n == 2 || n == 3 || n == 5)
return 1;
if (n % 2 == 0 || n % 3 == 0 || n % 5 == 0 || n == 1)
return 0;
while (s--)
{
if (Witness(Rand() % (n - 1) + 1, n))
return false;
}
return true;
}
筛质数
- 埃氏筛 (O(\(n \log{\log{n}}\)))
const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N]; // flast 质数, true 合数
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = i;
for (int j = i + i; j <= n; j += i) st[j] = true;
}
}
时间复杂度推理:
1~n中有\(\frac{n}{\ln{n}}\)个质数,所以原本要算\(n(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})=n\ln{n}\)次,现在只需要算\(\frac{n\ln{n}}{\ln{n}} \to n\log{\log{n}}\)次(粗略估计)
- 线性筛(欧拉筛)(O(n))
const int N = 1e6 + 10;
int primes[N], cnt;
bool st[N]; // flast 质素, true 合数
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i;
for (int j = 0; primes[j] <= n / i; j++) {// 从小到大枚举所有质数
st[primes[j] * i] = true;
if (i % primes[j] == 0) break; // 避免重复标记
}
}
前提:n只会被最小质因子筛掉,线性筛保证每个合数都会被它的最小质因子筛掉
i % primes[j] == 0时primes[j]一定是i的最小质因子,因为是从小到大枚举的,primes[j]一定是primes[j]*i的最小质因子
i % primes[j] != 0时primes[j]一定小于i的所有质因子,primes[j]也一定是primes[j]*i的最小质因子
所以无论如何primes[j]一定是primes[j]*i的最小质因子,primes[j]*i一定是合数
对于一个合数x假设primes[j]是x的最小质因子,当i枚举到x / primes[j]的时候就筛掉,我们用最小质因子来筛,每个数都只有一个最小质因子,所以是线性的
反素数
任何小于n的数的正约数个数都小于n的正约数个数,即n是1…n中正约数个数最多的数
素数就是因子只有两个的数,那么反素数,就是因子最多的数(并且因子个数相同的时候值最小)
分解质因数
- 试除法 (O(\(\sqrt{n}\)))
方法:枚举所有数,分解质因子,优化:n中最多只包含一个大于sqrt(n)的质因子
for (int i = 2; i <= n / i; i++) {
if (n % i == 0) { // i一定是质数
int s = 0;
while (n % i == 0) {
n /= i;
s++;
}
printf("%d %d\n", i, s);
}
}
if (n > 1) printf("%d %d\n", n, 1);
约数
试除法求一个数的所有约数 (O(\(\sqrt{n}\)))
若\(d \mid n\)存在,则\(\frac{n}{d} \mid n\)一定存在,所以约数都是成对出现的,所以枚举中可以只枚举小的哪一个再通过\(\frac{n}{d}\)得到另一个
vector<int> res;
for (int i = 1; i <= n / i; i++) {
if (n % i == 0) {
res.push_back(i);
if (i != n / i) res.push_back(n / i);// 有可能 n = i ^ 2 避免重复
}
}
sort(res.begin(), res.end());
约数个数
唯一分解定理:任何一个大于1的数都可以被分解成为有限个质素乘积的形式
\(N=p_1^{C_1} \times p_2^{C_2} \times \cdots \times p_m^{C_m} = \prod_{i=1}^mp_i^{C^i}\)
其中\(p_1 < p_2 < \cdots < p_m\)为质数,\(C_i\) 为正整数
\(N\)的正约数个数为:
\((c_1+1)\times(c_2+1)\times\cdots(c_m+1)=\prod_{i=1}^m(c_i+1)\)
unordered_map<int, int> primes;
long long res = 1;
while (n--) {
int x;
cin >> x;
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
x /= i;
primes[i]++;
}
}
if (x > 1) primes[x]++;
}
for (auto prime : primes) res = res * (prime.secind + 1);
\(N^M\)的正约数个数为:
\((M \times c_1+1)\times(M \times c_2+1)\times\cdots(M \times c_m+1)=\prod_{i=1}^m(M \times c_i+1)\)
约数之和
同理,\(N\)的所有正约数和为:
\((1+p_1+p_1^2+\cdots+p_1^{c_1})\times\cdots\times(1+p_m+p_m^2+\cdots+p_m^{c_m})=\prod_{i=1}^m(\sum_{j=0}^{c_i}(p_i)^j)\)
unordered_map<int, int> primes;
long long res = 1;
while (n--) {
int x;
cin >> x;
for (int i = 2; i <= x / i; i++) {
while (x % i == 0) {
x /= i;
primes[i]++;
}
}
if (x > 1) primes[x]++;
}
for (auto prime : primes) {
int p = prime.first, a = prime.second; // p是底数 a是指数
LL t = 1;
while (a--) t = (t * p + 1) % mod;//(p * (p + 1) + 1) = p^2 + p + 1
res = res * t % mod;
}
最大公约数
- 辗转相除法(欧几里得算法)O(\(\log{n}\))
\(\forall a,b\in\mathbb{N},b\neq0,\gcd(a,b)=\gcd(b,a\bmod b)\)
int gcd(int a, int b){
return b ? gcd(b, a % b) : a;
}
-
更相减损术
-
二进制gcd
int gcd(int a,int b)
{
if(a==b) return a;//a=b
if(!a) return b;//a=0
if(!b) return a;//b=0
if(~a&1)//a是偶数
{
if(b&1)//b是奇数
return gcd(a>>1,b);
else//b是偶数
return gcd(a>>1,b>>1)<<1;
}
if(~b&1)//a是奇数b是偶数
return gcd(a,b>>1);
//均为奇数
if(a>b) return gcd((a-b)>>1,b);
return gcd((b-a)>>1,a);
}
第K大公约数
先求出a和b的gcd,a和b的公约数一定也是最大公约数的约数,所以求第K大公约数,可以从1到gcd枚举k个,用gcd除以第k小个约数便是第k大个约数
LL t = gcd(a, b);
for (i = 1; i < t / i; i++) {
if (a % i == 0 && b % i == 0) cnt++;
if (cnt >= k) break;
}
cout << t / i << endl;
倍数
最小公倍数 = 两数之积除以最大公约数
欧拉函数
符号: \(\varphi(n)\) 定义:1~n中互质的数的个数
证明(容斥原理):
- 从\(1~N\)中去掉\(p_1,p_2,\cdots p_k\)的所有倍数
- 加上\(p_i*p_j\)的倍数
- 减去所有\(p_i*p_j*p_k\)的倍数
int res = a;
for (int i = 2; i <= a / i; i++) {
if (a % i == 0) {
res = res / i * (i - 1); // res * (1 - 1 / a) 避免除法
while (a % i == 0) a /= i;
}
}
if (a > 1) res = res / a * (a - 1);
若一个数是质素,其欧拉函数:\(\varphi(p) = p \times (1 - \frac{1}{p}) = p - 1\)
筛法求欧拉函数
typedef long long LL;
const int N = 1e6 + 10;
int primes[N], cnt;
int phi[N];
bool st[N];
LL get_eulers(int n) {
phi[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) {
primes[cnt++] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
if (i % primes[j] == 0) {
phi[primes[j] * i] = phi[i] * primes[j];
break;
}
phi[primes[j] * i] = phi[i] * (primes[j] - 1);
}
}
LL res = 0;
for (int i = 1; i <= n; i++) res += phi[i];
return res;
}
欧拉定理:
若a与n互质,则有
费马小定理:
若p是质数,则有
快速幂
在\(O(\log k)\)下求出\(a^k \mod p\)的结果
int qmi(int a, int k, int p) {
int res = 1;
while (k) {
if (k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
快速幂求逆元
前提:p为质数
由费马小定理知:在p为质数的情况下,\(a^{p-1}(mod\quad p)\)的变形为:\(a\times a^{p-2}(mod\quad p)\)
则\(a^{p-2}(mod\quad p)\)就是逆元
int inv(int x,int p) {return qmi(x, p - 2, p) % p;}
int res = inv(a, p);
if (a % p) printf("%d\n", res);
else puts("impossible");
扩展欧几里得算法
当\(b = 0\)时\(ax+by=a\)故而\(x=1,y=0\)
当\(b \not= 0\)时
由欧几里得算法:\(gcd(a,b)=gcd(b,a\%b)\)
裴蜀定理:对于任意整数a,b,一定存在整数x,y,使得\(ax+by=gcd(a,b)\)
故由裴蜀定理:
可以用递归算法,先求出下一层的X1,y1,再回代到上一层,层层回代,可求特解\((x_0,y_0)\)
扩展欧几里得算法的目的就是得到x,y,gcd
int exgcd(int a, int b, int &x, int &y) {
if (!b) {
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
求解线性同余方程
给定\(n\)组数据\(a_i,b_i,m_i\),对于每组数求出一个\(x_i\),使其满足$a_i \times x_i \equiv b_i\ (mod\ m_i) $
-
把同余方程转化为不定方程
由$ax \equiv b\ (mod\ m) \(,得\)ax = m(-y)+b\(,即\)ax+my=b$
由裴蜀定理知:当\(gcd(a,m)\mid b\)时有解
-
用扩欧算法求\(ax + my = gcd(a, m)\)的解把\(x\)乘以\(b/gcd(a, m)\)即得原方程的特解
int a, b, m, x, y;
scanf("%d%d%d", &a, &b, &m);
int d = exgcd(a, m, x, y);
if (b % d) puts("impossible");
else printf("%d\n", (LL)x * (b / d) % m);
扩展欧几里得求逆元
前提:a与p互质
\(ax \equiv 1\ (mod\ p)\)
- 将乘法逆元转化为不定方程,等价变形\(ax+py = 1\)
- 扩展欧几里得求\(ax + py = gcd(a,p)\)的解\(x\),\((x\%p+p)\%p\)即答案
int a, p, x, y;
cin >> a >> p;
exgcd(a, p, x, y);
cout << (x % p + p) % p << endl;
中国剩余定理
计算求解线性同余方程
其中模数\(m_1,m_2,\dots m_n\)为两两互质的整数,求x的最小非负整数解
- 计算所有模的乘积
- 计算第i个方程的\(c_i=\frac{M}{m_i}\)
- 计算\(c_i\)在模\(m_i\)意义下的逆元\(c_{i}^{-1}\)
- \(x=\sum_{i=1}^{n}r_ic_ic_{i}^{-1}\)
模板\(O(nlog{c})\)
LL CRT(LL m[], LLr[]) {
LL m = 1, ans = 0;
for (int i = 1; i <= n; i++) M *= m[i];
for (int i = 1; i <= n; i++) {
LL c = M / m[i], x, y;
exgcd(c, m[i], x, y);
ans = (ans + r[i] * c * x % M) % M;
}
return (ans % M + M) % M;
}
高斯消元
高斯消元解线性方程组
在\(O(n^3)\)的时间复杂度内求解包含\(n\)个方程和\(n\)个未知数的多元线性方程
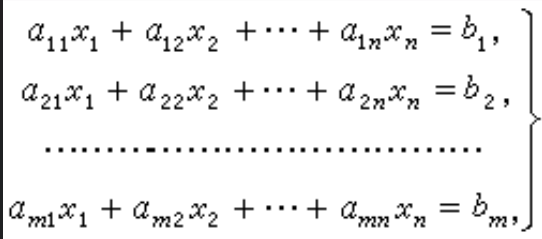
通过初等行变换转化为行最简形矩阵
枚举每一列c
- 找到绝对值最大的一行
- 将该行换到最上面
- 将该行的第1个数变成1
- 将下面所有的第c列消成0
每次循环排到最上面的那一行不参与下次循环
解的判定:
上三角矩阵行数对于n:有唯一解(完美消成上三角矩阵)
上三角矩阵行数小于n :
-
有矛盾(0 = C):无解
-
没矛盾(0 = 0):无穷多解
模板:
const int N = 110;
const double eps = 1e-6; // 考虑计算机中除法精度,只要小于eps就算为0
int n;
double a[N][N];
/*************************************/
int gauss() {
int c, r;
for (c = 0, r = 0; c < n; c++) {
int t = r;
for (int i = r; i < n; i++) {
if (fabs(a[i][c]) > fabs(a[t][c])) {
t = i;
}
}
if (fabs(a[t][c]) < esp) continue;
for (int i = c; i <= n; i++) swap(a[t][i], a[r][i]);
for (int i = n; i >= c; i--) a[r][i] /= a[r][c];
for (int i = r + 1; i < n; i++) {
if (fabs(a[i][c]) > esp) {
for (int j = n; j >= c; j--) {
a[i][j] -= a[r][j] * a[i][c];
}
}
}
r++;
}
if (r < n) {
for (int i = r; i < n; i++) {
if (fabs(a[i][n]) > esp) return 2; // 无解
}
return 1; // 有无穷多解
}
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 1; j < n; j++) {
a[i][n] -= a[i][j] * a[j][n];
}
}
return 0; // 有唯一解
}
组合数
$C_{a}^{b} = \frac{a!}{b!(a-b)!} $
递推式:
\(C_{a}^{b} = C_{a-1}^{b} + C_{a-1}^{b-1}\)
递推组合数
(小范围(2000)内可用)\(O(n^2)\)
void init() {
for (int i = 0; i < N; i++) {
for (int j = 0; j <= i; j++) {
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
}
预处理阶乘和逆元的阶乘
(较大范围(\(10^5\))可用)\(O(n\log n)\)
$C_{a}^{b} = \frac{a!}{b!(a-b)!} $
先预处理出阶乘和逆元的阶乘,再由(LL)fact[a] * infact[a - b] % mod * infact[b] % mod的到组合数
const int N = 100010, mod = 1e9 + 7;
typedef long long LL;
int fact[N], infact[N];
/************************************/
fact[0] = infact[0] = 1;
for (int i= 1; i < N; i++) {
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
卢卡斯定理
大组合数问题(巨大范围(\(10^{18}\))可用)\(O(p\log N \log p)\)
前提:p为质数(\(1 \leq p \leq 10^5\))
\(C_{n}^{m} \equiv C_{n\mod p}^{m \mod p} \times C_{n/p}^{m/p}\ (mod\ p)\)
\(C_{n/p}^{m/p}\)可以继续用卢卡斯定理求解
边界条件:当\(m = 0\)时,返回1
int C(int a, int b) {
int res = 1;
for (int i = 1, j = a; i <= b; i++, j--) {
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2) % p;
}
return res;
}
int lucas(LL a, LL b) {
if (a < p && b < p) return C(a, b);
return (LL)C(a % p, b % p) * lucas(a / p, b / p) % p;
}
高精度组合数
(不取模)
$a! = \lfloor \frac{a}{p} \rfloor + \lfloor \frac{a}{p^2} \rfloor + \lfloor \frac{a}{p^3} \rfloor \dots $
typedef long long LL;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n) {
// 线性筛
}
int get(int n, int p) {
int res = 0;
while (n) {
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> &A, int b) {
// 高精度乘低精度
}
int main() {
int a, b;
cin >> a >> b;
get_primes(a);
for (int i = 0; i < cnt; i++) {
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p); //
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i++) {
for (int j = 0; j < sum[i]; j++) {
res = mul(res, primes[i]);
}
}
for (int i = res.size() - 1; i >= 0; i--) printf("%d", res[i]);
return 0;
}
卡特兰数
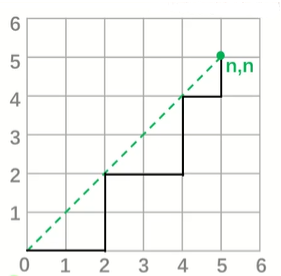
以走网格为例,从点(0,0)走到格点(n,n),只能向右或向上走,并且不能越过对角线的路径的条数,就是卡特兰数
通项公式:
特征:
向上走的步数不能超过向右走的步数,即一种操作数不能超过另一种操作数,或两种操作不能有交集
例:
- 一个有n个0和n个1组成的字串,且所有的前缀字串皆满足1的个数不超过0的个数。这样的字串个数有多少?
- 包含n组括号的合法运算式的个数有多少?
这些都需要在任意前缀中满足一个操作数恒大于等于另一个操作数
P1044 NOIP2003 普及组 栈 - 洛谷
像这道题合法的操作数就需要满足在任意前缀中进栈数量大于出栈数量,直接卡特兰数解决
容斥原理
集合的并
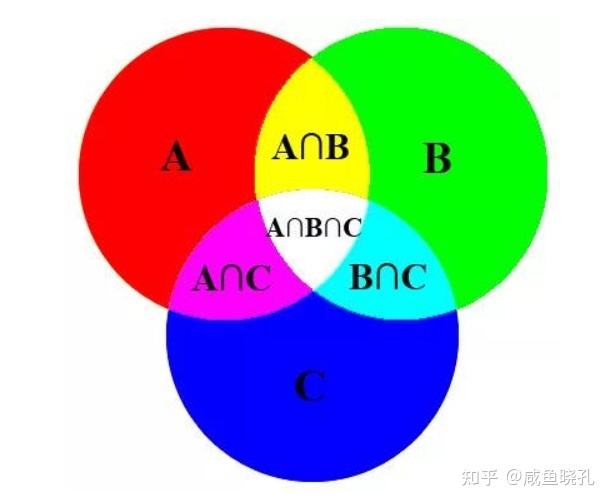
$图面面积 = S_A+S_B+S_C-S_A\cap S_B-S_C\cap S_C-S_B\cap S_C+S_A\cap S_B\cap S_C $
故有:
时间复杂度:\(O(2^n)\)
规律:奇加偶减,所以集合的并\(\cup\) = 集合的交\(\cap\)的交错和
- 集合的大小:
集合的大小等于n除以质素的乘积的下取整,即
- 二进制位枚举
使用二进制位来表示每个集合选与不选的状态,若有三个质数则需要三个二进制位来表示所有状态\[001 \to S_1 \quad 010 \to S_2 \quad 100 \to S_3 \\ 011 \to S_1 \cap S_2 \quad 101 \to S_! \cap S_3 \quad 011 \to S_2 \cap S_3 \\ 111 \to S_1 \cap S_2 \cap S_3 \]只需要枚举001到111的每个状态就可以计算出交集的交错和
typedef long long LL;
const int N = 20;
int n, m, prim[N];
int calc() { // 容斥原理
int res = 0;
for (int i = 1; i < 1 << m; i++) { // 枚举状态
int t = 1; sign = -1;
for (int j = 0; j < m; j++) { // 过滤状态
if (i & 1 << j) {
if ((LL)t * prim[j] > n) {
t = 0; break;
}
t *= prim[j]; // 质数的积
sign = -sign;
}
}
if (t) res += n / t * sign; // 交集的和
}
return res;
}
其中第一个for中i < 1 << m:
若m为3,枚举\(001 \to 111\)的每个状态,则\(i < (1 << m = 1000)\)
第二个for中i & 1 << j:
判断当前状态下选着了那些:\(101 \to S_1 \cap S_2\)
\(当j = 0时,101\ \&\ (1 << j = 001) = 1\)
\(当j = 1时,101\ \&\ (1 << j = 010) = 0\)
\(当j = 2时,101\ \&\ (1 << j = 100) = 1\)
集合的交
集合的交等于全集减去补集的并
补集的并使用容斥原理计算
在没有给出每个集合而是给出了每个集合的补集和全集的情况下使用
例:知$U = {1,2,3,4,5,6,7,8},\ \overline{A} = {3,4,6,8},\ \overline{B} = {1,4,6,7,8},\ 求\vert A\cap B \vert $
博弈论
先手必败状态:可以走到某一个必败状态
先手必胜状态:走不到任何一个必败状态
NIM游戏
异或和为0则先手必败,异或和不为0则先手必胜
而如果先手必胜应该如何取石子呢?
先手为必胜态则后手必为必败态,即后手的石子异或和为0,设原异或和为\(X\)
运用异或结合律(以\(a_2\)举例)
那么将\((a_2\oplus X)\)视为新的一堆石子,\(a_2 - (a_2\oplus X)\)即为需要取走的数量
这里要注意\((a_2\oplus X)\)必须小于\(a_2\), 且异或运算优先级很低,要加括号
公平组合游戏
若一个游戏满足:
- 由两名玩家交替行动
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关
- 不能行动的玩家判负
NIM博弈属于公平组合游戏,但城建的棋类游戏,比如围棋就不是公平组合游戏,因为围棋双方只能落黑子和白子,胜负的判定也比较复杂,不满足条件2和条件3
有向图游戏
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子,两名玩家交替的把这枚棋子沿有向边进行移动,每次可以移动一步,无法移动者判负
任何一个公平组合游戏都可以转换成为有向图游戏,将每个局面看成图中的一个节点,并且从每个局面向着合法行动能够到达的下一个局面连有向边
Mex运算
设S表示一个非负整数集合,定义\(mex(S)\)为求出不属于集合S的最小非负整数的运算,即:\(mex(S) = min\{x\}\),s属于自然数,且x不属于S
SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点\(y_1, y_2...y_k\),定义\(SG(x)\)为x的后继节点\(y_1,y_2\dots y_k\)的\(SG\)函数值构成的集合再执行\(mex(S)\)运算的结果,即:
\(SG(x) = mex(SG(y_1),SG(y_2)\dots SG(Y_k))\)
特别地。整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即\(SG(G)=SG(s)\)


