后缀数组入门

后缀数组的定义:

后缀数组 (Suffix Array) 指某个字符串的所有后缀按字典排序后得到的数组。数组中只保存后缀开始的位置。简称SA。

后缀：从某个字符串的某个开始位置到其末尾的字符串子串,包括原串和空字符串。

例子：{ABC}的后缀{ABC},{BC},{C},{}

字典排序: 默认从小到大

构造后缀数组:

朴素做法：将n个字符串进行sort排序,时间复杂度\(O(n^2log_2n)\)
倍增数组法: Manber和Myers发明,需要进行 \(log_2n\) 次排序,排序时间复杂度 \(O(nlog_2n)\) ,所以总时间复杂度是 \(O(nlog_2^2n)\) ,可以用基数排序将sort排序进行优化,总时间复杂度优化成 \(O(nlog_2n)\)。
所以一般来说,倍增数组的方法够用了,更快的可以去找[SA-IS 算法]或者[DC3算法]

倍增数组法的代码:

步骤:

开始以长度为1的后缀字符串为排序规则对其SA进行排序,并求出其排名Rank(蓝色区域)
以长度k的后缀字符串的Rank为排序规则对SA排序,求出长度为2k的后缀字符串的排序结果.并求出长度为2k的Rank.原因:长度为2k的后缀字符串的rank总能由长度为k的后缀字符串的rank求出(绿色区域->绿色区域)
重复步骤2 直到构造出完整的SA。

(图：以之前的Rank构造新的Rank的过程)

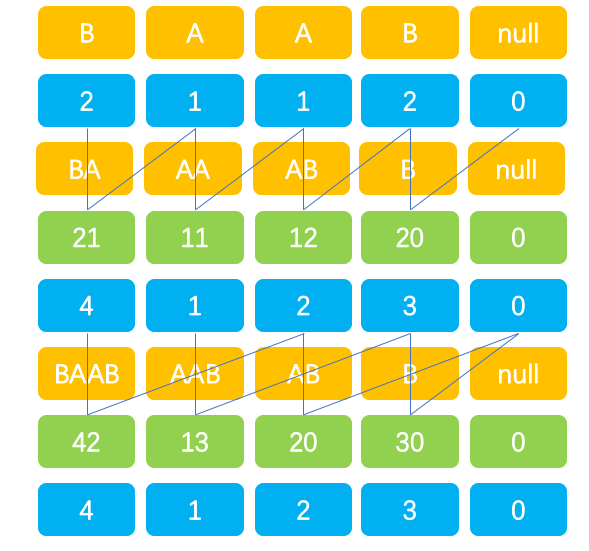
下面给出用未优化后的代码。

未优化代码(点击展开)

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000
using namespace std;

char str[MAXN];//字符串数组
int sa[MAXN + 1];//后缀数组,+1是为了存储(空字符串)
int rank[MAXN + 1];//Rank[i]第i位开始的子串排名(0~N)
int tmp[MAXN+1];
int k,n;

bool cmp_sa(const int &i,const int &j) {
	if(rank[i] != rank[j])	return rank[i]<rank[j];
	else {
	/**由先前的rank求出现在的rank,
	比如{AB} 要由{A}和{B}的rank一起求出,因为{A}和{B}是连在一起并且{AB}的长度是{B}的2k倍,所以加上长度k就可以求出{B}的rank**/
		int l = i+k<=n?rank[i+k]:-1;
		int r = j+k<=n?rank[j+k]:-1;
		return l<r;
	}
}

void build_sa(const char* str,int *sa) {
	n = strlen(str);
	//长度为1的sa,rank取编码,因为空字符串排最前,这里取-1
	for(int i=0; i<=n; i++) {
		sa[i] = i;
		rank[i] = rank[i] < n? str[i]:-1;
	}
	//倍增思想
	for(k=1; k<n; k*=2) {
		//对sa进行排序,也是对长度为2*k的后缀字符串进行排序
		sort(sa,sa+n+1,cmp_sa);
		tmp[sa[0]] = 0;
		for(int i=1; i<=n; i++) {//计算新的rank
			tmp[sa[i]] = tmp[sa[i-1]] + (cmp_sa(sa[i-1],sa[i])?1:0);
		}
		for(int i=0; i<=n; i++) {
			rank[i] = tmp[i];
		}
	}
}

int main() {
	scanf("%s",&str);
	build_sa(str,sa);
	return 0;
}

优化:

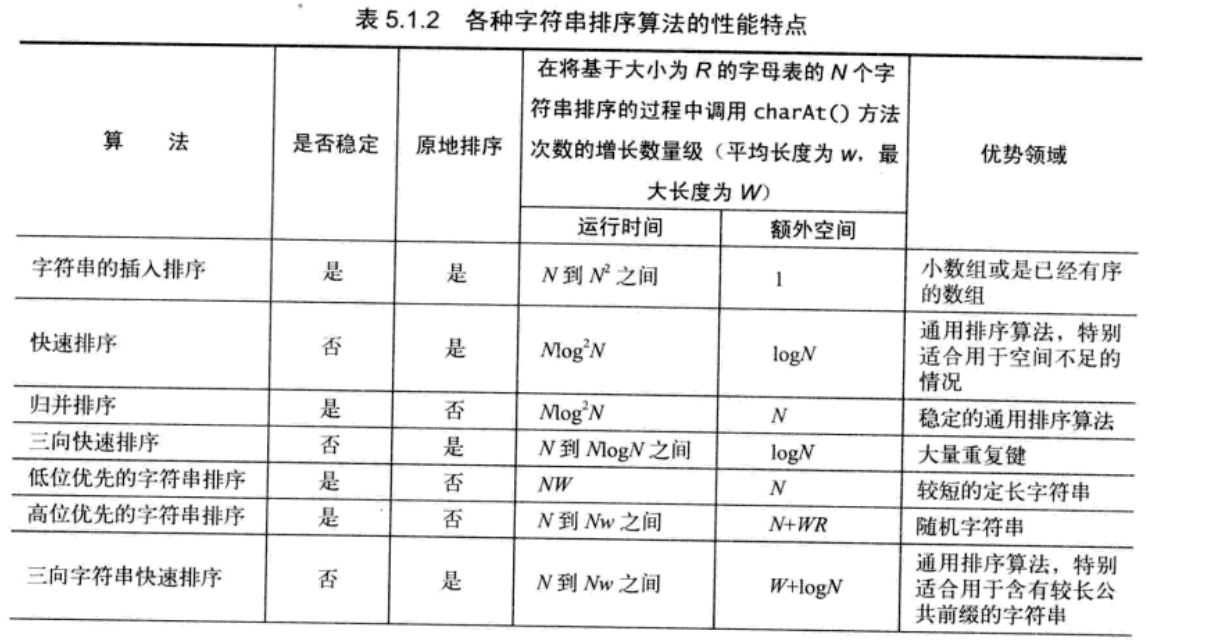
可以看出影响我们的算法复杂度的主要因素是字符串的排序算法。为了优化我们的算法,我们得选择一些更快的排序方法。为了与网上大多数后缀数组模板统一,这里我们选择LSD基数排序,也就是表中的低位字符串排序作为替代品。

先介绍几个概念

基数排序:从各级关键字的最低有效位开始依次进行稳定排序(计数排序,桶排序等等具有稳定性的排序)。由于可能存在多级关键字，所以基数排序分为LSD(least significant digit)和MSD(most significant digit)

计数排序可以作为基数排序的一个子过程。

以二位整数位为例子,介绍下LSD基数排序,因为每位数只有0_{9这10个数字,那么我们需要构造10个桶(0}9),然后开始选取关键字，那就是各位上的数字，根据数的个位数上的数，十位数的数，将二位整数依次放入0~9的桶中。

图:序列{11,83,81,21,63} 通过LSD基数排序变为 {11,21,63,83}

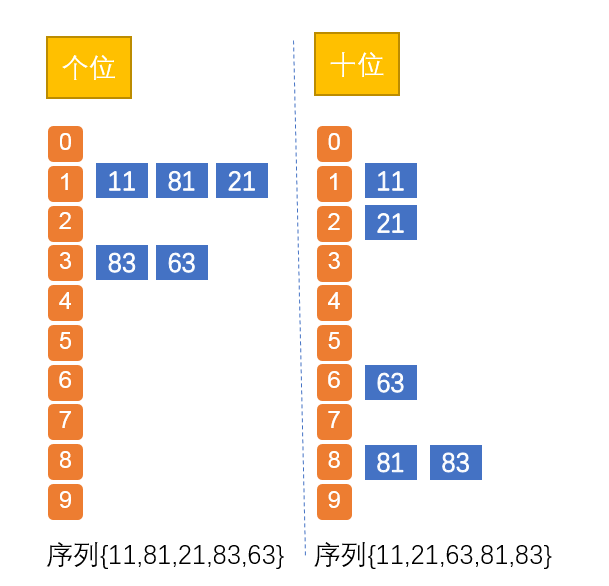
这只是LSD基数排序的原理而已。

要将基数排序运用到字符串上还需要一些小改变。具体可以参考《算法》第四版的 5.1 字符串排序章节。

优化代码(点击展开)

//参考代码
//https://codeforces.com/contest/1037/submission/42406942
//https://codeforces.com/contest/1037/submission/42965008
#include <cstdio>
#include <string>
#include <algorithm>
#include <cctype>
#include <cstring>

#define MAXN 1000010
#define MAXM 127

using namespace std;

char str[MAXN]; //字符串数组
int c[MAXN]; //计数排序的桶
int RA[MAXN],tempRA[MAXN];
int SA[MAXN],tempSA[MAXN];

void count_sort(int k,int n,int m) {
	for(int i=0; i<m; i++) c[i]=0;
	//第一次循环,ABCAB字符串中,最后一个字符没有第二部分,所以优先级最高 
	for(int i=0; i<n; i++) ++c[i+k<n?RA[i+k]:0];
	for(int i=1; i<m; i++) c[i]+=c[i-1];
	//根据之前的结果求出新的Sa数组 
	for(int i=n-1; i>=0; i--) tempSA[--c[SA[i]+k<n?RA[SA[i]+k]:0]]=SA[i];
	for(int i=0; i<n; i++) SA[i] = tempSA[i];
}

void get_sa(const char* str) {//m表示排序字符串最大ASCII值,也就是桶最大容量 
	int n=strlen(str),m,q;
	m = max(MAXM,n);
	for(int i=0; i<n; i++) RA[i]=str[i]; //初始化Rank
	for(int i=0; i<n; i++) SA[i] = i;
	//进行多次基数排序
	for(int k=1; k<n; k<<=1) {
		//根据{AB}字符串的{B}部分进行SA进行计数排序,在根据{A}部分进行一次.
		//基数排序原理:年月日的话，就各对日，月，年进行一次稳定排序.
		count_sort(k,n,m);
		count_sort(0,n,m);
		//计算Rank
		tempRA[SA[0]] = q = 0;
		//用旧的Rank算出新的Rank(倍增原理)
		//第一次循环 ABCAB => 
		// 	    Rank{02301}
		for(int i=1; i<n; i++) tempRA[SA[i]] = (RA[SA[i]]==RA[SA[i-1]]&&RA[SA[i]+k]==RA[SA[i-1]+k]?q:++q);
		for(int i=0; i<n; i++) RA[i] = tempRA[i];
		if(q==n-1) break;//优化,每个桶的元素个数 <= 1,就不用继续排序了
		m=q+1;//优化,减少桶的数量
	}
	for(int i=0;i<n;i++) printf("%d ",SA[i]+1);
}

int main() {
	scanf("%s",&str);
	get_sa(str);
	return 0;
}

//abracadabra

未注释压缩核心代码

#include <cstdio>
#include <string>
#include <algorithm>
#include <cctype>
#include <cstring>
#define MAXN 1000010
#define MAXM 127

using namespace std;

char str[MAXN];
int c[MAXN];
int RA[MAXN],tempRA[MAXN];
int SA[MAXN],tempSA[MAXN];

void count_sort(int k,int n,int m) {
	for(int i=0; i<m; i++) c[i]=0;
	for(int i=0; i<n; i++) ++c[i+k<n?RA[i+k]:0];
	for(int i=1; i<m; i++) c[i]+=c[i-1];
	for(int i=n-1; i>=0; i--) tempSA[--c[SA[i]+k<n?RA[SA[i]+k]:0]]=SA[i];
	for(int i=0; i<n; i++) SA[i] = tempSA[i];
}

inline void get_sa(const char* str) {
	int n=strlen(str),m;
	m = max(MAXM,n);
	for(int i=0; i<n; i++) RA[SA[i] = i]=str[i];
	for(int k=1,q; k<n; k<<=1,m=q+1) {
		count_sort(k,n,m);
		count_sort(0,n,m);
		tempRA[SA[0]] = q = 0;
		for(int i=1; i<n; i++) tempRA[SA[i]] = (RA[SA[i]]==RA[SA[i-1]]&&RA[SA[i]+k]==RA[SA[i-1]+k]?q:++q);
		for(int i=0; i<n; i++) RA[i] = tempRA[i];
		if (q == n - 1) break;
	}
	for(int i=0; i<n; i++) printf("%d ",SA[i]+1);
}

int main() {
	scanf("%s",str);
	get_sa(str);
	return 0;
}

应用:

字符串匹配:

求字符串T在字符串S中出现的位置,通过二分搜索就可以在 \(O(|T|log_2|S|)\) 时间内完成,适合 \(|S|\) 字符串较长的情况。

int contain(string S,string T){
	int l=0,r=S.length()-1;
	while(l<=r){
		int mid = (r+l)/2;
		//以sa[mid]为下标开始,长度为T.length()的字符串S与字符串T比较的结果
		int re = S.compare(sa[mid],T.length(),T);
		if(re<0) l=mid+1;
		else if(re>0)r=mid-1;
		else return sa[mid];
	}
	return -1;
}

高度数组(LCP Array,Longest Common Prefix Array):

(PS:等我补完多校再说)

题目:

Best Cow Line(数据加强版)
POJ3581

参考博客和文献:

https://www.cnblogs.com/jinkun113/p/4743694.html
https://www.cnblogs.com/victorique/p/8480093.html

挑战程序设计竞赛（第2版）《算法》第四版《算法导论》

https://www.geeksforgeeks.org/suffix-array-set-2-a-nlognlogn-algorithm/

posted @ 2019-07-07 00:40 zz2108828 阅读(485) 评论(0) 编辑收藏举报

刷新页面返回顶部

(ﾟДﾟ≡ﾟдﾟ)!? (°∀°)ﾉ欢迎光临Σ(ﾟдﾟ;)