动态规划 树形DP (最大连续子序列和 与 树上DP) 洛谷P1122

 动态规划 树形DP (最大连续子序列和 与 树上DP) 洛谷P1122

 

题目描述
小明对数学饱有兴趣，并且是个勤奋好学的学生，总是在课后留在教室向老师请教一些问题。一天他早晨骑车去上课，路上见到一个老伯正在修剪花花草草，顿时想到了一个有关修剪花卉的问题。于是当日课后，小明就向老师提出了这个问题：

一株奇怪的花卉，上面共连有N N朵花，共有N-1N−1条枝干将花儿连在一起，并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”，该数越大说明这朵花越漂亮，也有“美丽指数”为负数的，说明这朵花看着都让人恶心。所谓“修剪”，意为：去掉其中的一条枝条，这样一株花就成了两株，扔掉其中一株。经过一系列“修剪“之后，还剩下最后一株花（也可能是一朵）。老师的任务就是：通过一系列“修剪”（也可以什么“修剪”都不进行），使剩下的那株（那朵）花卉上所有花朵的“美丽指数”之和最大。

老师想了一会儿，给出了正解。小明见问题被轻易攻破，相当不爽，于是又拿来问你。

输入输出格式
输入格式：
第一行一个整数N(1 ≤ N ≤ 16000)N(1≤N≤16000)。表示原始的那株花卉上共N N朵花。

第二行有N N个整数，第II个整数表示第II朵花的美丽指数。

接下来N-1N−1行每行两个整数a,ba,b，表示存在一条连接第aa 朵花和第bb朵花的枝条。

输出格式：
一个数，表示一系列“修剪”之后所能得到的“美丽指数”之和的最大值。保证绝对值不超过21474836472147483647。

输入输出样例
输入样例#1： 
7
-1 -1 -1 1 1 1 0
1 4
2 5
3 6
4 7
5 7
6 7
输出样例#1： 
3
说明
【数据规模与约定】

对于60\%60%的数据，有N≤1000N≤1000；

对于100\%100%的数据，有N≤16000N≤16000。

 

这题用了 树上DP + 最大连续子序列和题目。

 

 

假设我们从 -2 结点 开始搜索,为了方便表示，用结点值代表结点编号

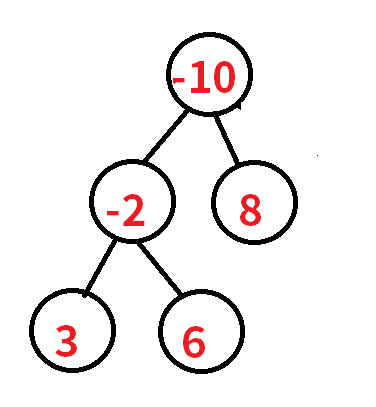
用DP{i} 记录取以i为根的子树最大的收益是多少的最大值。

以 -2结点 作为子树序列的尾(根)，叶结点 3,-10,8 作为子树序列的头部 (叶)

那么就有 3个 以-2结尾的子树序列 {-2,-10,8} {-2,3} {-2,6},这三个子树序列共同构成了以 - 2 为根的子树

以序列① {8,10,-2}  开始，

dp{8}  = 8, ( 8作为结尾)

dp[-10} = 8 + (-10) = -2

dp{-2} = -2 (因为 dp{-10} < 0 )

以序列② {3,-2}  开始，

dp{3} = 3,

dp{-2} = 3 + dp{-2} = 1

以序列② {3,-2}  开始，

dp{6} = 6

dp{-2} = 6 + dp {-2} =  6 + 1 = 7

求出 每个结点dp值 的最大值就是答案了。

DP思想:

　　用DP{i} 记录取以i为根的子树最大的收益是多少的最大值。

#include <iostream>
#include <algorithm>
#include <vector> 
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 1;
vector<vector<int> > node(N,vector<int>());
int v[N],vis[N];
int dp[N];
int n;
int ans;

void dfs(int u,int fa){//u表示当前结点，fa表示父结点 
    dp[u] = v[u];
    for(int i=0;i<node[u].size();++i){
        int v = node[u][i];
        if(v != fa){//避免回到父结点 
            dfs(v,u);
            if(dp[v] > 0){
                dp[u] += dp[v];
            }
        }
    }
}

int main(){
    ios::sync_with_stdio(false);
     
    cin >> n;
    int a,b;
    for(int i=1;i<=n;++i){
        cin >> v[i];
    }
    for(int i=1;i<=n-1;++i){
        cin >> a >> b;
        node[a].push_back(b);
        node[b].push_back(a);
    }
    
    dfs(1,0);
    ans = -INF;
    for(int i=1;i<=n;++i){
        ans = max(ans,dp[i]);
    }
    cout << ans << endl;
    return 0;
}