HDU 3507斜率优化dp
Print Article
Time Limit: 9000/3000 MS (Java/Others) Memory Limit: 131072/65536 K (Java/Others)
Total Submission(s): 12185 Accepted Submission(s): 3733
Problem Description
Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
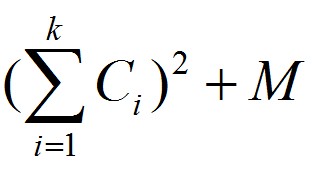
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost
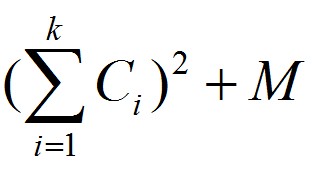
M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
Input
There are many test cases. For each test case, There are two numbers N and M in the first line (0 ≤ n ≤ 500000, 0 ≤ M ≤ 1000). Then, there are N numbers in the next 2 to N + 1 lines. Input are terminated by EOF.
Output
A single number, meaning the mininum cost to print the article.
Sample Input
5 5
5
9
5
7
5
Sample Output
230
Author
Xnozero
Source
题意:
有n个字,每个字有权值a[i],要打印第j到第i之间的字要花费sum(a[i]~a[j])+m的费用,求最少花费。
输入n,m
输入n个数的a[i]
代码:
//和上一个题一样,dp[i]=min(dp[j]+m+(sum[i]-sum[j])^2) #include<iostream> #include<cstdio> #include<cstring> using namespace std; typedef long long ll; const int inf=0x3f3f3f3f; const int maxn=500009; int n,m,que[maxn]; ll sum[maxn],dp[maxn]; ll getdp(int i,int j){ return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]); } ll getup(int j,int k){ return dp[j]-dp[k]+sum[j]*sum[j]-sum[k]*sum[k]; } ll getlow(int j,int k){ return 2*(sum[j]-sum[k]); } int main() { while(scanf("%d%d",&n,&m)==2){ sum[0]=0; for(int i=1;i<=n;i++){ scanf("%lld",&sum[i]); sum[i]+=sum[i-1]; } int head=0,tail=0; que[tail++]=0; for(int i=1;i<=n;i++){ while(head+1<tail&&getup(que[head+1],que[head])<sum[i]*getlow(que[head+1],que[head])) head++; dp[i]=getdp(i,que[head]); while(head+1<tail&&getup(que[tail-1],que[tail-2])*getlow(i,que[tail-1])>=getup(i,que[tail-1])*getlow(que[tail-1],que[tail-2])) tail--; que[tail++]=i; } printf("%lld\n",dp[n]); } return 0; }



