Codeforces Round #202 (Div. 2) B,C,D,E
Igor has fallen in love with Tanya. Now Igor wants to show his feelings and write a number on the fence opposite to Tanya's house. Igor thinks that the larger the number is, the more chance to win Tanya's heart he has.
Unfortunately, Igor could only get v liters of paint. He did the math and concluded that digit d requires ad liters of paint. Besides, Igor heard that Tanya doesn't like zeroes. That's why Igor won't use them in his number.
Help Igor find the maximum number he can write on the fence.
The first line contains a positive integer v (0 ≤ v ≤ 106). The second line contains nine positive integers a1, a2, ..., a9 (1 ≤ ai ≤ 105).
Print the maximum number Igor can write on the fence. If he has too little paint for any digit (so, he cannot write anything), print -1.
5
5 4 3 2 1 2 3 4 5
55555
2
9 11 1 12 5 8 9 10 6
33
0
1 1 1 1 1 1 1 1 1
-1
题意:
有v克油漆,可以写1~9九个数字,其中给出每个数字耗费的油漆量,问用这些油漆能写出的最大数字是多少。
代码:
//简单的贪心。显然能够写的数字位数越多就越大,其次是数字的字面值尽量大。 //最多能写多少位数字,找到最小的那个,求出剩余油漆,然后从大到小枚举数字, //看看能否换上这个数字,能换几个,换了之后更新剩余油漆。 #include<bits/stdc++.h> using namespace std; const int inf=0x7fffffff; int n,v,a[1000006],ans[1000006]; int main() { cin>>v; int mini,minn=inf; for(int i=1;i<=9;i++){ cin>>a[i]; if(a[i]<minn){ minn=a[i]; mini=i; } } int maxn=v/a[mini]; int vv=v%a[mini]; queue<int>q; for(int i=1;i<=maxn;i++) q.push(mini); if(maxn>0){ for(int i=9;i>=1;i--){ int sum=vv,tmp=0; for(int j=1;j<=maxn;j++){ if(q.front()>i) break; sum+=a[q.front()]; if(sum<j*a[i]){ sum-=a[q.front()]; break; } q.pop();tmp=j; } if(tmp) vv=sum%a[i]; while(tmp--) q.push(i); } } if(maxn==0) cout<<"-1\n"; else{ int cnt=0; while(!q.empty()){ ans[cnt++]=q.front();q.pop(); } sort(ans,ans+cnt); for(int i=cnt-1;i>=0;i--) cout<<ans[i]; cout<<endl; } return 0; }
One day n friends gathered together to play "Mafia". During each round of the game some player must be the supervisor and other n - 1people take part in the game. For each person we know in how many rounds he wants to be a player, not the supervisor: the i-th person wants to play ai rounds. What is the minimum number of rounds of the "Mafia" game they need to play to let each person play at least as many rounds as they want?
The first line contains integer n (3 ≤ n ≤ 105). The second line contains n space-separated integers a1, a2, ..., an (1 ≤ ai ≤ 109) — the i-th number in the list is the number of rounds the i-th person wants to play.
In a single line print a single integer — the minimum number of game rounds the friends need to let the i-th person play at least ai rounds.
Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64dspecifier.
3
3 2 2
4
4
2 2 2 2
3
You don't need to know the rules of "Mafia" to solve this problem. If you're curious, it's a game Russia got from the Soviet times: http://en.wikipedia.org/wiki/Mafia_(party_game).
题意:
有n个人玩游戏,每局游戏都要有一个人不能参与,给出每个人希望自己玩的次数,问满足所有人的情况下最少玩几局。
代码:
//设最少要玩x局。则x>=max(a[i])(1<=i<=n),(x-a[1])+(x-a[2])+...+(a-a[n])>=x; //得到 x>=sum/(n-1).然后取max(x,max(a[i])); #include<bits/stdc++.h> using namespace std; int n,a[100005]; int main() { scanf("%d",&n); double sum=0; for(int i=0;i<n;i++){ scanf("%d",&a[i]); sum+=a[i]; } sort(a,a+n); int x=ceil(sum/(double)(n-1)); x=max(x,a[n-1]); printf("%d\n",x); return 0; }
DFS
You are given a rooted tree with n vertices. In each leaf vertex there's a single integer — the number of apples in this vertex.
The weight of a subtree is the sum of all numbers in this subtree leaves. For instance, the weight of a subtree that corresponds to some leaf is the number written in the leaf.
A tree is balanced if for every vertex v of the tree all its subtrees, corresponding to the children of vertex v, are of equal weight.
Count the minimum number of apples that you need to remove from the tree (specifically, from some of its leaves) in order to make the tree balanced. Notice that you can always achieve the goal by just removing all apples.
The first line contains integer n (2 ≤ n ≤ 105), showing the number of vertices in the tree. The next line contains n integers a1, a2, ..., an(0 ≤ ai ≤ 108), ai is the number of apples in the vertex number i. The number of apples in non-leaf vertices is guaranteed to be zero.
Then follow n - 1 lines, describing the tree edges. Each line contains a pair of integers xi, yi (1 ≤ xi, yi ≤ n, xi ≠ yi) — the vertices connected by an edge.
The vertices are indexed from 1 to n. Vertex 1 is the root.
Print a single integer — the minimum number of apples to remove in order to make the tree balanced.
Please, do not write the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the sin, cout streams cin, cout or the %I64d specifier.
6
0 0 12 13 5 6
1 2
1 3
1 4
2 5
2 6
6
题意:
n个节点的树,每个节点有若干的苹果,要想使每个节点的子分支都有相同数量的苹果,最少要去掉多少苹果。
代码:
//假设根节点有三个儿子,每个儿子又分别有2,3,4个儿子,如果每个孙子节点上都有 //苹果那么三个儿子分别至少要分2,3,4个苹果才能够分给孙子,又要满足分支苹果相等的条件, //可以取他们的最小公倍数,每个儿子分12个苹果(如果苹果数足够)。 //dfs计算每一层每个分支的苹果总数sum[i],每一个节点有多少个分支cnt[i],取cnt[i]的最小公 //倍数lcm,这一层每个分支应该拥有的苹果数m是取最小的一个sum[i]->m=sum[i]-sum[i]%lcm。 //即让m是lcm的倍数并且每个分支都至少能够提供m个苹果。最终递归到根节点就是满足条件的苹果数。 #include<bits/stdc++.h> using namespace std; typedef long long ll; int n,a[200005]; ll sum[200005],cnt[200005]; vector<int>g[200005]; ll gcd(ll a,ll b) { return b?gcd(b,a%b):a; } ll lcm(ll a,ll b) { return a/gcd(a,b)*b; } void dfs(int u,int fa) { int next=0; for(int i=0;i<(int)g[u].size();i++){ int v=g[u][i]; if(v==fa) continue; dfs(v,u); if(!next){ sum[u]=sum[v]; cnt[u]=cnt[v]; } else{ if(cnt[u]<5e13) cnt[u]=lcm(cnt[u],cnt[v]); sum[u]=min(sum[u],sum[v])/cnt[u]*cnt[u]; } next++; } if(!next){ sum[u]=a[u];cnt[u]=1; } else{ sum[u]*=next; if(cnt[u]<5e13) cnt[u]*=next; } } int main() { scanf("%d",&n); ll ans=0; for(int i=1;i<=n;i++){ scanf("%d",&a[i]); ans+=a[i]; } int x,y; for(int i=1;i<n;i++){ scanf("%d%d",&x,&y); g[x].push_back(y); g[y].push_back(x); } dfs(1,0); printf("%I64d\n",ans-sum[1]); return 0; }
数据结构
You are given an array a1, a2, ..., an and m sets S1, S2, ..., Sm of indices of elements of this array. Let's denote Sk = {Sk, i} (1 ≤ i ≤ |Sk|). In other words, Sk, i is some element from set Sk.
In this problem you have to answer q queries of the two types:
- Find the sum of elements with indices from set Sk:
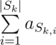 . The query format is "? k".
. The query format is "? k". - Add number x to all elements at indices from set Sk: aSk, i is replaced by aSk, i + x for all i (1 ≤ i ≤ |Sk|). The query format is "+ k x".
After each first type query print the required sum.
The first line contains integers n, m, q (1 ≤ n, m, q ≤ 105). The second line contains n integers a1, a2, ..., an (|ai| ≤ 108) — elements of array a.
Each of the following m lines describes one set of indices. The k-th line first contains a positive integer, representing the number of elements in set (|Sk|), then follow |Sk| distinct integers Sk, 1, Sk, 2, ..., Sk, |Sk| (1 ≤ Sk, i ≤ n) — elements of set Sk.
The next q lines contain queries. Each query looks like either "? k" or "+ k x" and sits on a single line. For all queries the following limits are held: 1 ≤ k ≤ m, |x| ≤ 108. The queries are given in order they need to be answered.
It is guaranteed that the sum of sizes of all sets Sk doesn't exceed 105.
After each first type query print the required sum on a single line.
Please, do not write the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64dspecifier.
5 3 5
5 -5 5 1 -4
2 1 2
4 2 1 4 5
2 2 5
? 2
+ 3 4
? 1
+ 2 1
? 2
-3
4
9
题意:
大小为n的数组a[i], m个集合集合中的元素是数组a的下标,所有集合的元素的总数不大于n,有两种操作:? k 询问a数组下标在k集合中的a[i]的和,
+ k x表示a数组下标在k集合中的a[i]的值加x。
代码:
//普通暴力解法必然超时。把集合分为重集合和轻集合,元素个数大于sqrt(n)的集合是重集合, //否则是轻集合。所有集合的元素总数不大于n,所以重集合个数不超过sqrt(n)个。 //算出每个重集合与其他集合有多少交集t(O(nsqrt(n)))。对于重集合先算出以其中的元素为下标的a[i]的总和sum, //修改的重集合,直接记录该重集合中元素变化了多少tag,修该轻集合时直接修改a[i]的值然后更新 //每个重集合的sum+=两个集合的交集*变化值。 //询问轻集合是直接计算a[i]的和然后加上与他相交的重集合的t*tag。询问重集合时sum+=与他相交的 //重集合的t*tag。除了求交集外其他操作都是O(n),O(sqrt(n))。 #include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=100005; const int maxl=335; int n,m,q; int id[maxn],t[maxl][maxn],vis[maxn]; ll a[maxn],sum[maxn],tag[maxl]; vector<int>s[maxn],big; int main() { scanf("%d%d%d",&n,&m,&q); for(int i=1;i<=n;i++) scanf("%I64d",&a[i]); for(int i=1;i<=m;i++){ int k; scanf("%d",&k); s[i].resize(k); for(int j=0;j<k;j++) scanf("%d",&s[i][j]); if(k>maxl){ id[i]=(int)big.size(); big.push_back(i); for(int j=0;j<k;j++) sum[id[i]]+=a[s[i][j]]; } else id[i]=-1; } memset(vis,0,sizeof(vis)); memset(t,0,sizeof(t)); memset(tag,0,sizeof(tag)); for(int h=0;h<(int)big.size();h++){ int i=big[h]; for(int j=0;j<(int)s[i].size();j++) vis[s[i][j]]=1; for(int k=1;k<=n;k++){ for(int j=0;j<(int)s[k].size();j++) t[h][k]+=vis[s[k][j]]; } for(int j=0;j<(int)s[i].size();j++) vis[s[i][j]]=0; } char ch[3]; int k,x; while(q--){ scanf("%s%d",ch,&k); if(ch[0]=='?'){ ll res=0; if(id[k]<0){ for(int j=0;j<(int)s[k].size();j++) res+=a[s[k][j]]; for(int i=0;i<(int)big.size();i++) res+=tag[i]*t[i][k]; } else{ res=sum[id[k]]; for(int i=0;i<(int)big.size();i++) res+=tag[i]*t[i][k]; } printf("%I64d\n",res); } else{ scanf("%d",&x); if(id[k]<0){ for(int j=0;j<(int)s[k].size();j++) a[s[k][j]]+=x; for(int i=0;i<(int)big.size();i++) sum[i]+=t[i][k]*x; } else tag[id[k]]+=x; } } return 0; }



