Codeforces Round #403 (Div. 2) B 三分 C dfs
The main road in Bytecity is a straight line from south to north. Conveniently, there are coordinates measured in meters from the southernmost building in north direction.
At some points on the road there are n friends, and i-th of them is standing at the point xi meters and can move with any speed no greater than vi meters per second in any of the two directions along the road: south or north.
You are to compute the minimum time needed to gather all the n friends at some point on the road. Note that the point they meet at doesn't need to have integer coordinate.
The first line contains single integer n (2 ≤ n ≤ 60 000) — the number of friends.
The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) — the current coordinates of the friends, in meters.
The third line contains n integers v1, v2, ..., vn (1 ≤ vi ≤ 109) — the maximum speeds of the friends, in meters per second.
Print the minimum time (in seconds) needed for all the n friends to meet at some point on the road.
Your answer will be considered correct, if its absolute or relative error isn't greater than 10 - 6. Formally, let your answer be a, while jury's answer be b. Your answer will be considered correct if 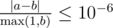 holds.
holds.
3
7 1 3
1 2 1
2.000000000000
4
5 10 3 2
2 3 2 4
1.400000000000
In the first sample, all friends can gather at the point 5 within 2 seconds. In order to achieve this, the first friend should go south all the time at his maximum speed, while the second and the third friends should go north at their maximum speeds.
题意:
从南到北一条啊路上分布着n个人,每人有一个速度,问他们在哪点能够以最短的时间相遇,输出时间精确到1e-6.
代码:
//很显然要相遇的位置一定在最那边的位置和最北边的位置的中间,因为这个位置又是 //用时最少的,所以时间t关于位置x是凹函数,即时间先减后增。这样三分就可以确定 //花费最小时间的位置x然后得出t。但是x不是连续的,如果求得的x不是整数就不能确定t。 //可以二分t,若某一个t对应一大一小两个x,t就继续减小直到最低点。 #include<bits/stdc++.h> using namespace std; int n; double a[60004],b[60004]; int main() { scanf("%d",&n); for(int i=0;i<n;i++) scanf("%lf",&a[i]); for(int i=0;i<n;i++) scanf("%lf",&b[i]); double lef=0.0,rig=1e9,mid; while(rig-lef>=1e-8){ mid=(lef+rig)/2; double lowx=0,higx=1e9; for(int i=0;i<n;i++){ lowx=max(lowx,a[i]-mid*b[i]);//小x higx=min(higx,a[i]+mid*b[i]);//大x } if(lowx<=higx) rig=mid;//向南走的人中最北边的那个和向北走的人中最南边的那个如果有交叉,时间可以再减小 else lef=mid; } printf("%.6lf\n",rig); return 0; }
Andryusha goes through a park each day. The squares and paths between them look boring to Andryusha, so he decided to decorate them.
The park consists of n squares connected with (n - 1) bidirectional paths in such a way that any square is reachable from any other using these paths. Andryusha decided to hang a colored balloon at each of the squares. The baloons' colors are described by positive integers, starting from 1. In order to make the park varicolored, Andryusha wants to choose the colors in a special way. More precisely, he wants to use such colors that if a, b and c are distinct squares that a and b have a direct path between them, and b and c have a direct path between them, then balloon colors on these three squares are distinct.
Andryusha wants to use as little different colors as possible. Help him to choose the colors!
The first line contains single integer n (3 ≤ n ≤ 2·105) — the number of squares in the park.
Each of the next (n - 1) lines contains two integers x and y (1 ≤ x, y ≤ n) — the indices of two squares directly connected by a path.
It is guaranteed that any square is reachable from any other using the paths.
In the first line print single integer k — the minimum number of colors Andryusha has to use.
In the second line print n integers, the i-th of them should be equal to the balloon color on the i-th square. Each of these numbers should be within range from 1 to k.
3
2 3
1 3
3
1 3 2
5
2 3
5 3
4 3
1 3
5
1 3 2 5 4
5
2 1
3 2
4 3
5 4
3
1 2 3 1 2
In the first sample the park consists of three squares: 1 → 3 → 2. Thus, the balloon colors have to be distinct.
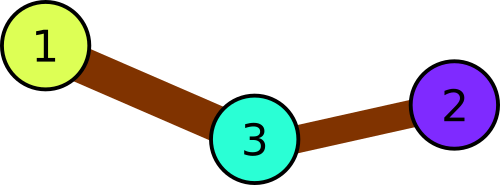 Illustration for the first sample.
Illustration for the first sample.In the second example there are following triples of consequently connected squares:
- 1 → 3 → 2
- 1 → 3 → 4
- 1 → 3 → 5
- 2 → 3 → 4
- 2 → 3 → 5
- 4 → 3 → 5
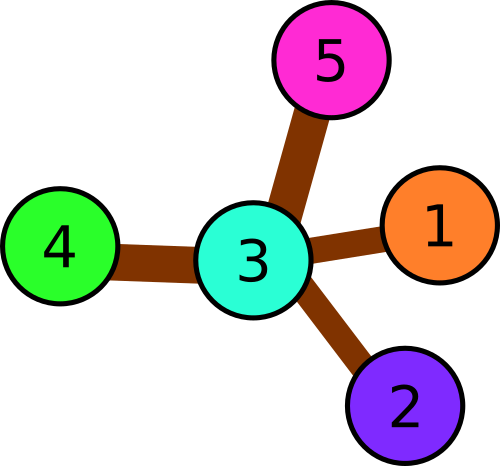 Illustration for the second sample.
Illustration for the second sample.In the third example there are following triples:
- 1 → 2 → 3
- 2 → 3 → 4
- 3 → 4 → 5
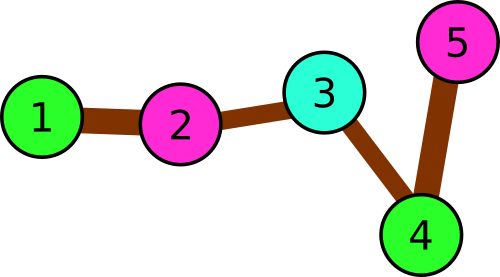 Illustration for the third sample.
Illustration for the third sample.
题意:
n个点,n-1条边,要求相邻的三个点的颜色不能有相同的,需要多少颜色,各是什么颜色。
代码:
//建图之后dfs 重点是染色时没想到怎么处理。 #include<bits/stdc++.h> using namespace std; int n,tol,ans,head[400005],col[200005]; struct node { int v,next; }nodes[400005]; void Add(int x,int y) { nodes[tol].v=y; nodes[tol].next=head[x]; head[x]=tol++; nodes[tol].v=x; nodes[tol].next=head[y]; head[y]=tol++; } void dfs(int x,int f) { int c=1;// for(int i=head[x];i!=-1;i=nodes[i].next){ int y=nodes[i].v; if(y==f) continue; if(c==min(col[x],col[f])) c++; if(c==max(col[x],col[f])) c++; col[y]=c;ans=max(ans,c);c++;//父亲和祖父都没用过c颜色,他兄弟考虑c++颜色。 dfs(y,x); } } int main() { scanf("%d",&n); int a,b;tol=0; memset(head,-1,sizeof(head)); for(int i=0;i<n-1;i++){ scanf("%d%d",&a,&b); Add(a,b); } ans=0; memset(col,0,sizeof(col)); col[1]=1;col[0]=0; dfs(1,0); printf("%d\n",ans); printf("%d",col[1]); for(int i=2;i<=n;i++) printf(" %d",col[i]); printf("\n"); return 0; }



