CF2.C
C. Vladik and fractions
time limit per test
1 secondmemory limit per test
256 megabytesinput
standard inputoutput
standard outputVladik and Chloe decided to determine who of them is better at math. Vladik claimed that for any positive integer n he can represent fraction  as a sum of three distinct positive fractions in form
as a sum of three distinct positive fractions in form 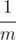 .
.
Help Vladik with that, i.e for a given n find three distinct positive integers x, y and z such that 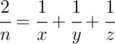 . Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 109.
. Because Chloe can't check Vladik's answer if the numbers are large, he asks you to print numbers not exceeding 109.
If there is no such answer, print -1.
Input
The single line contains single integer n (1 ≤ n ≤ 104).
Output
If the answer exists, print 3 distinct numbers x, y and z (1 ≤ x, y, z ≤ 109, x ≠ y, x ≠ z, y ≠ z). Otherwise print -1.
If there are multiple answers, print any of them.
Examples
Input
3
Output
2 7 42
Input
7
Output
7 8 56
题意:
给出n,问有没有三个数x,y,z,使得1/x+1/y+1/z=2/n;
代码:
1 //直接模拟,枚举比2/n小的分数,从1/(n/2+1)开始到2/n-1/(n/2+1)结束,这样依次得到x,y,z,记住分子分母要约分要 2 //防止超过1e9,判断x,y,z是否符合条件即可。 3 #include<bits\stdc++.h> 4 typedef long long ll; 5 using namespace std; 6 ll gcd(ll x,ll y) 7 { 8 if(y==0) return x; 9 return gcd(y,x%y); 10 } 11 int main() 12 { 13 int n; 14 while(cin>>n) 15 { 16 if(n==1) 17 { 18 cout<<"-1\n"; 19 continue; 20 } 21 ll f1,f2,maxn,minn,f3,f4,x,y,z; 22 if(n&1) 23 { 24 f1=2;f2=n; 25 } 26 else 27 { 28 f1=1;f2=n/2; 29 } 30 minn=(f2+1)/f1; 31 maxn=f2*minn; 32 int flag=0; 33 for(ll i=minn;i<=maxn;i++) 34 { 35 x=i; 36 f4=i*f2; 37 f3=f1*i-f2; 38 ll cnt=gcd(f4,f3); 39 f4/=cnt;f3/=cnt; 40 y=(f4+1)/f3; 41 z=y*f4; 42 ll tem=f3*y-f4; 43 cnt=gcd(z,tem); 44 z/=cnt;tem/=cnt; 45 if(x==y||x==z||z==y||tem!=1||x<=0||y<=0||z<=0||z>1e9||y>1e9||z>1e9) 46 continue; 47 flag=1; 48 break; 49 } 50 if(flag) cout<<x<<" "<<y<<" "<<z<<endl; 51 else cout<<"-1\n"; 52 } 53 return 0; 54 } 55 //本题这样做就麻烦了,其实只有n=1时不能拆成三个分数相加,其余的数都可以拆成1/n,1/(n+1),1/n*(n+1); 56 #include<bits\stdc++.h> 57 using namespace std; 58 int main() 59 { 60 int n; 61 cin>>n; 62 if(n==1) cout<<"-1\n"; 63 else 64 cout<<n<<" "<<n+1<<" "<<n*(n+1)<<endl; 65 return 0; 66 }



