CF-300E-Empire Strikes Back（二分答案 素因子分解+筛法 or 奇葩搞法）

题意：http://codeforces.com/problemset/problem/300/E

问你最小的n，满足 n！整除 ∏ a【i】！

思路：

套路写法是筛出所有素因子，数量统计好

然后二分判断答案里是否有足够的因子数。

二分上界注意一下：(n+m)! /(n!*m!) =C(n+m,m)所以∑a【i】一定足够

 

还有一种写法是：https://blog.csdn.net/dg_programming/article/details/38903083?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

其实可以这样理解，对于一个 i 来说，如果 i 是合数，那么 i 的素因子应该全得再加上 p[ i ] 个，而这里处理的是将 i 的最小素因子加p [ i ]个，然后将 i / minP[ i ]（表示i的最小素因子）加p[ i ]个，i 可以从大到小进行循环，那么如果 i / minP[ i ]还是合数的话，那么会在 i = i / minP[ i ]时处理接下来的 i 的素因子：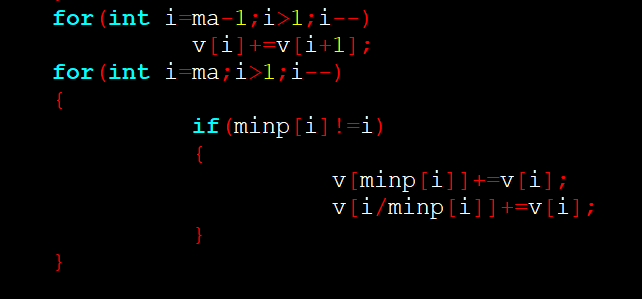

有点背包的意思

  1 #define IOS ios_base::sync_with_stdio(0); cin.tie(0);
  2 #include <cstdio>//sprintf islower isupper
  3 #include <cstdlib>//malloc  exit strcat itoa system("cls")
  4 #include <iostream>//pair
  5 #include <fstream>//freopen("C:\\Users\\13606\\Desktop\\Input.txt","r",stdin);
  6 #include <bitset>
  7 //#include <map>
  8 //#include<unordered_map>
  9 #include <vector>
 10 #include <stack>
 11 #include <set>
 12 #include <string.h>//strstr substr strcat
 13 #include <string>
 14 #include <time.h>// srand(((unsigned)time(NULL))); Seed n=rand()%10 - 0~9;
 15 #include <cmath>
 16 #include <deque>
 17 #include <queue>//priority_queue<int, vector<int>, greater<int> > q;//less
 18 #include <vector>//emplace_back
 19 //#include <math.h>
 20 #include <cassert>
 21 #include <iomanip>
 22 //#include <windows.h>//reverse(a,a+len);// ~ ! ~ ! floor
 23 #include <algorithm>//sort + unique : sz=unique(b+1,b+n+1)-(b+1);+nth_element(first, nth, last, compare)
 24 using namespace std;//next_permutation(a+1,a+1+n);//prev_permutation
 25 //******************
 26 clock_t __START,__END;
 27 double __TOTALTIME;
 28 void _MS(){__START=clock();}
 29 void _ME(){__END=clock();__TOTALTIME=(double)(__END-__START)/CLOCKS_PER_SEC;cout<<"Time: "<<__TOTALTIME<<" s"<<endl;}
 30 //***********************
 31 #define rint register int
 32 #define fo(a,b,c) for(rint a=b;a<=c;++a)
 33 #define fr(a,b,c) for(rint a=b;a>=c;--a)
 34 #define mem(a,b) memset(a,b,sizeof(a))
 35 #define pr printf
 36 #define sc scanf
 37 #define ls rt<<1
 38 #define rs rt<<1|1
 39 typedef pair<int,int> PII;
 40 typedef vector<int> VI;
 41 typedef unsigned long long ull;
 42 typedef long long ll;
 43 typedef double db;
 44 const db E=2.718281828;
 45 const db PI=acos(-1.0);
 46 const ll INF=(1LL<<60);
 47 const int inf=(1<<30);
 48 const db ESP=1e-9;
 49 const int mod=(int)1e9+7;
 50 const int N=(int)1e7+100;
 51 
 52 int prime[N];
 53 ll phi[N];
 54 bool unprime[N];
 55 
 56 ///O(NloglogN)，推荐
 57 void phi_table()
 58 {
 59     int i, j;
 60     for (i = 2; i < N; ++i)
 61         if (!phi[i])
 62             for (j = i; j < N; j += i)
 63             {
 64                 if (!phi[j]) phi[j] = j;
 65                 phi[j] -= phi[j] / i; ///简化后的代码
 66             }
 67 }
 68 
 69 ///O(N)
 70 void linear_phi_table2()
 71 {
 72     int i, j, k = 0;
 73     for (i = 2; i < N; i++)
 74     {
 75         if (!unprime[i]) ///若i为素数，phi(i)=i-1
 76         {
 77             prime[k++] = i;
 78             phi[i] = i - 1;
 79         }
 80         for (j = 0; j < k && prime[j] * i < N; j++)
 81         {
 82             unprime[prime[j] * i] = true;
 83             if (i % prime[j]) ///若i和p互素，则phi(i*p) = phi(i) * phi(p) = phi(i) * (p-1)
 84                 phi[prime[j] * i] = phi[i] * (prime[j] - 1);
 85             else
 86             {
 87                 ///此时有i=kp，则
 88                 ///phi(p*kp) = phi(k*p^2) = p*phi(kp)
 89                 phi[prime[j] * i] = phi[i] * prime[j];
 90                 break;
 91             }
 92         }
 93     }
 94 }
 95 
 96 int a[N],cnt[N];
 97 ll cp[N],check_cp[N];
 98 ll er[100];
 99 ll dp[N];
100 
101 bool check(int r,ll ans)
102 {
103     for(int i=1;i<=r;++i)
104         check_cp[i]=0;
105     for(int i=1;i<=r;++i)
106     {
107         ll temp=prime[i];
108         while(ans/temp)
109         {
110             check_cp[i]+=ans/temp;
111             temp*=prime[i];
112         }
113     }
114     for(int i=1;i<=r;++i)
115         if(cp[i]>check_cp[i])return 0;
116     return 1;
117 }
118 
119 ll get(int r)
120 {
121     ll ans=er[50];
122     for(int i=50;i>=1;--i)
123     {
124         if(check(r,ans-er[i]))
125             ans-=er[i];
126     }
127     return ans;
128 }
129 
130 int main()
131 {
132 /*    int tt=0;
133     for(int i=1;i<=1000;++i)
134     {
135         int t=i;
136         while(t%2)tt++,t/=2;
137     }
138     for(int i=1;i<=1000;++i)
139     {
140         int t=i;
141         while(t%2)tt++,t/=2;
142     }
143     pr("%d\n",tt);
144  */
145     er[1]=1;
146     for(int i=2;i<=100;++i)
147     {
148         er[i]=er[i-1]*2;
149     //    pr("%d: %lld\n",i,er[i]);
150     }
151     linear_phi_table2();
152 //    for(int i=0;i<=100;++i)pr("%d: %d\n",i,prime[i]);
153     int n;
154     sc("%d",&n);
155     int top=0;
156     for(int i=1;i<=n;++i)sc("%d",&a[i]),++cnt[a[i]],top=a[i]>top?a[i]:top;
157     if(top==1)
158     {
159         pr("1\n");
160         return 0;
161     }
162     int r=0;
163     for(int i=1e7;i>=1;--i)
164         cnt[i]+=cnt[i+1];
165     for(int i=1;i<=1e7;++i)
166     {
167         if(prime[i]>top)
168         {
169             r=i-1;
170             break;
171         }
172     }r++;
173 //    for(int i=1;i<=10000000;++i)
174 //        pr("%d: %d\n",i,prime[i]);
175     for(int i=r;i>=1;--i)
176         prime[i]=prime[i-1];
177     for(int i=1;i<=r;++i)
178     {
179         int now=prime[i];
180         ll sum=0;
181         for(int j=1;j*now<=top;++j)
182         {
183             if(j==1)dp[j*now]=1;
184             else
185             {
186                 dp[j*now]=0;
187                 if(j%now==0)dp[j*now]=dp[j]+1;
188                 else dp[j*now]=dp[now];
189             }
190             sum+=dp[j*now]*cnt[j*now];
191         }
192         cp[i]=sum;
193     }
194     pr("%lld\n",get(r));
195     return 0;
196 }
197 
198 /**************************************************************************************/

 

posted @ 2020-03-27 21:51  ZMWLxh  阅读(258)  评论(0)  编辑  收藏  举报