概率DP（放棋子）Domination

题意：https://zoj.pintia.cn/problem-sets/91827364500/problems/91827369874

给你n*m的棋盘，我们定义放满棋盘是：任意一行一列至少有一个棋子。

问你放满棋盘需要棋子的期望数。

思路：

我们先算出用x个棋子放满棋盘的概率，然后求Sigma就可以了

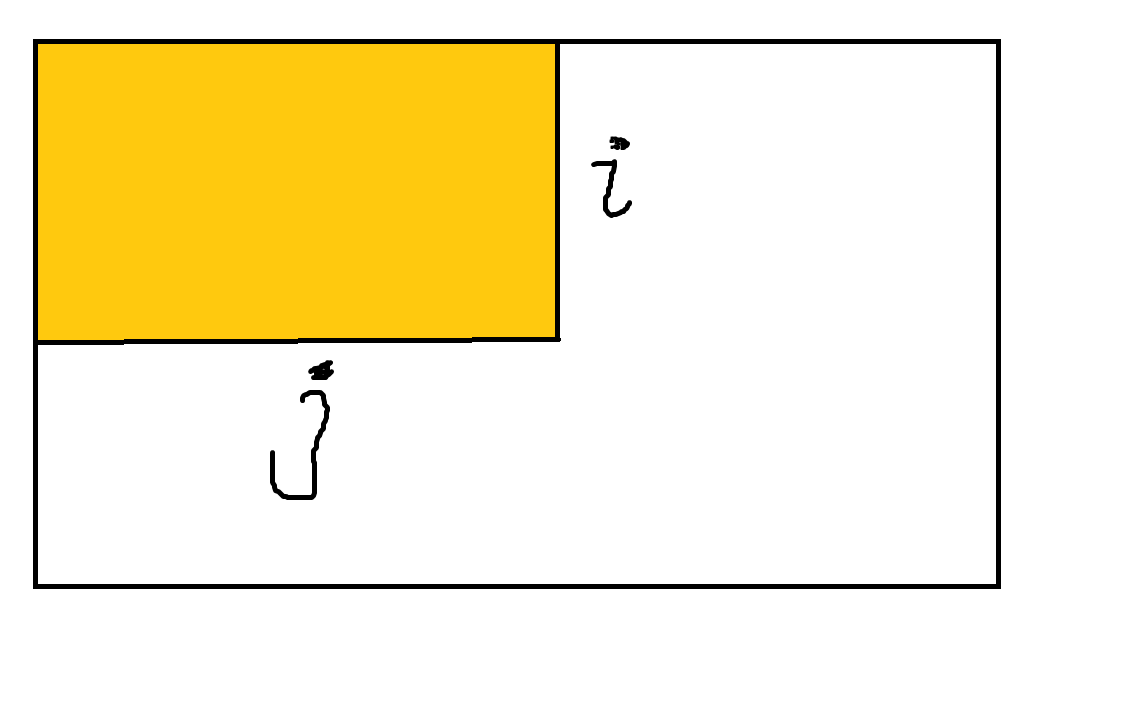
我们可以转换一下放棋子的方式，在任意一个地方放棋子，我们都可以把这个位置尽可能的移到左上角。

dp【k】【i】【j】是放了k个棋子，已经有 i 行 j 列满了的概率；

注意：放最后一个的时候不需要加放在 i，j区域里的概率（既然都放里面了，那就已经放满了）。

#define IOS ios_base::sync_with_stdio(0); cin.tie(0);
#include <cstdio>//sprintf islower isupper
#include <cstdlib>//malloc  exit strcat itoa system("cls")
#include <iostream>//pair
#include <fstream>//freopen("C:\\Users\\13606\\Desktop\\草稿.txt","r",stdin);
#include <bitset>
//#include <map>
//#include<unordered_map>
#include <vector>
#include <stack>
#include <set>
#include <string.h>//strstr substr
#include <string>
#include <time.h>//srand(((unsigned)time(NULL))); Seed n=rand()%10 - 0~9;
#include <cmath>
#include <deque>
#include <queue>//priority_queue<int, vector<int>, greater<int> > q;//less
#include <vector>//emplace_back
//#include <math.h>
//#include <windows.h>//reverse(a,a+len);// ~ ! ~ ! floor
#include <algorithm>//sort + unique : sz=unique(b+1,b+n+1)-(b+1);+nth_element(first, nth, last, compare)
using namespace std;//next_permutation(a+1,a+1+n);//prev_permutation
#define fo(a,b,c) for(register int a=b;a<=c;++a)
#define fr(a,b,c) for(register int a=b;a>=c;--a)
#define mem(a,b) memset(a,b,sizeof(a))
#define pr printf
#define sc scanf
#define ls rt<<1
#define rs rt<<1|1
typedef long long ll;
void swapp(int &a,int &b);
double fabss(double a);
int maxx(int a,int b);
int minn(int a,int b);
int Del_bit_1(int n);
int lowbit(int n);
int abss(int a);
//const long long INF=(1LL<<60);
const double E=2.718281828;
const double PI=acos(-1.0);
const int inf=(1<<30);
const double ESP=1e-9;
const int mod=(int)1e9+7;
const int N=(int)1e6+10;

double dp[55][55][2510];

int main()
{
//    freopen("C:\\Users\\13606\\Desktop\\草稿.txt","r",stdin);
    int T;
    sc("%d",&T);
    while(T--)
    {
        int n,m;
        sc("%d%d",&n,&m);
        dp[0][0][0]=1.0;
        for(int k=1;k<=n*m;++k)
        {
            for(int i=1;i<=n;++i)
            {
                for(int j=1;j<=m;++j)
                {
                     dp[i][j][k]=dp[i-1][j][k-1]*(n+1-i)*j/(n*m+1-k)
                                +dp[i][j-1][k-1]*(m+1-j)*i/(n*m+1-k)
                                 +dp[i-1][j-1][k-1]*(n+1-i)*(m+1-j)/(n*m+1-k);
                    if(i<n||j<m)
                        dp[i][j][k]+=dp[i][j][k-1]*(i*j+1-k)/(n*m+1-k);
                }
            }
        }
        double ans=0;
        for(int i=1;i<=n*m;++i)
            ans+=i*dp[n][m][i];
        pr("%.10lf\n",ans);
    }
    return 0;
}

/**************************************************************************************/

int maxx(int a,int b)
{
    return a>b?a:b;
}

void swapp(int &a,int &b)
{
    a^=b^=a^=b;
}

int lowbit(int n)
{
    return n&(-n);
}

int Del_bit_1(int n)
{
    return n&(n-1);
}

int abss(int a)
{
    return a>0?a:-a;
}

double fabss(double a)
{
    return a>0?a:-a;
}

int minn(int a,int b)
{
    return a<b?a:b;
}