人工智能-实验一策略迭代和值迭代

1.实验问题

在4x4矩阵中添加终点和障碍点，分别有一个或多个，并且满足以下属性：

        终点：value值不变，始终为0，邻接点可到达用大写字母E表示

        障碍点：表示该点在矩阵中“不存在”，邻接点不可到达该点，且该点没有value值跟状态，使用符号‘#’表示

  以任意除以上两种结点之外的所有其它结点为起点，求解起点到终点的最短距离，存在多终点时，以相隔最近的终结点为准。

 

2.实验思路

1）  使用值Policy Iteration和Value Iteration算法分别计算问题产生的最佳策略

2）  设置奖励值r=-1，折扣值disc = 0.57f，使用新旧两个状态矩阵和两个Value矩阵用于迭代过程中保存状态变化和价值变化。

3） MDP模型描述：

      S: 状态集合为{0…15},由4x4的矩阵S存储，状态与状态之间满足马尔可夫属性，因为当前状态可到达的状态最多四个，后继状态只受当前状态影响。

      A：可采取的action集合，使用A={n,e,s,w},北东南西表示

      P：状态转移概率矩阵：不在编程中显式出现，因为迭代时已知继承状态的value值

      R : 因为求解最短距离，agent每行动一步可获的奖励为r=-1

      γ : 折扣因子设置为 0.57，在0~1之间可调，但不能等于0或1，否则会造成无法收敛，无限循环的问题。

4) 值迭代：

       a.初始化每个状态的value值为V(s) = 0;

       b.然后最大化每个状态当前的value值，包括行动奖励和未来奖励，直到value值变化不明显为止

       c.根据以上步骤求得的收敛值矩阵V,对每个状态遍历查找使得总奖励（行动奖励和未来奖励）最大的action，放入策略矩阵S,并打印输出。

 

5）策略迭代：

       a.初始化V矩阵为0，状态矩阵中的每个状态随机选择四个方向之一进行初始化，并且在状态矩阵中添加障碍点’#’和终结点‘E’

       b.根据选择的策略，最优化V矩阵

       c.优化当前策略：如果当前策略并不使得当前状态的value值最大，那么把当前策略替换为最优策略

       d如果对于所有状态，所有策略均未发生改变，那么输出当前的最佳策略，否则继续从b开始循环

 

3.实验结果

 

  1）策略迭代

    不同障碍及不同终节点下的收敛情况，其中 ‘#’表示障碍，‘E’表示终结点

 

 

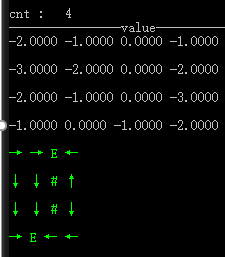
2 ）值迭代

      不同障碍和终结点，折扣值为1.0

        

          

4.实验代码；

   1）策略迭代：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <set>
#include <queue>
#include <windows.h>  
#include <string>

using namespace std;

const int MAX_N = 4;
const float INF = -999999999.0f;
float V[MAX_N][MAX_N];      //值矩阵
float OLDV[MAX_N][MAX_N];    //保存旧的val值
char S[MAX_N][MAX_N];      //状态矩阵，直观存储运动方向
char OLDS[MAX_N][MAX_N];   //旧的状态矩阵
char A[4] = { 'n','e','s','w' };     //Action ,'↑','→','↓','←'
int dx[] = { -1,0,1,0 }, dy[]= { 0,1,0,-1 };  //四向移动
int r = -1;                  //奖励值
float disc = 0.57f;            //折扣值
float en = 0.00000001f;        //sub小于这个数时收敛


//  获取输出流的句柄
HANDLE hOut = GetStdHandle(STD_OUTPUT_HANDLE);

//初始化
void init() {
    for (int i = 0; i < MAX_N; i++)
        for (int j = 0; j < MAX_N; j++) {
            S[i][j] = 'n';                    //初始化为向右走
            OLDS[i][j] = 'n';
        }
    OLDS[0][0] = S[0][0] = '#';                       
      OLDS[3][3] = S[3][3] = 'E';                       //目标点    
      

      OLDS[2][2] = S[2][2] = 'E';      //障碍
      OLDS[2][1] = S[2][1] = '#';
      OLDS[2][3] = S[2][3] = '#';

}

int getIndex(char ch) {
    switch (ch) {
    case 'n':
        return 0;
    case 'e':
        return 1;
    case 's':
        return 2;
    case 'w':
        return 3;
    default:
        return -1;
    }
}

void printVal() {
    puts("----------------value-----------------");
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            printf("%f ", V[i][j]);
        }
        puts("\n");
    }
}
void printState() {
    puts("----------------State-----------------");
    //打印策略
    for (int i = 0; i < MAX_N; i++) {
        printf("        ");
        for (int j = 0; j < MAX_N; j++) {
            switch (S[i][j]) {
            case 'n':
                printf("↑  ");
                break;
            case 'e':
                printf("→  ");
                break;
            case 's':
                printf("↓  ");
                break;
            case 'w':
                printf("←  ");
                break;
            default:
                printf("%c   ", S[i][j]);
                break;
            }
        }
        puts("\n");
    }
}

void PolicyEvaluation(){
    float sub;
    int cnt = 0;
    do{
        sub = 0.0f;
        for (int i = 0; i < MAX_N; i++) {
            for (int j = 0; j < MAX_N; j++) {

                if (S[i][j] != '#' && S[i][j] != 'E') {           //不是障碍物及终点
                    float val = V[i][j];
                    int k = getIndex(S[i][j]);       //根据状态得出移动下标
                    int x = i + dx[k], y = j + dy[k];
                    if (x >= 0 && x < MAX_N && y >= 0 && y < MAX_N && S[x][y] != '#') {
                        V[i][j] = r +  disc * OLDV[x][y];
                    }
                    sub = max(sub, fabs(val - V[i][j]));
                }
            }
       }

        //把新的val值拷贝到旧的数组中
        for (int i = 0; i < MAX_N; i++) {
            for (int j = 0; j < MAX_N; j++) {
                OLDV[i][j] = V[i][j];
            }
        }

        printf("cnt :   %d\n", ++cnt);
        printVal();
            
    } while (sub > en);
}

void PolicyImprovement() {

  while (true) {

    bool stable = true;
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            if (OLDS[i][j] != '#' && OLDS[i][j] != 'E') {
                char oldact = OLDS[i][j];
                int k = 4;
                float ma = INF;
                while (k--) {
                    int x = i + dx[k], y = j + dy[k];
                    if (x >= 0 && x < MAX_N && y >= 0 && y < MAX_N && OLDS[x][y] != '#') {
                        float round = r + disc * OLDV[x][y];
                        if (round - ma > en) {
                            ma = round;    //改变Val值
                            S[i][j] = A[k];    //改变当前状态的最佳策略
                            char ch = A[k];
                        }
                    }
                }

                if (oldact != S[i][j])
                    stable = false;
            }
        }
    }

    //将所有新状态拷贝至旧状态
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            OLDS[i][j] = S[i][j];
        }
    }
        
    if (stable) {
       SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), FOREGROUND_INTENSITY | FOREGROUND_RED);
       printf("\n--------------------------STOP-----------------------\n");

       printVal();
       SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), 0xA); //亮绿
       printState();
       break;
     }
     else {
        PolicyEvaluation();    //继续策略迭代
     }
   }
}


int main() {

    init();
    PolicyEvaluation();
    PolicyImprovement();
    return 0;
}

2）值迭代

   

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <Windows.h>

using namespace std;

const int MAX_N = 4;
const float INF = -999999999.0f;
float V[MAX_N][MAX_N];      //值矩阵
float OLDV[MAX_N][MAX_N];    //保存旧的val值
char S[MAX_N][MAX_N];      //状态矩阵，直观存储运动方向
                           //float P[MAX_N*MAX_N][MAX_N*MAX_N];    //状态转移概率矩阵
char A[4] = { 'n','e','s','w' };     //Action ,'↑','→','↓','←'
int dx[] = { -1,0,1,0 }, dy[] = { 0,1,0,-1 };  //四向移动
int r = -1;                  //奖励值
float disc = 1.0f;            //折扣值
float en = 0.0000001f;        //sub小于这个数时收敛

 //初始化                              
void init() {
    for (int i = 0; i < MAX_N; i++)
        for (int j = 0; j < MAX_N; j++) {
            S[i][j] = 'w';                    //初始化为向右走
        }
    S[0][2] = '#';                       //#障碍
    S[3][1] = 'E';                       //E目标点            
    S[2][2] = '#';
    S[1][2] = 'E';
    S[1][2] = '#';
}


int getIndex(char ch) {
    switch (ch) {
    case 'n':
        return 0;
    case 'e':
        return 1;
    case 's':
        return 2;
    case 'w':
        return 3;
    default:
        return -1;
    }
}

void printVal() {
    puts("----------------value-----------------");
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            printf("%.4f ", V[i][j]);
        }
        puts("\n");
    }
}

void ValueIteration() {
    float sub = 0;
    int cnt = 0;
    do {
        sub = 0;
        for (int i = 0; i < MAX_N; i++) {
            for (int j = 0; j < MAX_N; j++) {
                if (S[i][j] != '#' && S[i][j] != 'E') {           //不是障碍物及终点
                    float val = V[i][j];
                    int k = 4;
                    int ma = INF;
                    while (k--) {
                        int x = i + dx[k], y = j + dy[k];
                        if (x >= 0 && x < MAX_N && y >= 0 && y < MAX_N && S[x][y] != '#') {
                            float round = r + disc * OLDV[x][y];
                            if (ma < round) {
                                 ma = round;    //改变Val值
                            }
                        }
                    }
                    if (ma != INF)
                        V[i][j] = ma;                        //V[i][j]取得周围环境的最大值

                    sub = max(sub, fabs(val - V[i][j]));
                }
            }
        }

        //把新的val值拷贝到旧的数组中
        for (int i = 0; i < MAX_N; i++) {
            for (int j = 0; j < MAX_N; j++) {
                OLDV[i][j] = V[i][j];
            }
        }
        printf("cnt :   %d\n", ++cnt);
        printVal();

    } while (sub >= en);


    //更新最佳策略
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            if (S[i][j] != '#' && S[i][j] != 'E') {           //不是障碍物及终点
                int k = 4;
                int ma = INF;
                while (k--) {
                    int x = i + dx[k], y = j + dy[k];
                    if (x >= 0 && x < MAX_N && y >= 0 && y < MAX_N && S[x][y] != '#') {
                        float round = r + disc * OLDV[x][y];
                        if (ma < round) {
                            ma = round;    //改变Val值
                            S[i][j] = A[k];
                        }
                    }
                }
            }
        }
    }

    SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), 0xA); //亮绿
    //打印策略
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            char ch;
            switch (S[i][j]) {
              case 'n':
                  printf("↑ ");
                  break;
              case 'e':
                  printf("→ ");
                  break;
              case 's':
                  printf("↓ ");
                  break;
              case 'w':
                  printf("← ");
                  break;
              default:
                  printf("%c ", S[i][j]);
                  break;
            }
        }
        puts("\n");
    }

}


int main() {

    init();
    ValueIteration();
    return 0;
}