Atcoder | AT2665 【Moderate Differences】

又是一道思路特别清奇的题qwq...(瞪了一上午才发现O(1)的结论...差点还想用O(n)解决)
问题可以转化为是否能够由\(f_{1}=a\)通过\(\pm x \in[c,d]\)得到\(f_{n}=b\),于是考虑用数学方法解决
证明比较简单...就是...能想到这一点就很毒瘤了qwq...让我来随手拿一个样例举例qwq

输入样例2：4 7 6 4 5
输出样例2：NO

丝毫不想画图...太乱惹qwq
为了能看的更明白我还是画吧qwq(感谢GeoGebra)
注：横坐标表示框内数值,纵坐标表示编号(宽屏没办法qwq...看不清就保存图片放大...还是能看清楚一点的...实在不行下面会放坐标)
下面的图片可以在新的标签页中打开放大...经测试清晰度可以接受

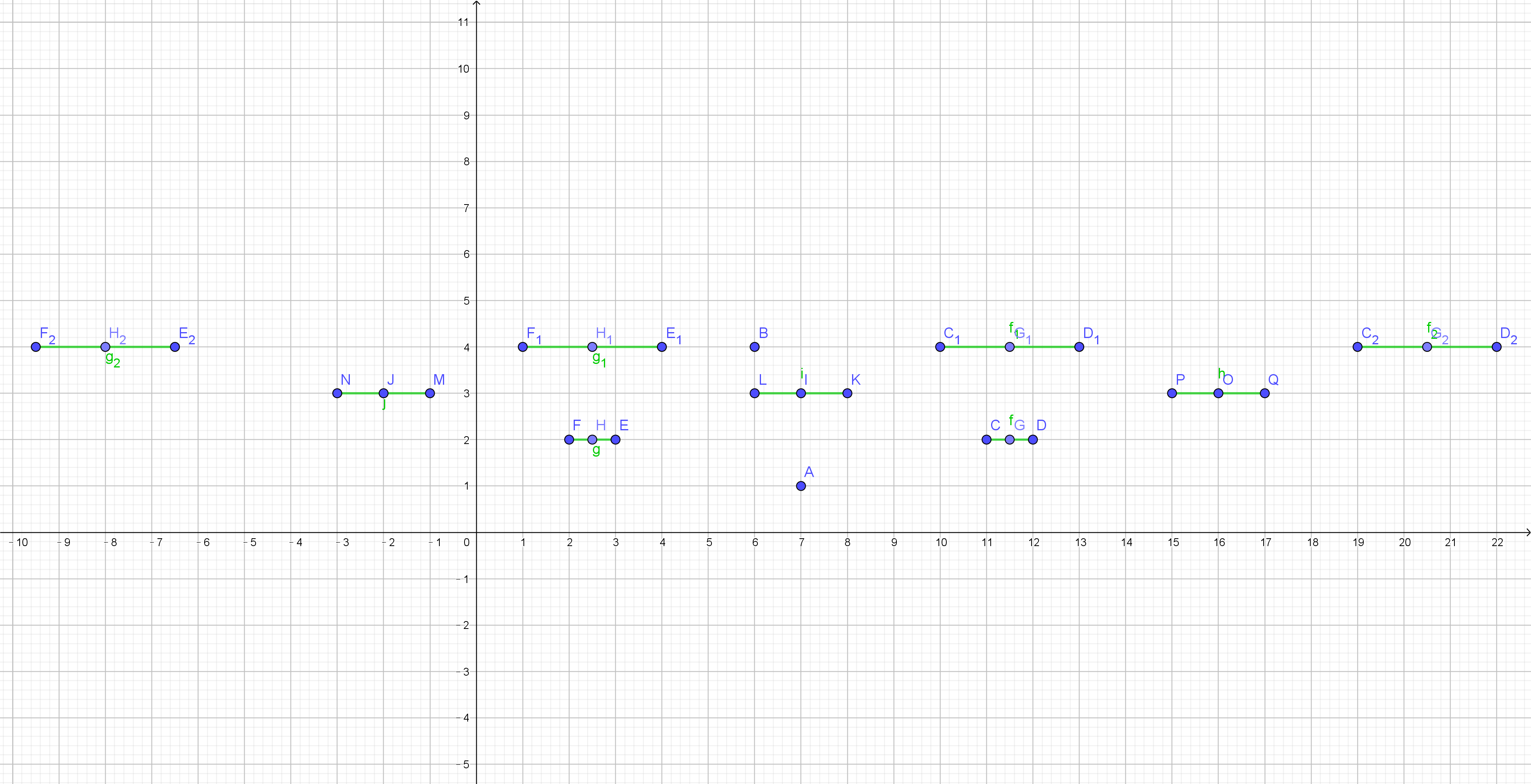
做出上图后发现,绿色线段对应位置是可以到达的,此时问题转化为点\(B\)是否在某一条绿色线段(含端点)上
取所有线段中点后发现,在纵坐标为奇数时,所有线段中点到点\(A\)的横坐标距离为\(2k \times \frac{c+d}{2}(k \in N)\),在纵坐标为奇数时,所有线段中点到A的横坐标距离为\((2k+1) \times \frac{c+d}{2}(k \in N)\),位于\(y=k\)上的最远的线段中点到点\(A\)的横坐标距离为\((k-1) \times \frac{c+d}{2}\),且长度为\((k-1) \times (d-c)\),也即点\(B\)与点\(A\)的横坐标距离\(\leq (n-1) \times \frac{c+d}{2}\)且与位于\(y=n\)上某条线段的中点距离\(\leq \frac{(n-1) \times (d-c)}{2}\)时由\(A\)可以到达\(B\),所以只需要按照\(n\)的奇偶性分类\(O(1)\)计算结果即可.
全都是数学推导...感性理解一下就好
下面放代码$\downarrow \downarrow \downarrow $

#include<cstdio>//AT2665
#include<iostream>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<cstdlib>

using namespace std;

int n,a,b,c,d,delta,whole;

double nxt,half=0.5,maxhalf,lft;

int main(){
    scanf("%d%d%d%d%d",&n,&a,&b,&c,&d);
    nxt+=c+d;
    nxt/=2;
    half=nxt-c;
    maxhalf=half*(n-1);
    delta=abs(a-b);
    if(delta>(n-1)*nxt+maxhalf){//超过最远距离
        printf("NO\n");
        return 0;
    }
    whole=(int)(delta/nxt);
    lft=delta-nxt*whole;
    if(n&1){//n%2==1
        if(whole&1){
            lft=nxt-lft;
            if(lft<=maxhalf){
                printf("YES\n");
                return 0;
            }
            else{
                printf("NO\n");
                return 0;
            }
        }
        else{
            if(lft<=maxhalf){
                printf("YES\n");
                return 0;
            }
            else{
                printf("NO\n");
                return 0;
            }
        }
    }
    else{//n%2==0
        if(whole&1){
            if(lft<=maxhalf){
                printf("YES\n");
                return 0;
            }
            else{
                printf("NO\n");
                return 0;
            }
        }
        else{
            lft=nxt-lft;
            if(lft<=maxhalf){
                printf("YES\n");
                return 0;
            }
            else{
                printf("NO\n");
                return 0;
            }
        }
    }
    return 0;
}