[模板]KMP算法

昨天晚上一直在调KMP(模板传送门)，因为先学了hash[关于hash的内容会在随后进行更(gu)新(gu)]于是想从1开始读。。。结果写出来之后一直死循环，最后我还是改回从0读入字符串了。
[预先定义被匹配文本串为s1，长度为m；匹配模式串为s2，长度为n]
KMP算法在字符串匹配算法中时间复杂度比较优，可以做到在O(m+n)的时间内匹配，相对于无脑暴力匹配的O(m*n)复杂度而言要优很多。
KMP算法的思路比较简单，即在匹配前对字符串进行预处理，用空间换时间，通过处理next数组来实现在部分失配后的快速再匹配(从前缀中与已匹配部分的后一个字符开始继续匹配)，从而避免不必要的重复检验、节省时间。
预处理next数组在KMP算法中发挥着非常重要的作用，也是KMP算法中比较难理解的部分，下面用一张图来解释预处理的原理和方式：

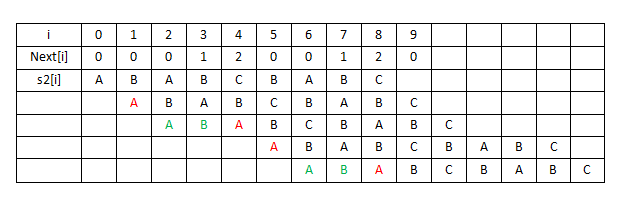
对于需要预处理的模式串s2(以“ABABCBABC”为例)，从s2[1]开始(k=next[1]=0)，发现s2[1]!=s2[0]失配(红色标注)，执行操作A3，令next[1+1]=next[2]=0；对于s2[2] (k=next[2]=0)，发现s2[2]s2[0]匹配(绿色标注)，执行操作A2使next[3]=0+1=1；对于s2[3] (k=next[3]=1)，s2[3]s2[1]，执行操作A2使next[3+1]=1+1=2；s2[4] (k=next[4]=2)!=s2[2]，执行操作A1(k=next[k]=next[2]=0)，s2[4]!=s2[0]，执行操作A3，next[4+1]=0；s2[5] (k=next[5]=0)!=s2[0]，执行操作A3，next[5+1]=0；s2[6] (k=next[6]=0)s2[0]，执行操作A2，next[6+1]=0+1=1；s2[7] (k=next[7]=1)s2[1]，执行操作A2，next[7+1]=1+1=2；s2[8] (k=next[8]=2)!=s2[2]，执行操作A1，(k=next[k]=next[2]=0)，s2[8]!=s2[0]，执行操作A3，next[8+1]=0。
至此next[]已完成预处理，next[]={0,0,0,1,2,0,0,1,2,0}(时间复杂度O(n))。
在完成了预处理next数组的操作后便需要做最后的匹配工作，同样配图来解释：

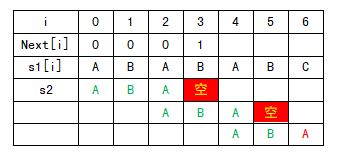
对于s1和s2的匹配(以"ABABABC"和“ABA”为例，以相同方式处理得next[]={0,0,0,1})，从s1[0]开始(k=0，cnt=0)，s2[0]s1[0]，执行操作B2，k=0+1=1；s1[1] (k=1，cnt=0)s2[1]，执行操作B2，k=1+1=2；s1[2] (k=2，cnt=0)s2[2]，执行操作B2，k=2+1=3，此时klen2=3，执行操作B3，cnt=0+1=1，ans[1]=2-3+2=1；s1[3] (k=3，cnt=1)!=s2[3] (s2[3]为空)，执行操作B1，k=next[k]=next[3]=1，s1[3]s2[1]，执行操作B2，k=1+1=2,；s1[4] (k=2，cnt=1)s2[2]，执行操作B2，k=2+1=3len2，执行操作B3，cnt=1+1=2，ans[2]=4-3+2=3；s1[5] (k=3，cnt=2)!=s2[3] (s2[3]为空)，执行操作B1，k=next[k]=next[3]=1，s1[5]s2[1]，执行操作B2，k=1+1=2；s1[6] (k=2，cnt=2)!=s2[2]，执行操作B1，k=next[k]=next[2]=0，s1[6]!=s2[0]，不再执行操作，循环结束。
至此得到ans[]={0,1,3}，cnt=2，匹配完成(时间复杂度O(m))。
以上就是本蒟蒻对KMP算法的个人理解，如果看了以上的叙述仍然不能理解KMP算法的实现可以考虑结合代码进行手动的模拟，具体实现代码如下：

#include<cstdio>//P3375
#include<iostream>
#include<algorithm>
#include<set>
#include<vector>
#include<queue>
#include<string>
#include<cstring>
#include<cstdlib>
#include<cmath>

const int L=1000010;

using namespace std;

char s1[L],s2[L];

int nxt[L],ans[L],cnt;

void getnext(){
    int len=strlen(s2),k;
    for(int i=1;i<len;i++){//如果从i=0开始会导致k=0->next[k]=0死循环
        k=nxt[i];
        while(k&&s2[i]!=s2[k]){//失配则回到前面能继续匹配的子串继续匹配(操作A1)
            k=nxt[k];
        }
        if(s2[k]==s2[i]){//可以匹配时改变next[i+1]值(操作A2)
            nxt[i+1]=k+1;
        }
        else{//(操作A3)
            nxt[i+1]=0;//无法继续匹配next改为0
        }
    }
}

void KMP(){
    int len1=strlen(s1),len2=strlen(s2);
    getnext();
    int k=0;
    for(int i=0;i<len1;i++){
        while(k&&s2[k]!=s1[i]){//部分匹配后失配前跳(操作B1)
            k=nxt[k];
        }
        if(s2[k]==s1[i]){//完成匹配对k后移准备检验下一位匹配(操作B2)
            k++;
        }
        if(k==len2){//完成完全匹配记录匹配位置(操作B3)
            ans[++cnt]=i-len2+2;
        }
    }
}

int main(){
    scanf("%s",s1);
    scanf("%s",s2);
    KMP();
    int len2=strlen(s2);
    for(int i=1;i<=cnt;i++){
        printf("%d\n",ans[i]);
    }
    for(int i=1;i<=len2;i++){
        printf("%d ",nxt[i]);
    }
    return 0;
}