莫比乌斯反演---基础
前置芝士:
1.数论函数
:指定义域为正整数、陪域为复数的函数,每个算术函数都可视为复数的序列。
---来自百度百科
2.积性函数:
若f(x)为一个数论函数,且对于每一个互质的a,b满足
\[f(a*b)=f(a)*f(b)
\]
则f(x)为积性函数.
--完全积性函数:若f(x)为一个数论函数,且对于每一对a,b满足
\[f(a*b)=f(a)*f(b)
\]
则f(x)为完全积性函数.
例:积性函数有:
\[\\\sigma_{k}(n)(表示n的所有约数的k次幂的和)
\\
\varphi(n)也为不超过n且与n互质的数的个数.
\\
\mu(n) = \begin{cases}
1&n=1 \\
(-1)^k&n为k个不同质数的积\\
0&else
\end{cases}
\]
完全积性函数有:
\[幂函数 n^k\\
单位函数\epsilon(n)=\begin{cases}
1&n=1\\
0&n>1
\end{cases}
\]
把积性函数与狄利克雷卷积(下面要学)联系起来,可以得到
若f,g为积性函数,则f*g也为积性函数.
\[(f*g)(a\times b)=\sum\limits_{d|ab}f(d)g(\frac{ab}{d})\\
令d=d_1\times d_2\\
=\sum\limits_{d_1d_2|ab}f(d_1d_2)g(\frac{ab}{d_1d_2})\\
=\sum\limits_{d_1|a}f(d_1)g(\frac{a}{d_1})\times \sum\limits_{d_2|d}f(d_2)g(\frac{b}{d_2})\\
=(f*g)(a)\times (f*g)(b)
\]
线性筛(实际上是利用线性筛求积性函数的值)
唯一分解定理:任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积
那么有
\[\mathbf{f}(n)=\prod\limits_{i=1}^t\mathbf{f}(p_i^{k_i})
\]
于是我们就有另一种方法表示积性函数,即给出它在素数幂处的取值
当我们在线性筛的时候可以求出每个数的最小质因数\(p_1\),它的次数\(k_1\),那么
\[\mathbf{f}(n)=\mathbf{f}(p_1^{k_1})\mathbf{f}(\frac{n}{p_1^{k_1}})
\]
由上面的结论可知:
\[\sigma_0(n)=\prod\limits_{i=1}^t(k_i+1)\\
\phi(n)=\prod\limits_{i=1}^tp_i^{k_i-1}(p_i-1)=n\prod\limits_{i=1}^t(1-\frac{1}{p_i})
\]
(下面的那个是不是有点熟悉?就是课本上欧拉函数的求法)
3.函数之间的加法和数乘
\[(f+g)(n)=f(n)+g(n)
\\加法\\(x\times f)(n)=x\times f(n),x\epsilon C\\
(c为常数) 数乘
\]
4.狄利克雷卷积(Dirichlet)
Dirichlet是个人,而且是一个很有名的人,今天我们不讲这个人,我们讲讲他的狄利克雷卷积
狄利克雷乘积(Dirichlet product)亦称狄利克雷卷积、卷积,是数论函数的重要运算之一。设f(n)、g(n)是两个数论函数,它们的Dirichlet(狄利克雷)乘积也是一个数论函数,简记为h(n)=f(n)*g(n)。---来自百度百科
\[(f*g)=\sum\limits_{ij=n}f(i)g(j)\\或\\(f*g)=\sum\limits_{d|n}f(d)f(\frac{n}{d})
\]
运算性质:满足交换律,结合律,分配律;
交换律 即
\[(f*g)=(f*g)\\
\]
\[--------------\\
证明:\\(f*g)(n)=\sum\limits_{ij=n}f(i)g(j)=\sum\limits_{ji=n}f(j)g(i)=(g*f)(n)
\]
结合律:
\[(f*g)*h=f*(g*h)
\]
\[证明:\\ [((f*g)*h)](n)=\sum\limits_{pq=n}[\sum\limits_{ij=p}f(i)g(j)]h(q)\\
=\sum\limits_{i|n}f(i)(\sum\limits_{jq=\frac{n}{i}}g(j)h(q))\\
=\sum\limits_{i|n}f(i)(g*h)(\frac{n}{i})\\
=(f*(g*h))(n)
\]
分配律:
\[f*(g+h)=f*g+f*h
\]
\[证明:\\
f*(g+h)=[f*(g+h)](n)\\
=\sum\limits_{d|n}f(d)\times[g(\frac{n}{d})+h(\frac{n}{d})]\\
=\sum\limits_{d|n}[f(d)g(\frac{n}{d})+f(d)h(\frac{n}{d})]\\
=f*g+f*h
\]
单位元
在狄利克雷卷积中存在一种像单位矩阵一样的"数",任何一个函数*这个"数"都会是其本身,我们把这个"数"叫做单位元,即前文所提到的单位函数
\[\epsilon(n)=\begin{cases}1&n=1\\
0&n>1\\
\end{cases}
\]
则有
\[(f*\epsilon)(n)=\sum\limits_{d|n,d\neq n}f(d)\epsilon(\frac{n}{d})+f(n)\epsilon(1)\\
=\sum\limits_{d|n,d\neq n}f(d)\times0+1\\]
=f(n)
\]
所以任何一个数论函数与单位元的卷积为数论函数本身(后文有重要运用)
逆元
其实逆元的概念和倒数差不多,即:
方程 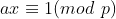 的解称为
的解称为  关于模
关于模 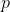 的逆,当
的逆,当 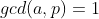 (即
(即  ,
,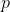 互质)时,方程有唯一解,否则无解。
互质)时,方程有唯一解,否则无解。
那么逆元可以用来干什么呢,比如说对于 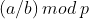 ,并没有
,并没有 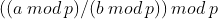 ,但是直接除又会爆精度,这时我们就可以用到逆元,假设用
,但是直接除又会爆精度,这时我们就可以用到逆元,假设用 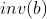 代表
代表 
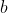 的逆元,那么
的逆元,那么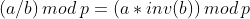 。 ____引用自forever_dreams的博客
。 ____引用自forever_dreams的博客
上面的是数的逆元,狄利克雷卷积也有逆元:
定义:
\[对每个\mathbf{f}(1) \neq 0的函数\mathbf f ,都存在一个函数\mathbf{g}使得\mathbf{f}*\mathbf{g}=\epsilon
\]
则如何求一个函数的逆?
定义
\[\mathbf{g}(n)=\frac{1}{\mathbf{f}(1)}\left([n=1]-\sum\limits_{ij=n,i\neq 1}\mathbf{f}(i)\mathbf{g}(j)\right)
\]
则
\[\mathbf{f}*\mathbf{g}(n)\\
=\sum\limits_{ij=n}\mathbf{f}(i)\mathbf{g}(j)\\
=\mathbf{f}(1)\mathbf{g}(n)+\sum\limits_{ij=n,i\neq 1}\mathbf{f}(i)\mathbf{g}(j)\\=[n=1]=\epsilon(i)
\]
把积性函数和逆元联系起来得到 积性函数的逆元一定也是积性函数.
留与读者自证之/笑哭.(注,积性函数一定满足 f ( 1 ) = 1 )
莫比乌斯反演
\[我们定义1的逆是 \mu.\\
这样的话,如果g=f*1,就有f=f*1*\mu=g*\mu,\\
换句话说,如果 \mathbf g(n)=\sum_{d\mid n}\mathbf f(d) \\就有 \mathbf f(n)=\sum_{d\mid n}\mu\left(\frac nd\right)\mathbf g(d)
\]
\[引理
\\\mu*1=\epsilon\\
即 \sum\limits_{d|n}\mu(d)=\epsilon(n)\\其中的"1"是一个返回值为1的常数函数
\]
证明:
\[设n有k个不同的质因子
\\n=p_1\times p_2\times ...\times p_k\\
记一个函数q(s)为序列\mathbf{s}中所有元素的乘积\\
\mathbf{s}=\{{x_1,x_2...x_k}\};s序列长度为K
\\令一个\mathbf{f}(s)的约数d=\mathbf{f}(j)
\\j\subseteq s,\ \ \ \ j序列长度为J\\
\therefore \sum\limits_{d|n}\mu(d)=\sum\limits_{\mathbf{J}=0}^k\mu(f(j))\times (从K中取J个值(组合数))\\
令i=J,则原式=\sum\limits_{i=0}^k\mu(d)^i(k中取i的组合)\\
根据二项式定理,奇数项与偶数项和为0.
所以\sum\limits_{d|n}\mu(n) = \begin{cases}
1&n=1 \\
0&n>1\\
\end{cases}=\epsilon(n)
\]
求解μ
\[如何求\mu\ ?由于1是积性的,所以1的逆\mu也是积性的,则
\]
\[\mu(p^k)\begin{cases}1,&k=0\\-1,&k=1\\0,&k>1\end{cases}
\]
\[\mu(x)=\begin{cases}
1,&x=1\\
(-1)^n, &x=\prod\limits_{i=1}^np_i\\
0,&其余情况
\end{cases}
\]
\[求\mu的函数
\]
void get_mu(int n)
{
mu[1] = 1;
for(int i = 2;i <= n; i++)
{
if(!vis[i])
{
pri[++cnt] = i;
mu[i] = -1;
}
for(int j = 1; j <= cnt && pri[j] * i <= n; j++)
{
vis[pri[j] * i] = 1;
if(i % pri[j] == 0) break;
else mu[i * pri[j]] = -mu[i];
}
}
}
这样就证明了上述结论。
当然还有另一个方向的莫比乌斯反演(这个大概更常用)
\[\mathbf{g}(n)=\sum\limits_{n|d}\mathbf{f}(d)\iff \mathbf{f}(n)=\sum\limits_{n|d}\mu(\frac{d}{n})\mathbf{g}(d)
\]
\[对此只需要定义 (\mathbf f\oplus\mathbf g)(x)=\sum_{x\mid y}\mathbf f(y/x)\mathbf g(y)=\sum\limits_{x|Y}f(y/x)g(y) ,并容易证明 (\mathbf f\ast\mathbf g)\oplus\mathbf h=\mathbf f\oplus(\mathbf g\oplus\mathbf h)。\\于是
\mathbf f=(\mu\ast\mathbf1)\oplus\mathbf f=\mu\oplus(\mathbf1\oplus\mathbf f)=\mu\oplus\mathbf g
\]
莫比乌斯反演是一个很重要的数论知识,在做数论题的时候很有帮助,为了提高对于莫比乌斯反演的理解和掌握
建议去看看以下几道题
YY的GCD
约数个数和
如果你看完了一遍,对于知识点还是没有理解的话,建议重新看一遍,或者去以下的博客那里看一看,
本人就是从那里学习的
铃悬的小知识
的解称为
关于模
的逆,当
(即
,
互质)时,方程有唯一解,否则无解。
,并没有
,但是直接除又会爆精度,这时我们就可以用到逆元,假设用
代表
的逆元,那么
。 ____引用自forever_dreams的博客


