Codeforces Round #344 (Div. 2) E. Product Sum 三分

E. Product Sum

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Blake is the boss of Kris, however, this doesn't spoil their friendship. They often gather at the bar to talk about intriguing problems about maximising some values. This time the problem is really special.

You are given an array a of length n. The characteristic of this array is the value 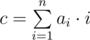 — the sum of the products of the values aiby i. One may perform the following operation exactly once: pick some element of the array and move to any position. In particular, it's allowed to move the element to the beginning or to the end of the array. Also, it's allowed to put it back to the initial position. The goal is to get the array with the maximum possible value of characteristic.

Input

The first line of the input contains a single integer n (2 ≤ n ≤ 200 000) — the size of the array a.

The second line contains n integers ai (1 ≤ i ≤ n, |ai| ≤ 1 000 000) — the elements of the array a.

Output

Print a single integer — the maximum possible value of characteristic of a that can be obtained by performing no more than one move.

Examples

input

4
4 3 2 5

output

39

input

5
1 1 2 7 1

output

49

input

3
1 1 2

output

9

Note

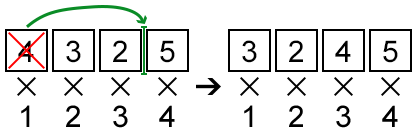
In the first sample, one may pick the first element and place it before the third (before 5). Thus, the answer will be3·1 + 2·2 + 4·3 + 5·4 = 39.

In the second sample, one may pick the fifth element of the array and place it before the third. The answer will be1·1 + 1·2 + 1·3 + 2·4 + 7·5 = 49.

在整数上的三分果然要比在小数上的三分需要注意的事要多一点。。。

首先是要将res初值赋为端点值max(f(l),f(r))，因为整数三分的过程是取不到端点值的，这样就需要在一开始特判l>r时直接返回-INF或INF。看来还是有必要弄个三分的模板的，虽然简单。。

#include<bits/stdc++.h>
#define REP(i,a,b) for(int i=a;i<=b;i++)
#define MS0(a) memset(a,0,sizeof(a))

using namespace std;

typedef long long ll;
const int maxn=1000100;
const ll INF=1e18+10;

int n;
ll a[maxn],s[maxn],is[maxn];

ll getS(int l,int r)
{
    return l>r?0:s[r]-s[l-1];
}

ll getIs(int l,int r)
{
    return l>r?0:is[r]-is[l-1];
}

ll f(int x,int y,int tag)
{
    if(tag==0) return getIs(1,x-1)+getIs(x+1,n)+y*a[x]-getS(x+1,y);
    return getIs(1,x-1)+getIs(x+1,n)+y*a[x]+getS(y,x-1);
}

ll bin3(int l,int r,int x,int tag)
{
    if(l>r) return -INF;
    ll res=max(f(x,l,tag),f(x,r,tag));
    while(l<=r){
        int m=(l+r)>>1,mm=(m+r)>>1;
        ll fm=f(x,m,tag),fmm=f(x,mm,tag);
        if(fm<=fmm) l=m+1;
        else r=mm-1;
        res=max(res,max(fm,fmm));
    }
    return res;
}

ll solve()
{
    ll res=is[n];
    REP(x,1,n){
        ll A=bin3(x+1,n,x,0);
        ll B=bin3(1,x-1,x,1);
        res=max(res,max(A,B));
    }
    return res;
}

int main()
{
    freopen("in.txt","r",stdin);
    while(cin>>n){
        s[0]=is[0]=0;
        REP(i,1,n) scanf("%I64d",&a[i]),s[i]=s[i-1]+a[i],is[i]=is[i-1]+a[i]*i;
        printf("%I64d\n",solve());
    }
    return 0;
}