早晨训练赛第一场 C题

早晨训练赛第一场 C题

C - Searching for Graph

Time Limit:1000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status Practice CodeForces 402C

Description

Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:

• the graph contains exactly 2n + p edges;
• the graph doesn't contain self-loops and multiple edges;
• for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.

A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.

Your task is to find a p-interesting graph consisting of n vertices.

Input

The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 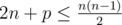) — the number of vertices in the graph and the interest value for the appropriate test.

It is guaranteed that the required graph exists.

Output

For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers a_i, b_i (1 ≤ a_i, b_i ≤ n; a_i ≠ b_i) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.

Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.

Sample Input

Input

1
6 0

Output

1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6
题意：定义一个n个顶点的p-interesting图为：边数为2*n+p，且任意一个k个顶点的子图的边数小于等于2*k+p。（图中没有自回路和多重边）
思路：看样例都可以看出规律吧。。。按样例的方式建图，最坏情况子图顶点为1,2,...k时边数最多，然而显然此时的边数还是不超过2*k+p，因为该子图和原图是同种形式的。因此只要按字典序从小到大遍历边，直到边数超过2*n+p为止。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>

using namespace std;

const int maxn=1000100;
const int INF=(1<<29);

int T;
int n,p;

int main()
{
    cin>>T;
    while(T--){
        cin>>n>>p;
        int cnt=0;
        bool flag=0;
        for(int i=1;i<n;i++){
            for(int j=i+1;j<=n;j++){
                cout<<i<<" "<<j<<endl;
                cnt++;
                if(cnt==2*n+p) flag=1;
                if(flag) break;
            }
            if(flag) break;
        }
    }
    return 0;
}