最大流EK算法/DINIC算法学习

　　之前一直觉得很难，没学过网络流，毕竟是基础知识现在重新来看。

　　定义一下网络流问题，就是在一幅有向图中，每条边有两个属性，一个是cap表示容量，一个是flow

表示流过的流量。我们要求解的问题就是从S点到T点最多可以跑多少流量。用比较学术的话说，就是 一个有向图 G=(V，E)；有两个特别的点：源点s、汇点t；图中每条边(u,v)∈E，有一个非负值的容量C(u,v)，流量F(u,v)。

　　定义一下"残流网络":即当前边还可以流过的流量，也就是cap-flow。

　　　

　　其中，在最大流的问题中，我们要满足三个条件：

1：容量限制：f（u，v）<c（u，v），即每条边流过的流量不能超过容量上限。

2：斜对称性：（f（u，v）=-f（v,u））在后面的运用中，我们叫做一旦有物品从u运到v，那么则肯定有一个可退流从v运到u(这里不懂得稍后解释正确性)。

3：流量平衡：简单来说就是除了源点和汇点，没有其他点可以保存货物。显然f（s，u）==f（v，t）。也就是说非ST节点不累计流量，流进的等于流出的流量。

　　　　最大流问题，就是使得f(s,u)=f(v,t)达到最大。

 

　　现在讨论如何解决这个问题，有一个很容易想到的贪心思路是:我们暴力的从S点到T点找可行路，一旦找到一条路，总流量就加上这条路径上的MIN{cap-flow} ,因为最小的限制最大的。

比如下图: <c,f>表示当前弧的容量及流过的流量。

　　

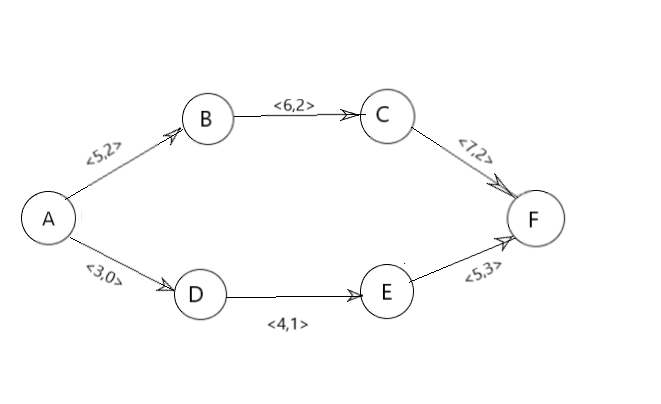
　　如果我们要求A->F的最大流的话，先找到第一条可行路(A->B->C->F),这条路上的最大允许通过的流量是5-2=3，执行之后，A->B这条路上就满流了，也就是不能从A->B在通过流量了。第二次找的时候显然只能找到(A->D->E->F)这条路，最大通过流量是5-3=2 ，第三次就找不到路了。答案就是2+3=5;

　　这样看来这种方法貌似可行，可惜的是有一点没考虑到，如果我们第一次找到的路影响到后面的流的行走导致最优解发生变化怎么办。程序没有反悔的机会，比如下图:

　　

 

 

 

http://acm.hdu.edu.cn/showproblem.php?pid=1532

 

 

Drainage Ditches

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 20435    Accepted Submission(s): 9804

Problem Description

Every time it rains on Farmer John's fields, a pond forms over Bessie's favorite clover patch. This means that the clover is covered by water for awhile and takes quite a long time to regrow. Thus, Farmer John has built a set of drainage ditches so that Bessie's clover patch is never covered in water. Instead, the water is drained to a nearby stream. Being an ace engineer, Farmer John has also installed regulators at the beginning of each ditch, so he can control at what rate water flows into that ditch.
Farmer John knows not only how many gallons of water each ditch can transport per minute but also the exact layout of the ditches, which feed out of the pond and into each other and stream in a potentially complex network.
Given all this information, determine the maximum rate at which water can be transported out of the pond and into the stream. For any given ditch, water flows in only one direction, but there might be a way that water can flow in a circle.

 

 

Input

The input includes several cases. For each case, the first line contains two space-separated integers, N (0 <= N <= 200) and M (2 <= M <= 200). N is the number of ditches that Farmer John has dug. M is the number of intersections points for those ditches. Intersection 1 is the pond. Intersection point M is the stream. Each of the following N lines contains three integers, Si, Ei, and Ci. Si and Ei (1 <= Si, Ei <= M) designate the intersections between which this ditch flows. Water will flow through this ditch from Si to Ei. Ci (0 <= Ci <= 10,000,000) is the maximum rate at which water will flow through the ditch.

 

 

Output

For each case, output a single integer, the maximum rate at which water may emptied from the pond.

 

 

Sample Input

5 4 1 2 40 1 4 20 2 4 20 2 3 30 3 4 10

 

 

Sample Output

50

 

 

Source

USACO 93

  EK的模板提，由于数据不大用邻接矩阵就过了，EK算法感觉就是利用bfs不断寻找增广路，关键在于每找到一条增广路时要加上反向边，为了给返回的机会，也就是退流的过程，这儿我还是有点迷糊，不知道如何证明可行性= =。

 关于这个反向边，一种说法是给程序一个反悔的机会，看了好多博客我难以理解为何可以这么做，参考紫书上的说法感觉更易理解。EK算法实际上就是在残量网络上寻找增广路，残量也就是残余容量，即容量与流量之差，c(u,v)-f(u,v)。假如c(u,v)=16,f(u,v)=11,那么r(u,v)=c(u,v)-f(u,v)=5,r(v,u)=c(v,u)-f(v,u)=0-(-11)=11,因为v,u之间实际并无边，所以容量就可以认为是0，又f(u,v)=-f(v,u)满足斜对称性。这就是加入反向边的正确性。

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
int cap[220][220];
int a[220],p[220];
int n,m;
int bfs(int s,int t)
{
    queue<int>q;
    memset(p,-1,sizeof(p));
    q.push(s);
    a[s]=inf;
    p[s]=0;
    while(!q.empty()){
        int u=q.front();q.pop();
        if(u==t)break;
        for(int i=1;i<=n;++i)
        {
            if(i!=s&&cap[u][i]>0&&p[i]==-1){
                p[i]=u;
                a[i]=min(cap[u][i],a[u]);
                q.push(i);
            }
        }
    }
    if(p[t]==-1)return -1;
    return a[t];
}
int maxflow(int s,int t)
{
   int ret=0,delta=0;
   while((delta=bfs(s,t))!=-1){
    int k=t;
    while(k!=s){
        int las=p[k];
        cap[las][k]-=delta;
        cap[k][las]+=delta;
        k=p[k];
    }
    ret+=delta;
   }
   return ret;
}
int main()
{
    int i,j,k;
    int u,v,w;
    while(cin>>m>>n){
        memset(cap,0,sizeof(cap));
        memset(a,0,sizeof(a));
        for(i=1;i<=m;++i){
            cin>>u>>v>>w;
            if(u==v)continue;
            cap[u][v]+=w;
        }
        cout<<maxflow(1,n)<<endl;
    }
    return 0;
}

 

 

 

　　贴上一发DINIC算法的，数据不大所以看不出来二者的时间差异。

DINIC算法先跑bfs对点进行分层，然后逐层跑阻塞流来增广。

      当前边优化,用一个cur[u]记录u点当前遍历到那一条边了，下一次再访问到u的时候直接从上一次记录的

边开始遍历，减少很多遍历的时间。因为已经访问过的边肯定已经满了(最大化)所以不必要再访问了。

        多路增广，当前弧优化，炸点。

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int maxn=220;
struct Edge
{
  int v,cap,flow,next;
}e[maxn<<1];
int first[maxn],d[maxn],cur[maxn],tot,N,M;
bool vis[maxn];
void add(int u,int v,int cap,int flow){
  e[tot]=Edge{v,cap,flow,first[u]};
  first[u]=tot++;
}
bool bfs(){
    memset(vis,0,sizeof(vis));
    memset(d,0,sizeof(d));
    queue<int>q;
    q.push(1);
    d[1]=0;
    vis[1]=1;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=first[u];~i;i=e[i].next){
           if(!vis[e[i].v]&&e[i].cap>e[i].flow){
            vis[e[i].v]=1;
            d[e[i].v]=d[u]+1;
            q.push(e[i].v);
           }
        }
    }
    return vis[N];
    
}
int dfs(int u,int a){
    if(u==N||a==0) return a;
    int flow=0,f;
    for(int &i=cur[u];~i;i=e[i].next){
        if(d[e[i].v]==d[u]+1 && (f=dfs(e[i].v,min(a,e[i].cap-e[i].flow)))>0){
            e[i].flow+=f;
            e[i^1].flow-=f;
            flow+=f;
            a-=f;
            if(!a) break;
        }
    }
    return flow;
}
void solve(){
   int ans=0;
   while(bfs()){
      for(int i=1;i<=N;++i) cur[i]=first[i];
      ans+=dfs(1,inf);
   }
   printf("%d\n",ans);
}
int main(){
  while(scanf("%d%d",&M,&N)!=EOF){
    tot=0;
    memset(first,-1,sizeof(first));
    int u,v,w;
    while(M--){
      scanf("%d%d%d",&u,&v,&w);
      add(u,v,w,0);
      add(v,u,0,0);
    }
    solve();
  }
  return 0;
}
/*
5 4
1 2 40
1 4 20
2 4 20
2 3 30
3 4 10
*/