实验四 图的实现与应用
课程名称:《程序设计与数据结构》
学生班级:1623班
学生姓名:朱娅霖
学生学号:20162322
实验时间:2017年11月20日—2017年11月24日
实验名称:图的实现与应用
指导老师:娄嘉鹏、王志强老师
0.目录
- [图的实现与应用-1](#1) - [图的实现与应用-2](#2) - [图的实现与应用-3](#3)图的实现与应用-1
### 一、实验要求 > **用邻接矩阵实现无向图**(边和顶点都要保存),实现在包含`添加和删除结点的方法`,`添加和删除边的方法`,`size()`,`isEmpty()`,`广度优先迭代器`,`深度优先迭代器` 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
1. 邻接矩阵:图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
2. 用邻接矩阵实现无向图
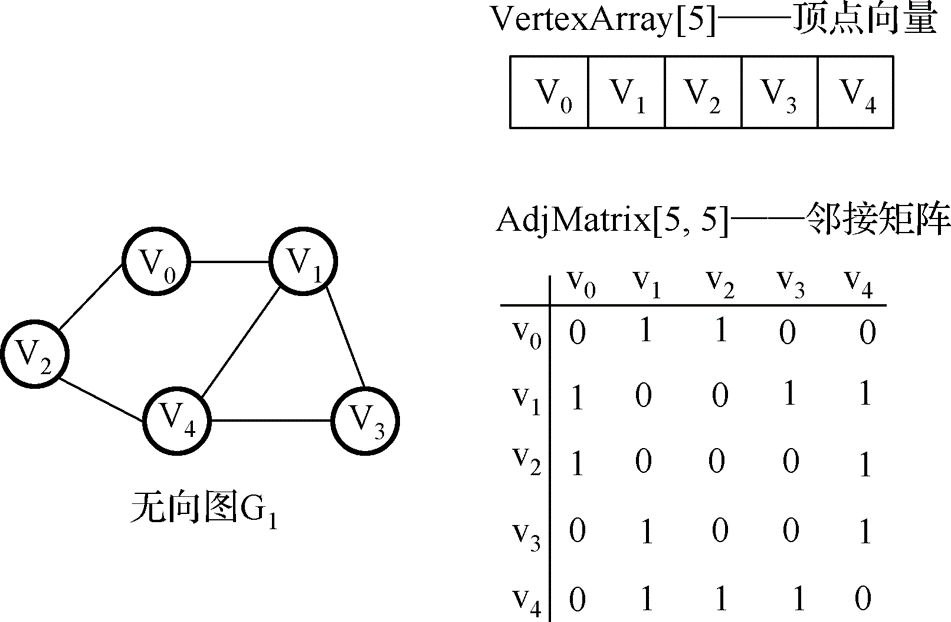
无向图的邻接矩阵对称,可压缩存储;
无向图中顶点 vi 的度是邻接矩阵中第 i 行 1 的个数。
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似,简称DFS。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。显然,深度优先搜索是一个递归的过程。
广度优先搜索算法(Breadth First Search),又称为"宽度优先搜索"或"横向优先搜索",简称BFS。
它的思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2...的顶点。
三、实验结果
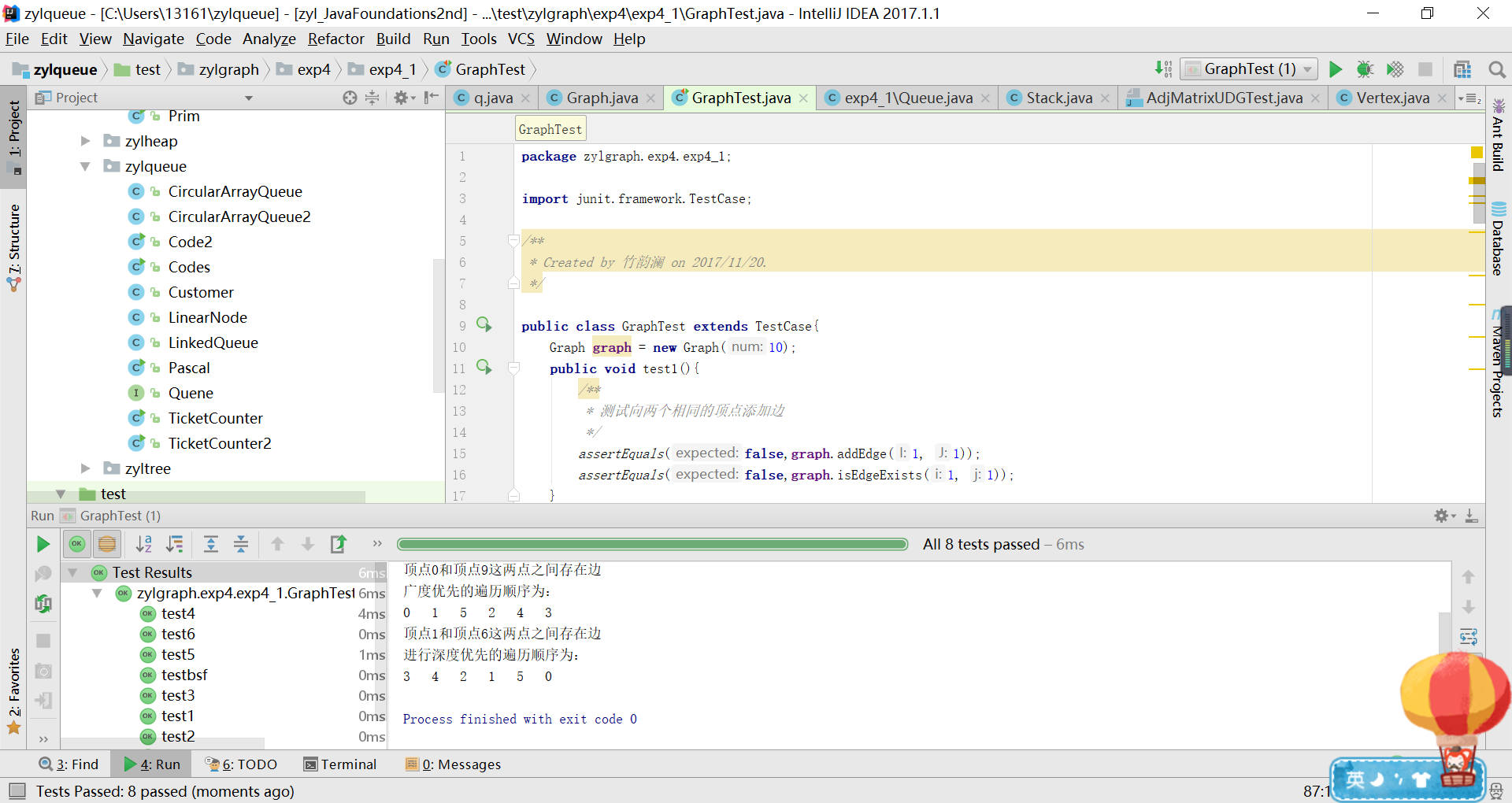
四、代码链接
MatrixGraph.java
Queue.java
Stack.java
GraphTest.java
图的实现与应用-2
### 一、实验要求 > **用十字链表实现无向图**(边和顶点都要保存),实现在包含`添加和删除结点的方法`,`添加和删除边的方法`,`size()`,`isEmpty()`,`广度优先迭代器`,`深度优先迭代器` 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
1. 十字链表:十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
2. 无向图的深度优先与广度优先
三、实验结果
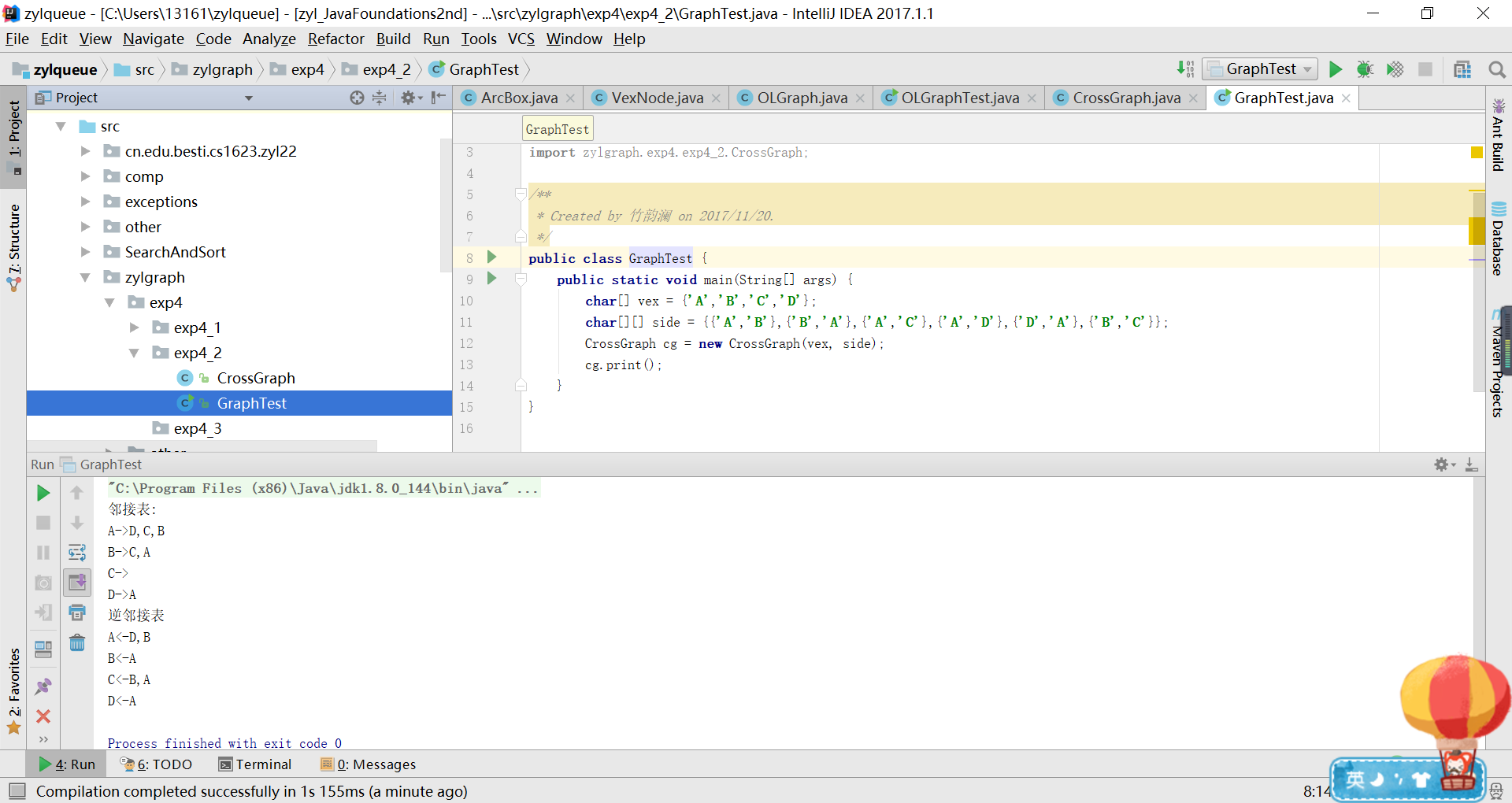
代码链接
图的实现与应用-3
### 一、实验要求 > 实现PP19.9 >> 创建计算机网络路由系统,输入网络中点到点的线路,以及每条线路使用的费用,系统输出网络中各点之间最便宜的路径,指出不相通的所有位置。 > > 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
- 创建此计算机网络路由系统及最短路径问题
- 此处使用Floyd算法,详情见图(二)——最小生成树、最短路径问题
三、实验结果
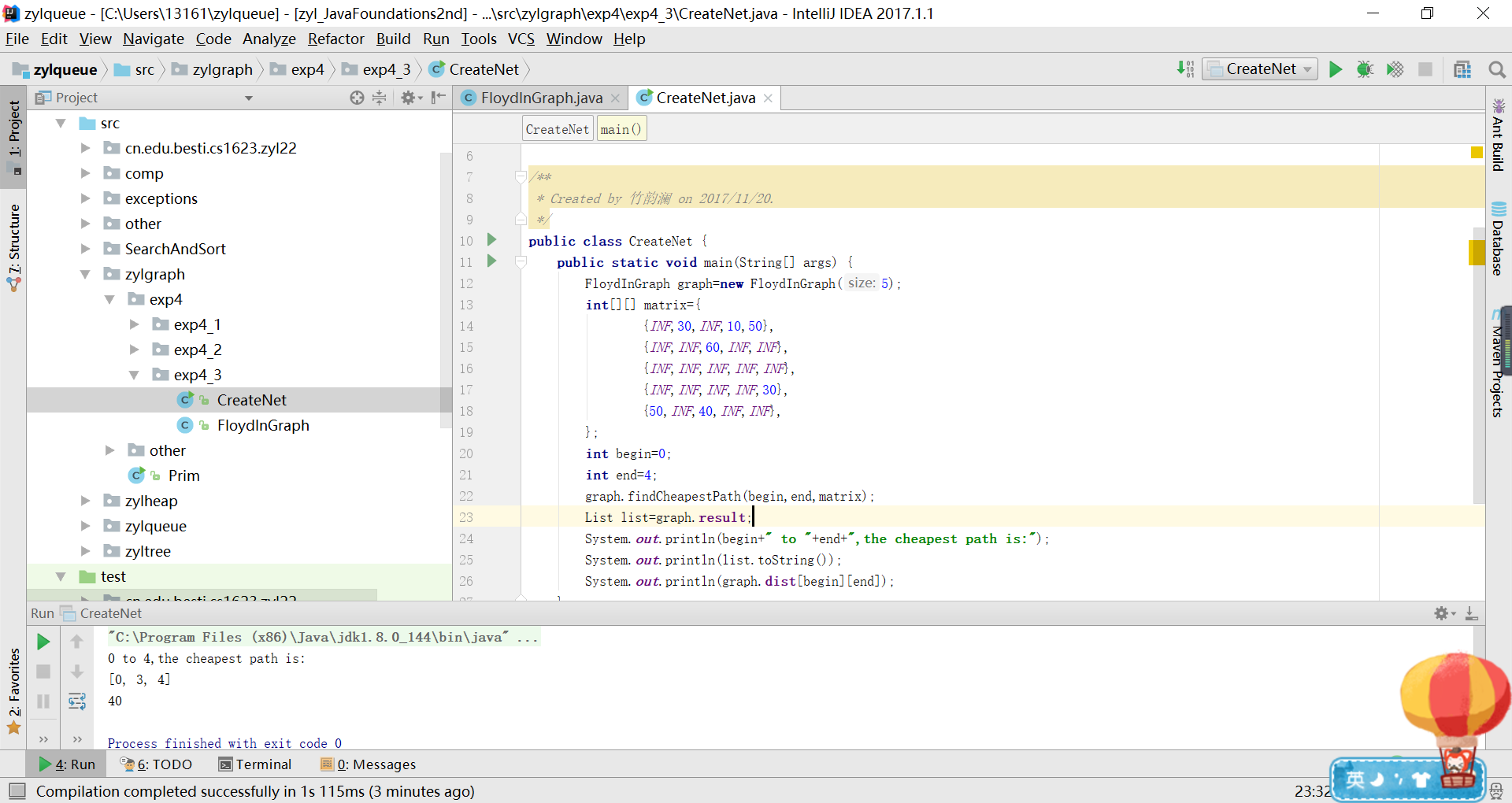
四、代码链接
---恢复内容结束---
# 实验四 图的实现与应用0.目录
- [图的实现与应用-1](#1) - [图的实现与应用-2](#2) - [图的实现与应用-3](#3)图的实现与应用-1
### 一、实验要求 > **用邻接矩阵实现无向图**(边和顶点都要保存),实现在包含`添加和删除结点的方法`,`添加和删除边的方法`,`size()`,`isEmpty()`,`广度优先迭代器`,`深度优先迭代器` 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
1. 邻接矩阵:图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
2. 用邻接矩阵实现无向图

无向图的邻接矩阵对称,可压缩存储;
无向图中顶点 vi 的度是邻接矩阵中第 i 行 1 的个数。
图的深度优先搜索(Depth First Search),和树的先序遍历比较类似,简称DFS。
它的思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。显然,深度优先搜索是一个递归的过程。
广度优先搜索算法(Breadth First Search),又称为"宽度优先搜索"或"横向优先搜索",简称BFS。
它的思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2...的顶点。
三、实验结果

四、代码链接
MatrixGraph.java
Queue.java
Stack.java
GraphTest.java
图的实现与应用-2
### 一、实验要求 > **用十字链表实现无向图**(边和顶点都要保存),实现在包含`添加和删除结点的方法`,`添加和删除边的方法`,`size()`,`isEmpty()`,`广度优先迭代器`,`深度优先迭代器` 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
1. 十字链表:十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
2. 无向图的深度优先与广度优先
三、实验结果

代码链接
图的实现与应用-3
### 一、实验要求 > 实现PP19.9 >> 创建计算机网络路由系统,输入网络中点到点的线路,以及每条线路使用的费用,系统输出网络中各点之间最便宜的路径,指出不相通的所有位置。 > > 给出伪代码,产品代码,测试代码(不少于5条测试) 上方提交代码链接 附件提交测试截图二、实验内容
- 创建此计算机网络路由系统及最短路径问题
- 此处使用Floyd算法,详情见图(二)——最小生成树、最短路径问题
三、实验结果





