20162322 2017-2018-1 《程序设计与数据结构》第十周学习总结
教材学习内容总结
理解图与有向图、无向图
理解带权图
会应用带权图
理解图的广度优先遍历和深度优先遍历
掌握最小生成树算法
掌握图的实现
基本定义
一个图(Graph)是一个序偶<V, E>,记为G = <V, E>,其中:
(1)V = {v1, v2, …, vn}是有限非空集合,vi称为结点,V称为结点集。
(2)E是有限集合,称为边集。E中的每个元素都是V中顶点偶对,称之为边。
序偶:以规定的次序排列的两个对象a和b。<a,b> = <c, d> iff a=c,b=d
图的表示:
- 集合表示:对于一个图G,如果将其记为G = <V, E>,并写出V和E的集合表示,称为图的集合表示。
- 图形表示:用小圆圈表示V中的结点,用由u指向v的有向线段表示有向边<u, v>;无向线段表示无向边(u, v),称为图的图形表示。
图的分类:
- 无向图(undirected gragh)
表示边的顶点对是无序的图是无向图,即如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。 - 有向图(directed gragh)
图中的边是顶点的有序对的图标为有向图。 - 带权图(weighted gragh)
图的每条边都对应一个权值的图成为带权图。
图的存储结构及实现
邻接矩阵
假设图G=(V, E)有n个顶点,则邻接矩阵AdjMatrix是一个n×n的方阵,定义为

当图带权时,则为

无向图邻接矩阵:
- 无向图的邻接矩阵对称,可压缩存储;
- 无向图中顶点 vi 的度是邻接矩阵中第 i 行 1 的个数。
有向图邻接矩阵:
- 有向图邻接矩阵不一定对称;
- 有向图中
- 顶点 vi 的出度是邻接矩阵中第 i 行 1 的个数。
- 顶点 vi 的入度是邻接矩阵中第 i 列 1 的个数。
邻接表
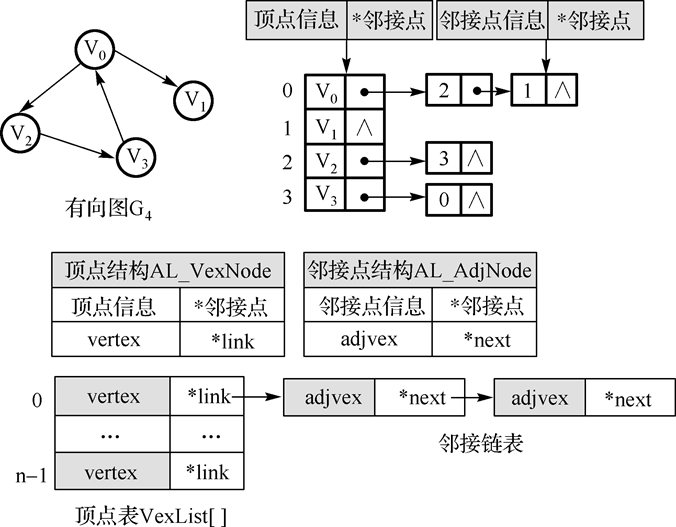
十字链表
详见十字链表
图的遍历
广度优先
类比树的遍历中的层序遍历,运用队列实现,能找到最短路径,但所需空间大
深度优先
类比树的遍历中的先序、中序、后序遍历,运用栈实现,难以寻找最优解,但内存消耗小。
最小生成树
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
课下测试(CH17,CH18)
1. 当向二叉查找树添加新元素时,该元素被添加为_______
A. 内部节点
B. 子树
C. 叶
D. 根
E. 以上都不是
正确答案:D 我的答案:C
添加到二叉查找树中的元素将作为叶子添加,答案错误。
2. 将元素添加到堆中时,以下哪项总是正确的?
A. 新元素将永远是一片叶子
B. 新元素将永远是根
C. 新的元素将永远是一个内部节点
D. 新元素将永远有2个孩子
E. 以上都不是正确的
正确答案:E 我的答案:A
向堆中添加元素时,可能会在树中的**任何位置**结束。
3. 堆排序通过从中构建一个堆来排序元素,然后从根中一次删除一个元素(判断)
A. true
B. false
正确答案:B
堆排序使用堆属性通过构建堆中的堆来排序元素,然后逐个删除它们。
结对及互评
点评:
-
博客中值得学习的或问题:
- xxx
- xxx
-
代码中值得学习的或问题:
- xxx
- xxx
-
其他
本周结对学习情况
- 20162323
- 结对照片
- 结对学习内容
- XXXX
- XXXX
其他(感悟、思考等,可选)
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 20/20 | 绪论 |
| 第二周 | 386/386 | 0/1 | 20/40 | |
| 第三周 | 500/886 | 2/3 | 20/60 | 选择与排序、团队作业一(一) |
| 第四周 | 300/1186 | 2/4 | 20/80 | 实验一(线性结构)、线性表、团队作业一 (二) |
| 第五周 | 300/1486 | 2/6 | 20/100 | 栈、团队作业二 |
| 第六周 | 300/1786 | 2/8 | 20/120 | 队列、团队作业三 |
| 第七周 | 844/2630 | 3/11 | 20/140 | 树 |
| 第八周 | 544/3174 | 2/13 | 20/160 | 实验二(树)、二叉查找树 、团队作业四和五(一) |
| 第九周 | 375/3645 | 2/15 | 20/180 | 哈夫曼树、堆和优先队列 、团队作业四和五(二) |
| 第十周 | 1484/4813 | 5/19 | 30/210 | 实验三(查找与排序)、图 、《构建之法》第一章阅读 |
-
计划学习时间:25小时
-
实际学习时间:30小时
-
改进情况:多思考!多思考!




