学号 2017-2018-1 《程序设计与数据结构》第三周学习总结
教材学习内容总结
查找(Searching)
线性查找(linear search)
属于无序查找算法,适合于存储结构为顺序存储或链接存储的线性表。
基本思想:从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
时间复杂度:O(n)
代码实现:
//-------------------------------------------------------------------------
// Searches the specified array of objects using a linear search 线性查找
// algorithm. Returns null if the target is not found.
//-------------------------------------------------------------------------
public static Comparable linearSearch (Comparable[] data,
Comparable target) {
Comparable result = null;
int index = 0;
while (result == null && index < data.length){
if (data[index].compareTo(target) == 0)
result = data[index];
index++;
}
return result;
}
二分查找(binary search)
属于有序查找算法,元素必须是有序的,如果是无序的则要先进行排序操作。
基本思想:用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
时间复杂度:O(log2n)
代码实现:
//--------------------------------------------------------------------------
// Searches the specified array of objects using a binary search 二分查找
// algorithm. Returns null if the target is not found.
//--------------------------------------------------------------------------
public static Comparable BinarySearch(Comparable[] data,
Comparable target){
Comparable result = null;
int first = 0, last = data.length-1, mid;
while (result == null && first <= last){
mid = (first + last) / 2; // determine midpoint
if (data[mid].compareTo(target)==0)
result = data[mid];
else
if (data[mid].compareTo(target) > 0)
last = mid - 1;
else
first = mid + 1;
}
return result;
}
排序(Sorting)
选择排序(selection sort)
基本思想:每一趟排序选择出最小的(或者最大的)值,顺序放在已排好序的数列的后面。
时间复杂度:O(n^2)
代码实现:
//-----------------------------------------------------------------
// Sorts the specified array of integers using the selection
// sort algorithm.
//-----------------------------------------------------------------
public static void selectionSort (Comparable[] data)
{
int min;
for (int index = 0; index < data.length-1; index++)
{
min = index;
for (int scan = index+1; scan < data.length; scan++)
if (data[scan].compareTo(data[min]) < 0)
min = scan;
swap (data, min, index);
}
}
插入排序(insertion sort)
基本思想:将一个记录插入到一个已排好序的有序表中,从而得到一个新的、记录增1的有序表。默认将第一个元素看为有序表,然后依次插入后边的元素。
时间复杂度:O(n^2)
代码实现:
//-----------------------------------------------------------------
// Sorts the specified array of objects using an insertion
// sort algorithm.
//-----------------------------------------------------------------
public static void insertionSort (Comparable[] data)
{
for (int index = 1; index < data.length; index++)
{
Comparable key = data[index];
int position = index;
// Shift larger values to the right
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
}
data[position] = key;
}
}
冒泡排序(bubble sort)
属于交换排序
基本思想:重复走访过要排序的序列,一次比较两个元素,如果他们的顺序错误就将他们进行交换,一次冒上来的是最小的,其次是第二小。
时间复杂度:O(n^2)
代码实现:
//-----------------------------------------------------------------
// Sorts the specified array of objects using a bubble sort
// algorithm.
//-----------------------------------------------------------------
public static void bubbleSort (Comparable[] data)
{
int position, scan;
for (position = data.length - 1; position >= 0; position--)
{
for (scan = 0; scan <= position - 1; scan++)
if (data[scan].compareTo(data[scan+1]) > 0)
swap (data, scan, scan+1);
}
}
快速排序(quick sort)
基本思想:通过一趟排序将待排序列分割成两个部分,其中一部分记录关键字均比另一部分记录的关键字小,则可以分别对这两部分关键字继续排序,以达到整个序列有序的目的。
时间复杂度:O(nlgn)
代码实现:
//-----------------------------------------------------------------
// Sorts the specified array of objects using the quick sort
// algorithm.
//-----------------------------------------------------------------
public static void quickSort (Comparable[] data, int min, int max)
{
int pivot;
if (min < max)
{
pivot = partition (data, min, max); // make partitions
quickSort(data, min, pivot-1); // sort left partition
quickSort(data, pivot+1, max); // sort right partition
}
}
//-----------------------------------------------------------------
// Creates the partitions needed for quick sort.
//-----------------------------------------------------------------
private static int partition (Comparable[] data, int min, int max)
{
// Use first element as the partition value
Comparable partitionValue = data[min];
int left = min;
int right = max;
while (left < right)
{
// Search for an element that is > the partition element
while (data[left].compareTo(partitionValue) <= 0 && left < right)
left++;
// Search for an element that is < the partitionelement
while (data[right].compareTo(partitionValue) > 0)
right--;
if (left < right)
swap(data, left, right);
}
// Move the partition element to its final position
swap (data, min, right);
return right;
}
归并排序(merge sort)
基本思想:归并排序是将两个或两个以上的有序表组合成一个有序表,该算法是采用分治法实现
时间复杂度:O(nlgn)
代码实现:
//-----------------------------------------------------------------
// Sorts the specified array of objects using the merge sort
// algorithm.
//-----------------------------------------------------------------
public static void mergeSort (Comparable[] data, int min, int max)
{
if (min < max)
{
int mid = (min + max) / 2;
mergeSort (data, min, mid);
mergeSort (data, mid+1, max);
merge (data, min, mid, max);
}
}
//-----------------------------------------------------------------
// Sorts the specified array of objects using the merge sort
// algorithm.
//-----------------------------------------------------------------
public static void merge (Comparable[] data, int first, int mid,
int last)
{
Comparable[] temp = new Comparable[data.length];
int first1 = first, last1 = mid; // endpoints of first subarray
int first2 = mid+1, last2 = last; // endpoints of second subarray
int index = first1; // next index open in temp array
// Copy smaller item from each subarray into temp until one
// of the subarrays is exhausted
while (first1 <= last1 && first2 <= last2)
{
if (data[first1].compareTo(data[first2]) < 0)
{
temp[index] = data[first1];
first1++;
}
else
{
temp[index] = data[first2];
first2++;
}
index++;
}
// Copy remaining elements from first subarray, if any
while (first1 <= last1)
{
temp[index] = data[first1];
first1++;
index++;
}
// Copy remaining elements from second subarray, if any
while (first2 <= last2)
{
temp[index] = data[first2];
first2++;
index++;
}
// Copy merged data into original array
for (index = first; index <= last; index++)
data[index] = temp[index];
}
教材学习中的问题和解决过程
快速排序的一般策略是:先选择表中的一个元素作为划分元素。接下来,对表进行划分,小于划分元素的所有元素放到划分元素的左侧,大于划分元素的所有元素放到它的右侧。最后,再用这个快速排序的策略(递归地)对两个划分段进行划分。
如果初始时待排序的项是随机排列的,则任意选取划分元素,可以由表中的第一个元素担当。从效率角度考虑,如果划分元素能把表划分为大致相等的两部分最好了,不过无论如何选择划分元素,算法都能正确进行。
进一步学习:
书中的代码中是固定以第一个元素为划分元素,这样若输入几乎有序,在每次迭代的过程中,输入将被极其不均匀的划分,导致算法性能差。我就想,有没有什么方法可以解决这一问题?于是我查到一种普遍的方法,即选取第一,中间,最后元素的中值作为划分元素。这样就能在只添加几行if条件代码,不花费太多时间和空间的情况下,有效增加提高效率的几率。
代码调试中的问题和解决过程
-
问题1:
我的IDEA突然出了以下问题:
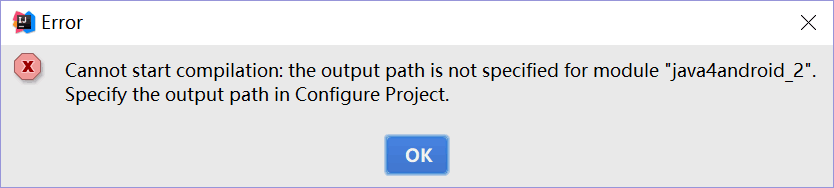
-
问题1解决方案
按照链接中的方法,调整设置
代码托管
结对及互评
- 学习很努力,态度很认真,但需注意改变方法,提高效率。
本周结对学习情况
- 20162323
- 结对照片
- 结对学习内容
- 上课讲义学习
其他(感悟、思考等,可选)
本周的学习任务很多,本周的学习效率略低,合理的时间安排很重要。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 1/1 | 20/20 | 了解算法与数据结构 |
| 第二周 | 300/500 | 0/1 | 20/40 | 泛型 |
| 第三周 | 500/1000 | 3/4 | 25/65 | 查找与排序 |
-
计划学习时间:15小时
-
实际学习时间:25小时
-
改进情况:



