hdu5444Elven Postman（主席树思想的应用）

主席树这个概念应该不陌生吧！恩？不会， 戳这里。

主席树（函数式线段树）用的是函数思想，一个节点开数组用来保存自己的左右节点，这样节省许多不必要的空间，还可以保存许多历史状态。而这里我们用的是主席树的函数思想来实现。

上题：http://acm.hdu.edu.cn/showproblem.php?pid=5444

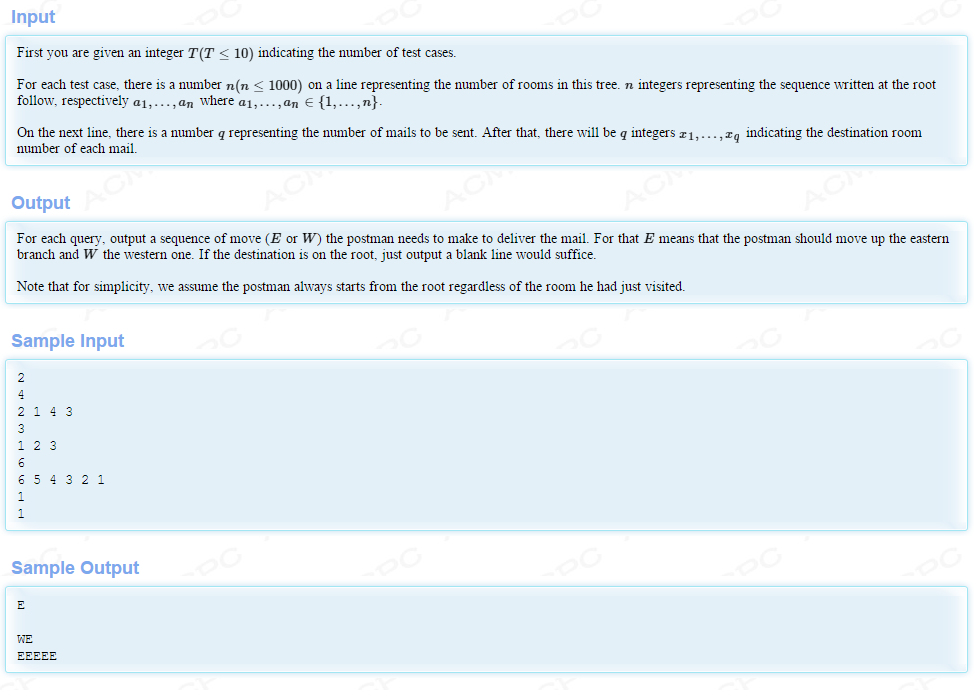
题目大意：

给你一个序列，第一个数为二叉树根节点，之后每个数往上加节点，且保证左节点小于根节点，且保证右节点大于根节点。且每个节点最多有2个子节点。然后再查询位置，每往左找输出一个E，右找输出W。例如序列2， 1， 4， 3可以生成如下图：

 

例如查找1，需要往左一次输出E，查找2,不需要搜直接输出，查找3需要向右一次再向左一次，输出WE。

哇！这题好水，不就是二叉树吗？啪啪啪，几分钟码完了， 交一发，嗯，居然RE了，不行，的开大叔组，开成10W，嗯？又RE了。最后一想如果这个数列是1-n，即a[i] = i,那样需要访问到2的1000次方个节点。咕~~(╯﹏╰)b，郁闷呢，然后回想起以前学过的主席树，可以开数组记录该节点的左右儿子，那样岂不是只要访问到n个节点就行。然后就这样AC了。（比赛的时候提交的时候超了了51s，，14:00:51的时候提交的。本来能AC的，TAT）

附上代码：

 

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 4000 + 5;

int a[N], b[N],ls[N], rs[N], mx[N];

int n, k, tot, sz, ql, qr, x, q, T;

void update(int o, int l, int r, int p){
    int m = (l + r) >> 1;
    if(p <= mx[o]){
        if(ls[o] == 0){
            ls[o] = tot;
            mx[tot] = p;
            return ;
        }
        else update(ls[o], l, m, p);
    }
    else {
        if(rs[o] == 0){
            rs[o] = tot;
            mx[tot] = p;
            return;
        }
        else update(rs[o], m + 1, r, p);
    }
}

void query(int o, int l, int r, int k){
    if(mx[o] == k)return ;
    int m = (l + r) >> 1;
    if(k <= mx[o]){
        printf("E");
        query(ls[o], l, m, k);
    }
    else{
        printf("W");
        query(rs[o], m + 1, r, k);
    }
}

void work(){
    scanf("%d", &x);
    query(1, 1, n, x);
    puts("");
}

int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        tot = 1;
        //Build(rt[0], 1, n);
        memset(mx, 0, sizeof(mx));
        memset(ls, 0, sizeof(ls));
        memset(rs, 0, sizeof(rs));
        //for(int i = 1; i <= n; i ++)ls[i] = i << 1, rs[i] = i << 1|1;
        //for(int i = 0; i <= 20; i ++)printf("i = %d, rt = %d, ls = %d, rs= %d, mx = %d\n", i, rt[i], ls[i], rs[i], mx[i]);
        for(int i = 1; i <= n; i ++){
            scanf("%d", a + i);
            if(i == 1)mx[1] = a[1];
            else update(1, 1, n, a[i]);
            tot ++;
        }
        scanf("%d", &q);
        while(q --)work();
    }
    return 0;
}