2017 软工第二次作业
作业地址
GitHub地址 https://github.com/zyccccla/myWorks
项目需求
- 随机生成N个不重复的已解答完毕的数独棋盘
解题思路
- 刚开始拿到这道题目确实有一点晕,自己最开始想的也是通过随机或者暴力的方法一个个填入,看了网上的一些博客发现大多使用回溯法和全排列法,与N皇后问题有些类似,只不过数独多了一些判断条件。最终我决定使用回溯法来解决。附一个帮助我理解n皇后问题的博客
http://blog.csdn.net/hackbuteer1/article/details/6657109
最初一直卡在怎么输出多解的问题上,因为自己算法基础太薄弱,又回头去复习了一遍dfs算法,找到了两篇觉得不错的博客
http://helloitworks.com/678.html#more-678 探讨了dfs的通用解法
http://blog.csdn.net/raphealguo/article/details/7560918
后来终于找到了问题所在,我在dfs探索到一条结果时并没有继续从它的相邻节点继续探索从而导致无法输出多解(现在想想真是在上面耗了太多时间...)
主要代码
程序主要有3个函数,分别负责输出、检查和回溯
void printSudoku()
{
int x,y;
for(x=0;x<9;++x)
{
for(y=0;y<9;++y)
{
cout << map[x][y] <<' ';
}
cout << endl;
}
cout<<endl;
}
bool isValid(Pos p, int n)
{
int curRow = p.row; //验证行、列
int curCol = p.col;
for (int i = 0; i < 9; i++) {
if (map[i][curCol]==n || map[curRow][i]==n) {
return false;
}
}
int m = curRow / 3 * 3; //验证九宫格
int r = curCol / 3 * 3;
for(int j = m; j < m + 3;++j){
for(int k = r; k < r+3; ++k){
if(map[j][k]==n){
return false;
}
}
}
return true;
}
void solve(qpos & Q)
{
if (Q.empty()) { //递归结束条件
if(num<n)
{
num++;
printSudoku();
return;
}
}
Pos pos_now(Q.front().row, Q.front().col);
Q.pop_front();
for (int i = 1; i <= 9; i++) {
if (isValid(pos_now, i) ) {
map[pos_now.row][pos_now.col] = i; // 合法,则放置数字
solve(Q);
map[pos_now.row][pos_now.col] = 0; // 回溯
}
}
Q.push_front(pos_now); // 都不符合,返回
}
测试
-
运行测试


-
效能分析
虽然阅读了《构建之法》里单元测试的内容,对其有了一定了解,但是自己弄的还是时候还是很迷,加上插件也弄了半天弄不好,所以决定先做性能分析的内容 n设定为5000

 果然还是回溯的函数用了太多时间,因为把重心都放在了前期,改进优化就有些来不及了,后面我会深入的思考后 再来补上
-
psp表格
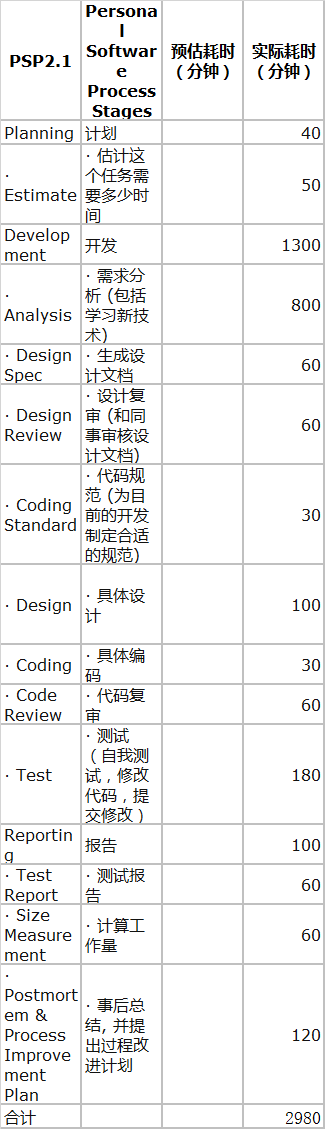
-
总结
虽然学到了很多新知识,不过感觉自己还是太拖拉了,导致后期十分仓促,以后要吸取这个教训,一开始就进行准备



