luoguP3366 【模板】最小生成树 x
-
- 2.4K通过
- 6.3K提交
- 题目提供者HansBug
- 标签 云端↑ 生成树
- 难度 普及-
- 时空限制 1s / 128MB
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
输入样例#1:
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
输出样例#1:
7
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
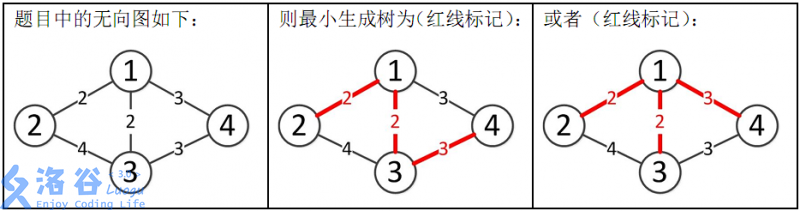
所以最小生成树的总边权为2+2+3=7
思路:
首先这道题是求最小生成树的模板,求最小生成树的办法有2种:
1)prim
2)kruskal
坑点:
1)记住要判断什么时候输出“orz”
2)在使用prim算法的时候,我使用的是邻接矩阵,不清楚你们用的什么,在邻接矩阵进行输入的时候,一定要进行判断一下在进行赋值!!
数据中有重边!!数据中有重边!!数据中有重边!!需要选取较小的一条,即算法中已经被选出来的节点不用再次进行赋值。
调了2天qwq,血的教训qwq(还有这种操作吗???orz)
上代码:
1)prim
在网页上找了不少题解后,突然发现,还是kruskal比较好理解。。。
写prim的有各式各样的2333
我就写了一种嘻嘻
#include <iostream> #include <cstdio> #define Maxx 0x7fffffff using namespace std; const int M = 5050; int n,m; //n=顶点的个数,m=边的个数 int edge[M][M]={ /*输入的邻接矩阵*/ }; int lowcost[M]; //记录Vnew中每个点到V中邻接点的最短边 bool visited[M]; //标记某点是否加入Vnew int pre[M]; //记录V中与Vnew最邻近的点 void prim(int start) { int sumweight=0,i,j,k=0; visited[start]=true; for(i=1;i<=n;i++) { lowcost[i]=edge[start][i]; pre[i]=start; } int minn=Maxx; //最小权值 int v=-1; //所对应的下标 for(i=1;i<n;i++) //进行n-1次,因为此时已经知道当前start点到另一点距离最短 { minn=Maxx; for(j=1;j<=n;j++) { if(visited[j]==false && lowcost[j]<minn) //在Vnew之外寻找最短路径 { minn=lowcost[j]; //最短路径 v=j; } } // printf("%d %d %d\n",pre[v],v,lowcost[v]); if(v==-1) { cout<<"orz"<<endl; return; } visited[v]=true; //将v加Vnew中 sumweight+=lowcost[v]; //计算路径长度之和 for(j=1;j<=n;j++) { if(visited[j]==false && edge[v][j]<lowcost[j]) { lowcost[j]=edge[v][j]; //此时v点加入Vnew 需要更新lowcost pre[j]=v; } } } // printf("the minmum weight is %d",sumweight); //进行输出 printf("%d",sumweight); } int main() { scanf("%d%d",&n,&m); for(int i=1; i<=n; i++) { // lowcost[i]=Maxx; for(int j=1; j<=n; j++) edge[i][j]=Maxx; //初始化图 } int x,y,w,s,Max=Maxx; for(int k=1; k<=m; k++) { cin>>x>>y>>w; if(w<edge[x][y]) edge[x][y]=edge[y][x]=w; //构建图 if(w<Max) { Max=w; s=x; //寻找最初最"实惠"的点 } } prim(s); //进行求解最小生成树 return 0; }
2)kruskal
#include <algorithm> #include <iostream> #include <cstdio> using namespace std; const int N = 5010; const int M = 200020; int n,m,ans; int dad[N]; struct A { int u,v,w; bool operator < (const A &qwq)const { return w < qwq.w; } }t[M]; int getdad(int x) { return dad[x] == x ? x : dad[x] = getdad( dad[x] ); } void kruskal() { sort(t+1,t+1+m); for(int i=1;i<=m;i++) { int f1=getdad(t[i].u),f2=getdad(t[i].v); if(f1!=f2) { dad[f1]=f2; ans+=t[i].w; } } int tmp=getdad(1); for(int i=2;i<=n;i++) { if(getdad(i)!=tmp) { printf("orz"); return; } } printf("%d\n",ans); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;i++) scanf("%d%d%d",&t[i].u,&t[i].v,&t[i].w); for(int i=1;i<=n;i++) dad[i]=i; kruskal(); return 0; }

