luogu P1314 聪明的质监员 x

P1314 聪明的质监员(至于为什么选择这个题目,可能是我觉得比较好玩呗)

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 n 个矿石，从 1到n 逐一编号，每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是：

1 、给定m 个区间[Li,Ri]；

2 、选出一个参数 W；

3 、对于一个区间[Li,Ri]，计算矿石在这个区间上的检验值Yi：

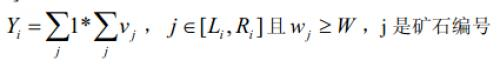
这批矿产的检验结果Y 为各个区间的检验值之和。即：Y1+Y2...+Ym

若这批矿产的检验结果与所给标准值S 相差太多，就需要再去检验另一批矿产。小T

不想费时间去检验另一批矿产，所以他想通过调整参数W 的值，让检验结果尽可能的靠近

标准值S，即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

输入文件qc.in 。

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n 行，每行2个整数，中间用空格隔开，第i+1 行表示 i 号矿石的重量 wi 和价值vi。

接下来的m 行，表示区间，每行2 个整数，中间用空格隔开，第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。

注意：不同区间可能重合或相互重叠。

输出格式：

输出文件名为qc.out。

输出只有一行，包含一个整数，表示所求的最小值。

输入输出样例

输入样例#1：

输出样例#1：

说明

【输入输出样例说明】

当W 选4 的时候，三个区间上检验值分别为 20、5 、0 ，这批矿产的检验结果为 25，此

时与标准值S 相差最小为10。

【数据范围】

对于10% 的数据，有 1 ≤n ，m≤10；

对于30% 的数据，有 1 ≤n ，m≤500 ；

对于50% 的数据，有 1 ≤n ，m≤5,000；

对于70% 的数据，有 1 ≤n ，m≤10,000 ；

对于100%的数据，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

思路+坑点:

　　二分答案+前缀和

　　1.首先来看给出公式,

　　　　公式含义:就是在说从Li到Ri区间之内的,中间的所有w值超过W的项的个数乘上这些(满足条件的)矿石的v的和就是我们求所要的Y啦!!!

　　2.因为W的值越大,得出的Y越小,是单调的,所以一点需要注意的是l跟r的变化什么的.

　　3.要求出的是那个离标准值最近的Y.而不是第一个大于等于或是第一个大于标准值的Y. (此Y非彼Y???)

　　4.分析一下题,可以得出W的值只需要在那一坨wi中取就好了,对结果是没有任何影响的

　　　　可是为什么呢?因为公式...

　　5.其实我们看到这个题,想到二分答案是不难的,但是如果就直接上二分答案,简单暴力地求和什么的,就会超时,时间复杂度O((m*n)log w). 你想啊,暴力的话,两个循环,时间复杂度完美的爆炸:差不多O(m*n)吧. 然后加上二分(log w)就是上面的复杂度了. 然后粗略计算极限数据,仅仅一个计算Y的函数差不多就会爆掉呢(可能吧,我看的dalao的博客).

　　6.处理前缀和的时候:

　　　　因为W是在不断变化的,所以只需要再重新更新一下前缀和就行. 差不多就是将满足条件的弄上,不行的丢掉吧,大概是这样.

　　7.时间复杂度:

　　　　应该是O((m+n)*log w)的复杂度(或者O(AC)). 这题就是个二分(log w(枚举的w嘛))+前缀和 (因为每个check函数中都有两个循环,一个循环到n,处理前缀和,循环到m求Y.(m个区间嘛~)

　　8.不开long long见祖宗, 多年OI一场空.

　　9.要取abs(ans-S)的最小值(绝对值哦!),不要只取ans-S的最小值(因为可能会出来负值),如果不的话的话当ans<S的时候就越小越赚便宜咯.

　　10.ans的初始化最大值要够!!!不要赋成0x77f什么的,(赋值为1e11差不多是可以的)这个最值(0x77f)对于其中35分的数据是不够大的,目测来看至少要到1e11吧,然后1e10会WA掉5个测试点(额..65分)呢,因为这个题会爆int,然而0x77f只是最大int.

代码:

///额...至于格式什么的,这个就随你便啦,不顺眼可以改嘛~
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long
using namespace std;
const int M = 2e5 + 233;

int n,m;
LL S;
///注意这里,S是long long型的,因为数据范围是到10^12嘛~ 
int w[M],v[M],L[M],R[M];
LL num[M],sum[M];
///num数组记录满足条件区间内个数.
///sum数组记录满足条件区间内对应的v值的和
int l=1e7,r=0;

LL Lmin(LL a,LL b)
{return a > b ? b : a;}

int max(int a,int b)
{return a > b ? a : b;}

LL check(int x)///注意返回值!!!!
{
    LL y=0,t=0,yy=0;
    /*
    for(int i=1;i<=m;i++)///O(m*n*log w)
    {
        y=0,t=0;
        for(int j=L[i];j<=R[i];j++)
         if(w[i]>=x) y+=v[j],t++;
        yy+=t*y;
    }
    */
    ///memset(sum,0,sizeof(sum));
    ///memset(num,0,sizeof(num));
    for(int i=1;i<=n;i++)///O((m+n)*log w)
    {
        sum[i]=sum[i-1];
        num[i]=num[i-1];///前缀和w 
        if(w[i]>=x) sum[i]+=v[i],num[i]++;
    }
    for(int i=1;i<=m;i++)
    {
        LL ss=sum[R[i]]-sum[L[i]-1];
        LL nn=num[R[i]]-num[L[i]-1];
        yy+=ss*nn;
    }
    return yy;
}

void works()
{
    int mid;
    LL ans=1e11;///极大数! 
    while(l<=r)///枚举w
    {///S-Y!!!
        mid=(l+r)>>1;
        LL Y=check(mid);
        if(Y<S)///尽可能地靠近嘛
         r=mid-1;
        ///w往小里找,使得Y尽可能更大
        if(Y>S)
         l=mid+1;///w往大里找,同理
        if(Y==S)///如果没有差别的话 
        {
            printf("0\n");
            return;
        }
        ans=Lmin(ans,abs(S-Y));
        ///注意这里的S-Y要取绝对值
    }
    printf("%lld\n",ans);
}

void reads()
{
    scanf("%d%d%lld",&n,&m,&S);
    for(int i=1;i<=n;i++)
     scanf("%d%d",&w[i],&v[i]),
     r=max(r,w[i]),l=min(l,w[i]);
     ///在此范围之内进行查找
    for(int i=1;i<=m;i++)
     scanf("%d%d",&L[i],&R[i]);
     ///区间什么的
    works();
}

int main()
{
    reads();
    return 0;
}