DP（第一版）

序

任何一种具有递推或者递归形式的计算过程，都叫做动态规划

　　　　如果你一开始学的时候就不会DP,那么你在考试的时候就一定不会想到用动态规划！

需要进行掌握的内容

　　1)DP中的基本概念

　　2)状态

　　3)转移方程：状态与状态之间的关系

　　4)无后效性

　　　　　　DP写代码的方式

　　　　　　　　1)For 　　2)记忆化搜索

　　　　　　　 两种转移的方式

　　　　　　　    1) 顺推 　　2)逆转 

　　　　　　 大致的几个过程:

　　　　　　1)根据题意划分阶段

　　　　　　2)根据阶段确定状态

　　　　　　3)根据状态书写方程

一些DP的种类

　　区间DP　　数位DP　　 状压DP 　　插头DP(out)　　 树形DP 　　背包　　 博弈论DP

 在这里简单说一下一维01背包为什么要逆序进行dp操作哦~

　　　　　　首先%%%zyh学姐，讲得好清楚qwq

　　其实差不多就是一句话的事，可是我可能说得有点啰嗦....

　　想一下如果你正序枚举的话，因为dp转移方程是dp[j]=max(dp[j],dp[j-v[i]]+w[i]);

　　如果你正序枚举的话，在你枚举后面的时候还会用到前面的dp数组，但是因为前面的已经更新过了，里面有可能是有数的，所以如果你再次选上这个物品的话，就会与前方所做相矛盾，会将该件物品选取多次，不符合01背包每个物品只选取一次的原则，所以基于此，我们必须逆序来枚举！

　　逆序的话，他所用到的前面的dp数组都为选上一次的状态，没有被更新过，所以要逆序。

　　over！

先来说一下一些很神的东西!

矩阵乘法!!!

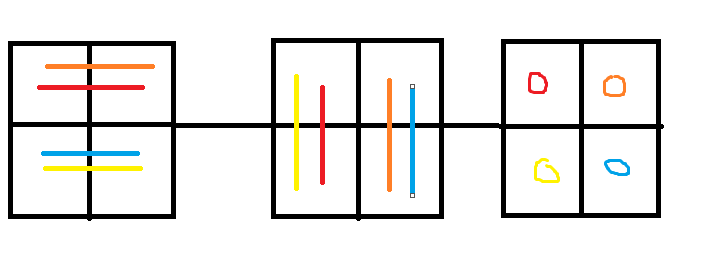
m1 i行*j列

m2 j行*k列

计算 m1*m2 的值

(计算后应该是 i行*k列的矩阵)

ps:矩阵乘法不具有交换律，但是具有结合律与分配律。

矩阵模板：

for (int a=1;a<=n;a++)
    for (int b=1;b<=m;b++)
        for (int c=1;c<=k;c++)
            m3[a][c]+=m1[a][b]*m2[b][c];

意为：

　　m3矩阵中a行c列的数就是把m1矩形的第1—a行中所有的数与m2矩形的第1—c列中所有的数分别进行对应相乘 然后加和.

例题：

f_i=f_i-1+2*f_i-2+3*f_i-3;

//i为下标

求f_n (其中n<=10^9)

(等我我做出来再发吧……QWQ)

给出一些练手的题:

1.codevs 1220 数字三角形

 时间限制: 1 s

 空间限制: 128000 KB

 题目等级 : 黄金 Gold

 

题目描述 Description

如图所示的数字三角形，从顶部出发，在每一结点可以选择向左走或得向右走，一直走到底层，要求找出一条路径，使路径上的值最大。

输入描述 Input Description

第一行是数塔层数N(1<=N<=100)。

第二行起，按数塔图形，有一个或多个的整数，表示该层节点的值，共有N行。

输出描述 Output Description

输出最大值。

样例输入 Sample Input

5

13

11 8

12 7 26

6 14 15 8

12 7 13 24 11

样例输出 Sample Output

86

数据范围及提示 Data Size & Hint

数字三角形

思路:

　　数字三角形使用DP,其实这就是一道模板题！(深搜也是可以过的啦~)

代码酱来也~

1)DP(for)

#include <iostream>
#define M 111

using namespace std;

int n,m[M][M];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>m[i][j];

    for(int i=n-1;i>=1;i--)
        for(int j=1;j<=i;j++)//逆序! 
            m[i][j]+=max(m[i+1][j],m[i+1][j+1]);

    cout<<m[1][1];

    return 0;
}

2)DP(记忆化DFS)

#include <iostream>//深搜
#include <cstdio>
#include <algorithm>
#define M 111

using namespace std;

int n;
int gg[M][M];
int v[M][M];

int dfs(int i,int j)
{
    if(v[i][j]==-1)//记忆化搜索
    {
        v[i][j]=gg[i][j]+max(dfs(i+1,j),dfs(i+1,j+1));
    }
    return v[i][j];
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
        {
            scanf("%d",&gg[i][j]);
            if(i == n) v[i][j]=gg[i][j];//将最后一行赋值
            else v[i][j]=-1; 
        }

    cout<<dfs(1,1);
 
    return 0;
}

---

2.2189 数字三角形W

 时间限制: 1 s

 空间限制: 32000 KB

 题目等级 : 黄金 Gold

 

题目描述 Description

数字三角形
要求走到最后mod 100最大

输入描述 Input Description

第1行n，表示n行
第2到n+1行为每个的权值

输出描述 Output Description

mod 100最大值

样例输入 Sample Input

2
1
99 98

样例输出 Sample Output

99

数据范围及提示 Data Size & Hint

n<=25

思路:

　　1)暴力!悄悄地告诉你这道题其实将输入数据输进去之后,直接输出“99”,能拿到90~(数据醉了……)

　　2)DP

　　　　bool f[i][j][k]  表示从(1,1)到(i,j)的一条路径在mod p时的数字和若为k,true;否则,false.

　　　　转移方程:f[i][j][k] = f[i-1][j-1][k-s[i][j]] or  f[i-1][j][k-s[i][j]] .

　　　　注意!!!k-s[i][j]可能小于0,此时要+100;

　　　3)DFS

　　　　　没什么好说的其实……,就是普通的记忆化搜索

真代码酱来也~

//暴力
#include<iostream>
#define M 1111

using namespace std;

int n,f[M][M],sz[M][M];

int main()
{
    int i,j; 
    cin>>n;
    for(i=1;i<=n;i++)
        for(j=1;j<=i;j++)
            cin>>sz[i][j];
    if(n==5) cout<<"30";
    else cout<<"99";
    return 0;
}



//DP
#include<iostream>

using namespace std;

int n;
int s[26][26];
bool f[26][26][100];

int main()
{
  int maxx = 1<<31;
//读入数据
  cin>>n;
  for(int i=1; i<=n; i++)
    for(int j=1; j<=i; j++)
      cin>>s[i][j];
//DP(for)
  f[1][1][s[1][1]%100] = true;
  for(int i=2; i<=n; i++)
    for(int j=1; j<=i; j++)
      for(int k=1; k<=99; k++)
      {
        int temp = k-s[i][j];
        if(temp<0) temp+=100;
        f[i][j][k] = f[i-1][j-1][temp] | f[i-1][j][temp];
      }
//输出答案
  for(int j=1; j<=n; j++)
    for(int k=s[n][j]; k<=99; k++)
      if(f[n][j][k] && k>maxx) maxx = k;
        cout<<maxx<<endl;
  return 0;
}



//DP(DFS)
#include<iostream>

using namespace std;

int n,maxn;
int s[26][26];

void init()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>s[i][j];
}

void dfs(int x,int y,int nowsum)
{
    if(x>n||y>n) return; //maybe can 优化? 
    if(x==n)
    {
        if(maxn<nowsum%100) maxn=nowsum%100;
        return;
    }
    dfs(x+1,y,nowsum+s[x+1][y]);
    dfs(x+1,y+1,nowsum+s[x+1][y+1]);
}

int main()
{

    init(); //读入 
    dfs(1,1,s[1][1]);
    cout<<maxn%100<<endl;
    return 0;
}

---

3.2193 数字三角形WW

 时间限制: 1 s

 空间限制: 32000 KB

 题目等级 : 钻石 Diamond

 

题目描述 Description

数字三角形必须经过某一个点，使之走的路程和最大

输入描述 Input Description

第1行n，表示n行
第2到n+1行为每个的权值
程序必须经过n div 2,n div 2这个点//就是必须经过(n/2,n/2)这个点。

输出描述 Output Description

最大值

样例输入 Sample Input

2
1
1 1

样例输出 Sample Output

2

数据范围及提示 Data Size & Hint

n <=25

思路:

　　1)因为需要经过这个点,根据题意的话,那么这一行里的其他所有点都不能够被选上,所以将这一行的其他所有点的值赋值为一个较小的数,然后再进行像上面一样的操作就好啦~

　　2)其实还可以反过来想,将这个必须要做过的点手动加上一个较大的数值,然后再进行输出时在手动减去这个数值也是对的,而且我认为比上面的方法更加简单~

代码酱来也~

1)DP(记忆化DFS)

#include <iostream>
#include <cstdio>
#include <algorithm>
#define M 33

using namespace std;

int n;
int gg[M][M];
int v[M][M];

int dfs(int i,int j)
{
    if(v[i][j]==-1)
    {
        v[i][j]=gg[i][j]+max(dfs(i+1,j),dfs(i+1,j+1));
    }
    return v[i][j];
}

int main()
{
    scanf("%d",&n);
    int dx,dy;
    dx=dy=n/2;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
        {
            scanf("%d",&gg[i][j]);
            if(i == dx&&j != dy) gg[i][j]=-23333;//那重要的一步赋值
            if(i == n) v[i][j]=gg[i][j];
            else v[i][j]=-1;
        }

    cout<<dfs(1,1);

    return 0;
}

2)DP(for)

#include <iostream>
#define M 111

using namespace std;

int n,m[M][M];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>m[i][j];

    int dx,dy;
    dx=dy=n/2;
    m[dx][dy]+=1000000;//手动进行赋值操作
    for(int i=n-1;i>=1;i--)
        for(int j=1;j<=i;j++)//逆序! 
            m[i][j]+=max(m[i+1][j],m[i+1][j+1]);

    cout<<m[1][1]-1000000;//减回来

    return 0;
}

---

4.2198 数字三角形WWW

 时间限制: 1 s

 空间限制: 32000 KB

 题目等级 : 钻石 Diamond

 

题目描述 Description

数字三角形必须经过某一个点，使之走的路程和最大

输入描述 Input Description

第1行n，表示n行 
第2到n+1行为每个的权值
第n+2行为两个数x,y表示必须经过的点

输出描述 Output Description

最大值

样例输入 Sample Input

2
1
1 1
1 1

样例输出 Sample Output

2

数据范围及提示 Data Size & Hint

n<=25

思路:

　　上一个题的进化版!!!就是将固定的点换为给出的点,所以只需要在给出点后再进行赋值操作即可

代码酱来也~

1)DP(记忆化DFS)

#include <iostream>
#include <cstdio>
#include <algorithm>
#define M 33

using namespace std;

int n;
int gg[M][M];
int v[M][M];

int dfs(int i,int j)
{
    if(v[i][j]==-1)
    {
        v[i][j]=gg[i][j]+max(dfs(i+1,j),dfs(i+1,j+1));
    }
    return v[i][j];
}

int main()
{
    scanf("%d",&n);
    int dx,dy;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
        {
            scanf("%d",&gg[i][j]);
            if(i == n) v[i][j]=gg[i][j];
            else v[i][j]=-1;
        }
    scanf("%d%d",&dx,&dy);
    for(int i=1;i<=n;i++)
    {
        if(dx == n&&i != dy)//特判如果是最后一行 
        {
            gg[dx][i]=-233333;
            v[dx][i]=-233333;//将最后一行已经赋好值的v数组数值重新赋值为一个极小值 
        }
        else if(dx != n&&i != dy)//如果不是最后一行 
        {
            gg[dx][i]=-233333;//仅仅只将用到的gg数组 
        }
    }

    cout<<dfs(1,1);

    return 0;
}

2)DP(for)

#include <iostream>
#define M 111

using namespace std;

int n,m[M][M];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=i;j++)
            cin>>m[i][j];

    int dx,dy;
    cin>>dx>>dy;
    m[dx][dy]+=1000000;
    for(int i=n-1;i>=1;i--)
        for(int j=1;j<=i;j++)//逆序! 
            m[i][j]+=max(m[i+1][j],m[i+1][j+1]);

    cout<<m[1][1]-1000000;

    return 0;
}

---

 5.过河卒(洛谷P1002 codevs 1010)

2002年NOIP全国联赛普及组

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

　如图，A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。

同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。

例如上图 C 点上的马可以控制 9 个点（图中的P1，P2 … P8 和 C）。卒不能通过对方马的控制点。

　　棋盘用坐标表示，A 点（0，0）、B 点（n,m）(n,m 为不超过 20 的整数，并由键盘输入)，

同样马的位置坐标是需要给出的（约定: C不等于A，同时C不等于B）。

现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。

1<=n,m<=15

输入描述 Input Description

　键盘输入
　　　B点的坐标（n,m）以及对方马的坐标（X,Y）{不用判错}

输出描述 Output Description

　　屏幕输出
　　　　一个整数（路径的条数）。

样例输入 Sample Input

　6 6 3 2

样例输出 Sample Output

17

坑点:

　　由题目能够看出,n是列数,m是行数!这个绝对不能够搞反……我调了好长时间就因为这个!读题需谨慎! 

思路:

　　1)因为马所在点和马能够一步跳跃的点是不可以走的,所以要先开个数组标记一下

　　2)因为给出的图坐标是从0开始进行的,然而如果0-1将会成为负数,所以需要手动坐标进行+1操作

　　3)因为卒只能往右或下跳,所以每个点都是由它上边的点或左边的点扩展来的,然后我们运用类似前缀和的做法,每个ssr数组上记录的是到达此点的路径条数，所以最后一个点(终点)上记录的就是从A到B的所有路径

代码酱来也~

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

const int M = 2333;

int n,m;
int mx,my;
long long ssr[M][M];
bool v[M][M];
const int dx[9]={0,-2,-1,1,2,-2, 1,-1, 2},//m
          dy[9]={0, 1, 2,2,1,-1,-2,-2,-1};//n

int main()
{
    scanf("%d%d%d%d",&n,&m,&mx,&my);
//    因为题目中说的时候给出的是(n,m)坐标,所以n是列数,m是行数 
    for(int i=0;i<=8;i++)
    {
        int nx=mx+dx[i],ny=my+dy[i];
        if(nx>m||nx<0||ny>n||ny<0) continue;
        v[nx+1][ny+1]=1;//不能通过 
    }

    ssr[1][1]=1;
    for(int i=1;i<=n+1;i++)
    for(int j=1;j<=m+1;j++)
    {
        if(!v[i][j])
        {
            ssr[i][j]+=ssr[i-1][j]+ssr[i][j-1];
        }
    }

    cout<<ssr[n+1][m+1];

    return 0;
}

---

6.装箱问题(洛谷 P1049 codevs 1014)

2001年NOIP全国联赛普及组

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

有一个箱子容量为V（正整数，0＜＝V＜＝20000），同时有n个物品（0＜n＜＝30），每个物品有一个体积（正整数）。

要求n个物品中，任取若干个装入箱内，使箱子的剩余空间为最小。

输入描述 Input Description

一个整数v，表示箱子容量

一个整数n，表示有n个物品

接下来n个整数，分别表示这n 个物品的各自体积

输出描述 Output Description

一个整数，表示箱子剩余空间。

样例输入 Sample Input

24

6

8

3

12

7

9

7

样例输出 Sample Output

0

思路:

　　f数组里记录的是最大能够存放的物体的体积,我们在输入的时候可以将每个物体的先在c数组中记录一下,然后用01背包思想做一下就行(跟01背包问题有些神似~)

　　所以对于每件物品我们有不放和放两种情况(转移方程:　　f[j] = max(f[j],f[j-vi[i]]+c[i]);)

代码酱来也~

#include <iostream>
#include <cstdio>
#include <algorithm>
#define M 23333

using namespace std;

int v,n;
//v 20000 n 30
long long vi[M];//每个物品的体积 
long long f[M];//存放的是背包里面盛放的东西的体积和 
long long c[M];//相当于以前做的01背包中的价值 

int main()
{
    scanf("%d",&v);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        cin>>vi[i];
        c[i]=vi[i];
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=v;j>=vi[i];j--)//最低不能小于i的体积
        {
            f[j]=max(f[j],f[j-vi[i]]+c[i]);
        }
    }

    cout<<v-f[v];

    return 0;
}

---

7.方格取数(洛谷 P1001 codevs 1043)

2000年NOIP全国联赛提高组

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

设有N*N的方格图(N<=10,我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0。如下图所示（见样例）：

某人从图的左上角的A 点出发，可以向下行走，也可以向右走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从A点到B 点共走两次，试找出2条这样的路径，使得取得的数之和为最大。

 

输入描述 Input Description

输入的第一行为一个整数N（表示N*N的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的0表示输入结束。

输出描述 Output Description

    只需输出一个整数，表示2条路径上取得的最大的和。

样例输入 Sample Input

      8

      2  3  13

      2  6   6

      3  5   7

      4  4  14

      5  2  21

      5  6   4

      6 3  15

      7 2  14

      0 0  0

样例输出 Sample Output

      67

数据范围及提示 Data Size & Hint

如描述

思路:

　　在注释里w

代码酱来也~

#include<iostream>
#include<cstdio>

using namespace std;

const int N = 10;

int n,x,y,sum[N][N];
int num[N][N],f[N][N][N][N];

int main()
{
    scanf("%d",&n);
    while(scanf("%d%d",&x,&y) == 2)//进行输入的方式 
    {
        if(!x) break;//结束条件 
        cin>>sum[x][y];
    }

    for(int i=1; i<=n; i++)
    for(int j=1; j<=n; j++)
    for(int l=1; l<=n; l++)
    for(int k=1; k<=n; k++)
    {
        if(i+j!=l+k) continue;//如果没有同时进行,不进行接下来的操作 
//        f[i][j][k][l]第一条路径走到(i,j)时,第二条路径走到(k,l)的最优解
        f[i][j][l][k] = max(f[i][j][l][k],f[i-1][j][l-1][k]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i][j-1][l][k-1]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i-1][j][l][k-1]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i][j-1][l-1][k]);
        f[i][j][l][k]+= sum[i][j]+sum[l][k];//现在取得的数,就是他们两个分别取得数的和 
        if(i==l&&j==k) f[i][j][l][k]-=sum[l][k];//-=sum[i][j]; 
//        如果都是到达的一个终点,那么最后的终点格子上的数只能取得一次 
    }

    cout<<f[n][n][n][n]<<endl;//从起点到同一终点(n,n)所取最大数 

    return 0;
}

---

8.合唱队形(洛谷 P1091 codevs 1058)

2004年NOIP全国联赛提高组

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

    N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。

    合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1，2…，K，他们的身高分别为T1，T2，…，TK，  则他们的身高满足T1<...<Ti>Ti+1>…>TK(1<=i<=K)。

    你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入描述 Input Description

    输入文件chorus.in的第一行是一个整数N(2<=N<=100)，表示同学的总数。第一行有n个整数，用空格分隔，第i个整数Ti(130<=Ti<=230)是第i位同学的身高(厘米)。

输出描述 Output Description

    输出文件chorus.out包括一行，这一行只包含一个整数，就是最少需要几位同学出列。

样例输入 Sample Input

8
186 186 150 200 160 130 197 220

样例输出 Sample Output

4

数据范围及提示 Data Size & Hint

对于50％的数据，保证有n<=20；
对于全部的数据，保证有n<=100。

思路:

　　

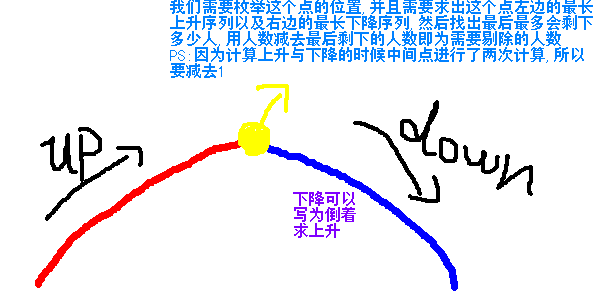
代码酱来也~

#include <iostream>
#include <cstdio>
#include <algorithm>
#define M 23333

using namespace std;

int n,ans;
int t[M];//存放身高 
int f[M];//正着寻找上升子序列  
int g[M];//倒着寻找上升子序列(就是正着寻找下降子序列) 

void shangsheng()
{
    f[1]=1;
    for(int i=2;i<=n;i++)//从第二个点开始寻找,因为第一个点的上升子序列一定为1(前面没有数) 
    {
        for(int j=1;j<=i-1;j++)//通过前面已经找好了的序列更新当前序列 
            if(t[i]>t[j]&&f[i]<f[j])//求上升子序列 
                f[i]=f[j];
        f[i]++;
//        表示如果没有进行更新的话,他自己就是一个点,所以进行++
//(其实就是相当于在一开始的时候进行初始化为1,可以将其去掉然后加个初始化)        
    }

}

void xiajiang()//同理(只是将顺序反过来) 
{
    g[n]=1;
    for(int i=n-1;i>=1;i--)
    {
        for(int j=i+1;j<=n;j++)
            if(t[i]>t[j]&&g[i]<g[j])
                g[i]=g[j];
        g[i]++;        
    }

}

void DP()
{
    for(int i=1;i<=n;i++)
        ans=max(ans,f[i]+g[i]-1);
//        因为最中间的那一个人被计算了2次,所以减去他自己 
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&t[i]);
    }

    shangsheng();
    xiajiang();
    DP();

    printf("%d\n",n-ans);
//    因为ans纪录的是最多剩下多少个人能够组成合唱队形,然而输出的是剔除多少人 

    return 0;
}

---

9.codevs 1048 石子归并

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

有n堆石子排成一列，每堆石子有一个重量w[i], 每次合并可以合并相邻的两堆石子，一次合并的代价为两堆石子的重量和w[i]+w[i+1]。问安排怎样的合并顺序，能够使得总合并代价达到最小。

输入描述 Input Description

第一行一个整数n（n<=100）

第二行n个整数w1,w2...wn  (wi <= 100)

输出描述 Output Description

一个整数表示最小合并代价

样例输入 Sample Input

4

4 1 1 4

样例输出 Sample Output

18

思路:

　　1)你可以倒序枚举左端点从n-1到1,(因为左端点右边还有右端点,不能为n,所以从n-1开始枚举),然后用r枚举右端点最起码是l+1(至少为左端点的右边一个)

　　　　　　　　可以结合01背包来进行考虑

　　2)先求出所有长度为2的区间,再求出所有长度为3的区间...最后求出长度为n的区间

　　　　　　　　因为小区间都是求过的,可以直接使用

　　3)先求出区间右端点是2的区间,再求出区间右端点是3的区间...求出区间右端点是n的区间

　　　　　　　　在求解以r为区间右端点的区间时,区间右端点小于r的区间都可以直接使用.

　　　　　　　　如果求区间[l,r],那么要用到区间[l,k]和[k+1,r],其中[l,k]可以直接使用,

　　　　　　　　而要使用[k+1,r]就必须在求解[l,r]之前先求解[k+1,r],

　　　　　　　　又因为k+1>l,所以在求解区间右端点为j的区间时,左端点要从右向左枚举

代码酱来也~

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define M 233

using namespace std;

int n;
int wi[M];//重量 
int sum[M];//前缀和计算 
int f[M][M];//进行输出,里面存放的是l到r所得到的最小积分

int max(int a, int b)
{return a > b ? a : b;}
int min(int a, int b)
{return a < b ? a : b;}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&wi[i]);
        sum[i]+=sum[i-1]+wi[i];    //计算前缀和 
    }

    memset(f,0x3f,sizeof(f));//初始化
//    这里的0x3f不能够改为0x7f,会爆出负数... 
    for(int i=1;i<=n;i++)
    {
        f[i][i]=0;//自己跟自己合并不需要能量
    }

/* 寻找左端点是l的,一直到最后n(不同区间长度)所使用的最少价值 */
//    for(int l=n-1;l>=1;l--) 
//        for(int r=l+1;r<=n;r++)

/* 先求出区间右端点是2的区间,再求出区间右端点时3的区间...最后求出区间右端点是n的区间 */ 
//    for(int r=1;r<=n;r++)
//        for(int l=r-1;l;l--)

/* 先求出所有长度为2的区间,再求出所有长度为3的区间...最后求出长度为n的区间 */
    for(int d=2;d<=n;d++)//区间长度 
        for(int l=1;l<=n-d+1;l++)//左边端点,因为区间长度为d,所以左边端点最大就是堆数减去区间长度+1,可以仔细想一下 
        {//因为区间长度是对于线段来说,而端点却是点,所以需要进行 +1 -1 啊什么的 
            int r=l+d-1;//右端点就是左端点+区间长度-1 
//            如果用上面2种方法的话上面一句不用加 
            for(int k=1;k<r;k++)
            {
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+sum[r]-sum[l-1]);
            }
        }

    cout<<f[1][n]<<endl;

    return 0;
}

---

10.传纸条 codevs 1169 洛谷P1006

2008年NOIP全国联赛提高组

 时间限制: 1 s

 空间限制: 128000 KB

 

题目描述 Description

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个m行n列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用0表示），可以用一个0-100的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度只和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入描述 Input Description

输入的第一行有2个用空格隔开的整数m和n，表示班里有m行n列（1<=m,n<=50）。

接下来的m行是一个m*n的矩阵，矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度。每行的n个整数之间用空格隔开。

输出描述 Output Description

输出共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

样例输入 Sample Input

3 3

0 3 9

2 8 5

5 7 0

样例输出 Sample Output

34

数据范围及提示 Data Size & Hint

30%的数据满足：1<=m,n<=10

100%的数据满足：1<=m,n<=50

 思路:

　　　可以转化为方格取数问题~

代码酱来也~

#include<iostream>
#include<cstdio>

using namespace std;

const int N = 51;

int m,n,x,y,sum[N][N];
int num[N][N],f[N][N][N][N];

int main()
{
    /* 可以手动转化为方格取数问题 */
    scanf("%d%d",&m,&n);
    for(int i=1;i<=m;i++)//修改一下输入方式 
        for(int j=1;j<=n;j++)
            scanf("%d",&sum[i][j]);

    for(int i=1; i<=m; i++)
    for(int j=1; j<=n; j++)
    for(int l=1; l<=m; l++)
    for(int k=1; k<=n; k++)
    {
        if(i+j!=l+k) continue;//如果没有同时进行,不进行接下来的操作 
//        f[i][j][k][l]第一条路径走到(i,j)时,第二条路径走到(k,l)的最优解
        f[i][j][l][k] = max(f[i][j][l][k],f[i-1][j][l-1][k]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i][j-1][l][k-1]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i-1][j][l][k-1]);
        f[i][j][l][k] = max(f[i][j][l][k],f[i][j-1][l-1][k]);
        f[i][j][l][k]+= sum[i][j]+sum[l][k];//现在取得的数,就是他们两个分别取得数的和 
        if(i==l&&j==k) f[i][j][l][k]-=sum[l][k];//-=sum[i][j]; 
//        如果都是到达的一个终点,那么最后的终点格子上的数只能取得一次 
    }

    cout<<f[m][n][m][n]<<endl;//从起点到同一终点(m,n)所取最大数 

    return 0;
}

---

11.洛谷 P2639[USACO09OCT]Bessie的体重问题Bessie's We…

题目描述

Bessie像她的诸多姊妹一样，因为从Farmer John的草地吃了太多美味的草而长出了太多的赘肉。所以FJ将她置于一个及其严格的节食计划之中。她每天不能吃多过H (5 <= H <= 45,000)公斤的干草。 Bessie只能吃一整捆干草；当她开始吃一捆干草的之后就再也停不下来了。她有一个完整的N (1 <= N <= 500)捆可以给她当作晚餐的干草的清单。她自然想要尽量吃到更多的干草。很自然地，每捆干草只能被吃一次（即使在列表中相同的重量可能出现2次，但是这表示的是两捆干草，其中每捆干草最多只能被吃掉一次）。 给定一个列表表示每捆干草的重量S_i (1 <= S_i <= H), 求Bessie不超过节食的限制的前提下可以吃掉多少干草（注意一旦她开始吃一捆干草就会把那一捆干草全部吃完）。

输入输出格式

输入格式：

• 第一行: 两个由空格隔开的整数: H 和 N * 第2到第N+1行: 第i+1行是一个单独的整数，表示第i捆干草的重量S_i。

输出格式：

• 第一行: 一个单独的整数表示Bessie在限制范围内最多可以吃多少公斤的干草。

输入输出样例

输入样例#1：

56 4
15
19
20
21

输出样例#1：

56

说明

输入说明:

有四捆草，重量分别是15, 19, 20和21。Bessie在56公斤的限制范围内想要吃多少就可以吃多少。

输出说明:

Bessie可以吃3捆干草（重量分别为15, 20, 21）。恰好达到她的56公斤的限制。

思路:

　　虽然这道题有说到同一种公斤的干草只能够吃一次,但是这个并不能够影响我们用一维背包做题,因为如果要装入一捆干草的话,第一种情况是里面没有与他相同公斤数的干草直接加入,代入转移方程进行比较,而第二种情况则是里面拥有相同公斤数的干草,那么在运用转移方程的时候,需要将里面腾出当前公斤数的空间,就像大于是把相同公斤数量的干草腾出来了,所以不需要考虑同种干草是否是只吃了一次...好久没有想过来...

转移方程:

　　f[j]=max(f[j],f[j-v[i]]+c[i]);

代码酱来也~

#include <iostream>
#include <cstdio>
#define M 45233

using namespace std;

int m,n;
int v[M],c[M];
int f[M];

int main()
{
    scanf("%d%d",&m,&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&v[i]); 
        c[i]=v[i];
    }

    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+c[i]);
        }
    }

    printf("%d\n",f[m]);

    return 0;
}

---

12.洛谷 P1541 乌龟棋 codevs 1068 乌龟棋

题目背景

小明过生日的时候，爸爸送给他一副乌龟棋当作礼物。

题目描述

乌龟棋的棋盘是一行N个格子，每个格子上一个分数（非负整数）。棋盘第1格是唯一的起点，第N格是终点，游戏要求玩家控制一个乌龟棋子从起点出发走到终点。

乌龟棋中M张爬行卡片，分成4种不同的类型（M张卡片中不一定包含所有4种类型的卡片，见样例），每种类型的卡片上分别标有1、2、3、4四个数字之一，表示使用这种卡片后，乌龟棋子将向前爬行相应的格子数。游戏中，玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片，控制乌龟棋子前进相应的格子数，每张卡片只能使用一次。

游戏中，乌龟棋子自动获得起点格子的分数，并且在后续的爬行中每到达一个格子，就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。

很明显，用不同的爬行卡片使用顺序会使得最终游戏的得分不同，小明想要找到一种卡片使用顺序使得最终游戏得分最多。

现在，告诉你棋盘上每个格子的分数和所有的爬行卡片，你能告诉小明，他最多能得到多少分吗？

输入输出格式

输入格式：

输入文件的每行中两个数之间用一个空格隔开。

第1行2个正整数N和M，分别表示棋盘格子数和爬行卡片数。

第2行N个非负整数，a1a2……aN，其中ai表示棋盘第i个格子上的分数。

第3行M个整数，b1b2……bM，表示M张爬行卡片上的数字。

输入数据保证到达终点时刚好用光M张爬行卡片。

输出格式：

输出只有1行，1个整数，表示小明最多能得到的分数。

输入输出样例

输入样例#1：

9 5
6 10 14 2 8 8 18 5 17
1 3 1 2 1

输出样例#1：

73

说明

每个测试点1s

小明使用爬行卡片顺序为1，1，3，1，2，得到的分数为6+10+14+8+18+17=73。注意，由于起点是1，所以自动获得第1格的分数6。

对于30%的数据有1≤N≤30，1≤M≤12。

对于50%的数据有1≤N≤120，1≤M≤50，且4种爬行卡片，每种卡片的张数不会超过20。

对于100%的数据有1≤N≤350，1≤M≤120，且4种爬行卡片，每种卡片的张数不会超过40；0≤ai≤100，1≤i≤N；1≤bi≤4，1≤i≤M。

思路:

　　这道题让我情不自禁的想到传纸条那题呢!

　　没错!我们就是用四维dp来做!

代码酱来也~

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int Qi[521];
int num[5];
int dp[51][51][51][51];
int n,m;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&Qi[i]);
    int v;
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&v);
        num[v]++;
    }
    dp[0][0][0][0]=Qi[1];
    for(int i=0;i<=num[1];i++)
    for(int j=0;j<=num[2];j++)
    for(int k=0;k<=num[3];k++)
    for(int w=0;w<=num[4];w++)
    {
//        if(i==0 && j==0 && k==0 && w==0) continue;
        int maxx=0;
        if(i) maxx=max(dp[i-1][j][k][w],maxx);
        if(j) maxx=max(dp[i][j-1][k][w],maxx);
        if(k) maxx=max(dp[i][j][k-1][w],maxx);
        if(w) maxx=max(dp[i][j][k][w-1],maxx);
        dp[i][j][k][w]=maxx+Qi[1+i+j*2+k*3+w*4];
    }
    printf("%d",dp[num[1]][num[2]][num[3]][num[4]]);
    return 0;
}

---

13.1267 老鼠的旅行

2012年CCC加拿大高中生信息学奥赛

 时间限制: 1 s

 空间限制: 128000 KB

 题目等级 : 黄金 Gold

 

题目描述 Description

You are a mouse that lives in a cage in a large laboratory.

你是一只生活在笼子里的实验室老鼠。

The laboratory is composed of one rectangular grid of square cages, with a total of R rows and C columns of cages (1 ≤ R,C ≤ 25).

实验室是一个R行C列的格子矩阵(1 ≤ R,C ≤ 25). 每个格子是一个笼子. (尼玛还要我活么……)

To get your exercise, the laboratory owners allow you to move between cages.

为了让你锻炼身体，实验室管理员允许你在笼子之间移动。

You can move between cages either by moving right between two adjacent cages in the same row, or by moving down between two adjacent cages in the same column.

你只能向右和向下移动。

You cannot move diagonally, left or up.

你不能斜着移动，也不能向上和向左移动。

Your cage is in one corner of the laboratory, which has the label (1,1) (to indicate top-most row, left-most column).

你所在的笼子是实验室的左上角，标记为(1,1)

You would like to visit your brother who lives in the cage labelled (R,C) (bottom-most row, right-most column), which is in the other corner diagonally.

你想去右下角的笼子(R,C)里找你的女朋友(尼玛老鼠也有女盆友么！！！)

However, there are some cages which you cannot pass through, since they contain cats.

但是有一些笼子是不能经过的，因为里面有猫（谁说老鼠怕猫么，还有，管理员有毛病么……）

Your brother, who loves numbers, would like to know how many different paths there are between your cage and his that do not pass through any cat cage. Write a program to compute this number of cat-free paths.

你女朋友很爱数学，她想要知道有多少条不同的路径可以从你的笼子到达她的笼子。写一个程序来计算吧。（这样的女朋友不要也罢……）

输入描述 Input Description

The first line of input contains two integers R and C, separated by one space representing the number of rows and columns (respectively). On the second line of input is the integer K, the number of cages that contain cats. The next K lines each contain the row and column positions (in that order) for a cage that contains a cat. None of the K cat cages are repeated, and all cages are valid positions. Note also that (1,1) and (R,C) will not be cat cages.

第一行包含2个整数R和C，第二行一个整数K，代表包含猫的笼子的个数，接下来K行包含K个不同的位置信息，代表K个包含猫的笼子的位置信息，注意(1,1)和(R,C)这两个位置是不会有猫的， 否则出题者就没法活了……

输出描述 Output Description

Output the non-negative integer value representing the number of paths between your cage at position (1,1) and your brother’s cage at position (R,C). You can assume the output will be strictly less than 1 000 000 000.

输出一个非负整数代表你可以去你女朋友笼子里和她啪啪啪的路径数目，你可以假设这个输出会严格小于1,000,000,000。

样例输入 Sample Input

样例输入 1:

2 3

1

2 1

样例输入 2:

3 4

3

2 3

2 1

1 4

样例输出 Sample Output

样例输出 1: 2

样例输出 2: 1

 思路:(神TM翻译....)

　　因为只能向右向下行走,所以dp转移方程是

　　　　　　　　　　　　　　　　　　dp[i][j]=dp[i-1][j]+dp[i][j-1];

　　　　　　　　　　　　　　　　　　或dp[i][j]=dp[i-1][j];

　　　　　　　　　　　　　　　　　　或dp[i][j]=dp[i][j-1];

 　　因为有的地方是不能够走的.所以需要加上特判:

　　　　　　　　　　　　　　　　　　if(!Ls[i][j]) (Ls数组里面存放的是是否有老鼠).

坑点:

　　你需要进行初始化,初始化如果为dp[0][1]=1,或者是dp[1][0]=1的时候,不需要加特判i与j是否在第一行或第一列,直接使用第一个转移方程即可,但是如果初始化的是dp[1][1]=1;你就需要在第二个for循环里加上特判,i与j的值

代码:

#include <iostream>
#include <cstdio>

using namespace std;

const int Mod = 1e9;
const int M = 33;
int n,m,k;///行,列
int dp[M][M],Ls[M][M]; 

int main()
{
    scanf("%d%d",&n,&m);
    scanf("%d",&k);
    for(int i=1,x,y;i<=k;i++)
    {
        scanf("%d%d",&x,&y);
        Ls[x][y]=1;
    }
    dp[1][1]=1; 
//    dp[1][0]=1;
//    dp[0][1]=1; 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(Ls[i][j]==0)
            {
                if(i>1 && j>1)
                    dp[i][j]=dp[i-1][j]%Mod+dp[i][j-1]%Mod,dp[i][j]%=Mod;
                if(i==1 && j!=1)
                    dp[i][j]=dp[i][j-1]%Mod;
                if(j==1 && i!=1)
                    dp[i][j]=dp[i-1][j]%Mod; 
            }
        }
    }
    printf("%d",dp[n][m]);
    return 0;
}

---

14.luoguP1057 传球游戏

题目描述

上体育课的时候，小蛮的老师经常带着同学们一起做游戏。这次，老师带着同学们一起做传球游戏。

游戏规则是这样的：n个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师在此吹哨子时，传球停止，此时，拿着球没有传出去的那个同学就是败者，要给大家表演一个节目。

聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了m次以后，又回到小蛮手里。两种传球方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有三个同学1号、2号、3号，并假设小蛮为1号，球传了3次回到小蛮手里的方式有1->2->3->1和1->3->2->1，共2种。

输入输出格式

输入格式：

输入文件ball.in共一行，有两个用空格隔开的整数n，m（3<=n<=30，1<=m<=30）。

输出格式：

输出文件ball.out共一行，有一个整数，表示符合题意的方法数。

输入输出样例

输入样例#1：

3 3

输出样例#1：

2

说明

40%的数据满足：3<=n<=30，1<=m<=20

100%的数据满足：3<=n<=30，1<=m<=30

2008普及组第三题

思路:

　　题目里面其实说的很明白啦:

　　　　　　每个同学可以把球传给自己左右的两个同学中的一个（左右任意）

　　那么dp转移方程就粗来啦~

　　dp[i][j]=dp[i-1][j-1]+dp[i+1][j-1];

坑点:

　　因为题目中提到:

　　　　　　n个同学站成一个圆圈 

　　故我们的第一个人和最后一个人就很不好受啦~（因为（n+1）>n，（1-1）<1，没这俩人嘻嘻）

　　所以需要加个特判~

上代码:

#include <iostream>
#include <cstdio>
using namespace std;

const int N = 31;
const int M = 31;
int n,m;
//dp[i][j]表示从i开始传j次又传到i的次数 
int dp[N][M];

int main()
{
    scanf("%d%d",&n,&m);
    //一开始如果不传的话就只有一种情况:
    //自己拿着 
    dp[1][0]=1;
    for(int j=1;j<=m;j++)
    {
        for(int i=1;i<=n;i++)
        {
            if(i==1)
                dp[i][j]=dp[i+1][j-1]+dp[n][j-1];
            else
                if(i==n)
                    dp[i][j]=dp[i-1][j-1]+dp[1][j-1];
            else 
                dp[i][j]=dp[i-1][j-1]+dp[i+1][j-1];
        }
    }
    printf("%d",dp[1][m]);
    return 0;
}

End.