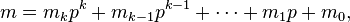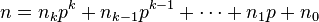数论——Lucas定理模板

Formulation

For non-negative integers m and n and a prime p, the following congruence relation holds:

\binom{m}{n}\equiv\prod_{i=0}^k\binom{m_i}{n_i}\pmod p,

where

m=m_kp^k+m_{k-1}p^{k-1}+\cdots +m_1p+m_0,

and

n=n_kp^k+n_{k-1}p^{k-1}+\cdots +n_1p+n_0

are the base p expansions of m and n respectively.

 

#include <iostream>
#include <cstdio>
#include <cstring>
usingnamespace std;

typedef longlong llg;

constint N =150000;

llg n, m, p, fac[N];

void init()
{
    int i;
    fac[0] =1;
    for(i =1; i <= p; i++)
        fac[i] = fac[i-1]*i % p;
}

llg pow(llg a, llg b)
{
    llg tmp = a % p, ans =1;
    while(b)
    {
        if(b &1)  ans = ans * tmp % p;
        tmp = tmp*tmp % p;
        b >>=1;
    }
    return  ans;
}

llg C(llg n, llg m)
{
    if(m > n)  return0;
    return  fac[n]*pow(fac[m]*fac[n-m], p-2) % p;
}

llg Lucas(llg n, llg m)
{
    if(m ==0)  return1;
    elsereturn  (C(n%p, m%p)*Lucas(n/p, m/p))%p;
}

int main()
{
    int t;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%I64d%I64d%I64d", &n, &m, &p);
        init();
        printf("%I64d\n", Lucas(n+m, n));
    }
    return0;
}

　　

posted on 2011-09-17 13:42  Moon_1st  阅读(3557)  评论(0)  编辑  收藏  举报

导航