HDU 1506 Largest Rectangle in a Histogram(单调栈)
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 20760 Accepted Submission(s):
6325
Problem Description
A histogram is a polygon composed of a sequence of
rectangles aligned at a common base line. The rectangles have equal widths but
may have different heights. For example, the figure on the left shows the
histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3,
measured in units where 1 is the width of the rectangles:
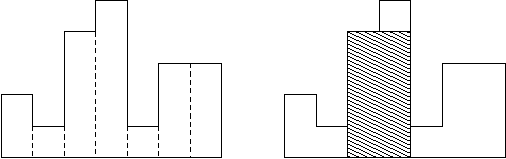
Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.
Input
The input contains several test cases. Each test case
describes a histogram and starts with an integer n, denoting the number of
rectangles it is composed of. You may assume that 1 <= n <= 100000. Then
follow n integers h1, ..., hn, where 0 <= hi <= 1000000000. These numbers
denote the heights of the rectangles of the histogram in left-to-right order.
The width of each rectangle is 1. A zero follows the input for the last test
case.
Output
For each test case output on a single line the area of
the largest rectangle in the specified histogram. Remember that this rectangle
must be aligned at the common base line.
Sample Input
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
Sample Output
8
4000
Source
Recommend
一道挺裸的单调栈
我们预处理出每一个位置向左/向右第一个比他小的位置
然后统计答案,这样很显然是对的
时间复杂度
#include<cstdio> #define LL long long #define max(a,b) (a>b?a:b) #define min(a,b) (a<b?a:b) using namespace std; const int MAXN = 100001; LL a[MAXN]; int s[MAXN], top = 0; int L[MAXN], R[MAXN]; void clear() {top = 0;} int main() { //#ifdef WIN32 //freopen("a.in", "r", stdin); //#endif int N; while(~scanf("%d", &N) && N != 0) { clear(); s[0] = 0; for(int i = 1; i <= N; i++) scanf("%I64d",&a[i]); for(int i = 1; i <= N; i++) { while(top > 0 && a[i] <= a[ s[top] ]) top--; L[i] = min(s[top] + 1, i); s[++top] = i; } clear(); s[0] = N + 1; for(int i = N; i >= 1; i--) { while(top > 0 && a[i] <= a[ s[top] ]) top--; R[i] = max(s[top] - 1, i); s[++top] = i; } LL Ans = 0; for(int i = 1; i <= N; i++) Ans = max(Ans, (R[i] - L[i] + 1) * a[i] ); printf("%I64d\n",Ans); } return 0; }
作者:自为风月马前卒
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 托管堆内存泄露/CPU异常的常见思路
· PostgreSQL 和 SQL Server 在统计信息维护中的关键差异
· C++代码改造为UTF-8编码问题的总结
· DeepSeek 解答了困扰我五年的技术问题
· 为什么说在企业级应用开发中,后端往往是效率杀手?
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· Trae初体验
2017-04-27 2973 枪毙
2017-04-27 2840 WIKIOI——评测
2017-04-27 1512 转向游戏
2017-04-27 1341 与3和5无关的数
2017-04-27 2843 拯救炜哥
2017-04-27 1001 舒适的路线 2006年
2017-04-27 1226 倒水问题