【codeforces 870F】Paths

Description

You are given a positive integer n. Let's build a graph on vertices 1, 2, ..., n in such a way that there is an edge between vertices u and v if and only if gcd(u,v)≠1. Let d(u, v) be the shortest distance between u and v, or 0 if there is no path between them. Compute the sum of values d(u, v) over all 1 ≤ u < v ≤ n.The gcd (greatest common divisor) of two positive integers is the maximum positive integer that divides both of the integers.

Input

Single integer n (1 ≤ n ≤ 107).

Output

Print the sum of d(u, v) over all 1 ≤ u < v ≤ n.

Examples

input

6

output

8

input

10

output

44

Note

All shortest paths in the first example: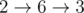

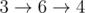
There are no paths between other pairs of vertices.The total distance is 2 + 1 + 1 + 2 + 1 + 1 = 8. 

题意：

给定数字n，建立一个无向图。对于所有1~n之间的数字，当数字gcd(u,v)≠1时将u、v连一条边，边权为1。d(u, v)表示u到v的最短路，求所有d(u, v)的和，其中1 ≤ u < v ≤ n。

 

分析：

对于1以及所有大于n/2的的质数，与其他数字均不联通，直接剔除。

对于剩下的数字：

1.当gcd(u,v)≠1时，d(u, v)==1。即对于数字u，小于u且d(u, v)==1的数字个数为x - 1 - φ(x)。

2.令p[u]表示数字u的最小质因子，则当p[u]·p[v] ≤ n时，d(u, v)==2。维护数组num、sum，num[i]代表最小质因子为i的数字个数，sum数组为num数组的前缀和。统计Σnum[i]·sum[n/i]可以覆盖所有p[u]·p[v] ≤ n的情况，其中减去自身与自身被统计的情况，剩下的所有数对都被统计了两次，其中包含gcd(u,v)≠1的情况，需进行相应处理，详见代码。

3.剩下的数对最短路一定为3，因为 u→2·p[u]→2·p[v]→v这条路一定存在。可通过数对总数减去d(u, v)==1与d(u, v)==2的情况得到。

 

#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
using namespace std;
const int N=1e7+5;
int n,m,tot,now,pri[N],p[N],phi[N],num[N],sum[N]; 
LL one,two,three;
int main()
{
    scanf("%d",&n);
    phi[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!p[i]){p[i]=pri[++tot]=i;phi[i]=i-1;}
        for(int j=1;j<=tot;j++)
        {
            if(i*pri[j]>n)break;
            p[i*pri[j]]=pri[j];
            if(i%pri[j]==0){phi[i*pri[j]]=phi[i]*pri[j];break;}
            else phi[i*pri[j]]=phi[i]*(pri[j]-1);
        }
    } 
    for(int i=2;i<=n;i++)one+=i-1-phi[i];
    for(int i=2;i<=n;i++)num[p[i]]++;
    for(int i=2;i<=n;i++)sum[i]=sum[i-1]+num[i];
    for(int i=2;i<=n;i++)two+=1ll*num[i]*sum[n/i];
    for(int i=2;i<=n;i++)if(1ll*p[i]*p[i]<=n)two--;
    two=two/2-one;m=n-1;
    for(int i=tot;i>=1;i--)
        if(pri[i]*2>n)m--;
        else break;
    three=1ll*m*(m-1)/2-one-two;
    printf("%I64d\n",one+two*2+three*3);
    return 0;
}