总结:代码实现过程
讲解下代码实现得整体思路,主要讲解一下我在降低时间复杂度的做出的思考,最后固态盘 win32 release 跑大概27.2s。
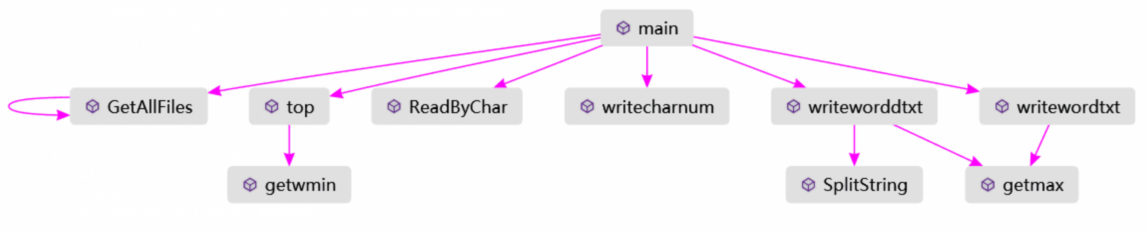
(函数调用图)
main调用GetALLFiles获取文件夹下所有文件名,进而传递给ReadByChar,统计字符,行数,单词,词组进map中储存起来,进而传递给top查找频率前十的单词与词组,进而调用writeworddtxt与writeword进行结果的输出。
首先是选择储存结构,不难想象170M左右的测试文件,统计字母,单词词组,首先就是想到的利用键值对,而且必然有大量的的查找,插入过程,这将是系统时间开销的主要部分,根据问题特性不难想到利用哈希表这一数据结构,将字符串hash作为键值,大大降低时间复杂度。并且c++11封装了无序关联容器unordered_map可以说十分方便,注意不要用普通map,因为普通map是基于红黑树的,查找开销较大。
unordered_map<string, int> word; //单词 数目 unordered_map<string, bitset<128>> wordd;//单词 对应应该大写的位 unordered_map<string, int> phrase; //词组 数目 unordered_map<string, string> wordend; //词 可能有的单词后缀
这便是我用于储存数据的四个unordered_map,为什么需要四个这么多呢?
首先我们看单词的类数,其实本质上分成两种,数字后缀的与不是数字后缀的,像kkkk12,Kkkk1233,非数字后缀的kkkk,kkkk123ad,Kkkk。
首先最简单的kkkk,我们直接往word里面存,但是之后遇到Kkkk呢?这时候Kkkk应该把kkkk覆盖并且单词数目+1,但是我根本不知道之前有没有kkkk或者KKkk之类的,那么我就想到加一个map用wordd中一个bitset对应位为1就代表word中string中当今字典顺序最靠前的哪一位是大写,比如只有kkkk,则在wordd中就有<kkkk,0000.....>,遇到Kkkk就变成<kkkk,1000.....>,最后输出时候再将对应位大写,代码中wordtostr完成这个任务。
但是还有kkkk123这种情况,我便又建立wordend来描述后缀,我们会把kkkk123与之前存的单词进行字典顺序比较,将靠前得存下来,word中以小写string为键,wordd中放对应的大写位,wordend放可能存在的数字后缀。
至于phrase就是储存词组的,在写好单词判定逻辑后,我加了几行代码就实现了功能,因此主要心血还是在单词判定上。下面就对这一步的逻辑进行阐述。
首先,对于读到的字符就下面三种情况,我们用flag代表可能要存入map的单词的长度,bitset<128>代表的可能的大写位数,num代表可能的数字后缀,sword代表可能写入的map的单词,sphrase存储上次成功储存的单词。
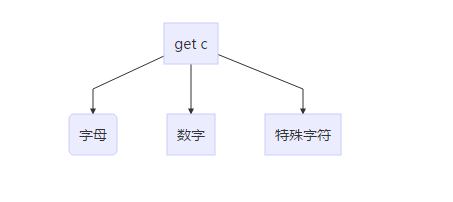
首先读到字母,读到字母逻辑最简单,因为这时候不存在可能的单词丢弃的情况。
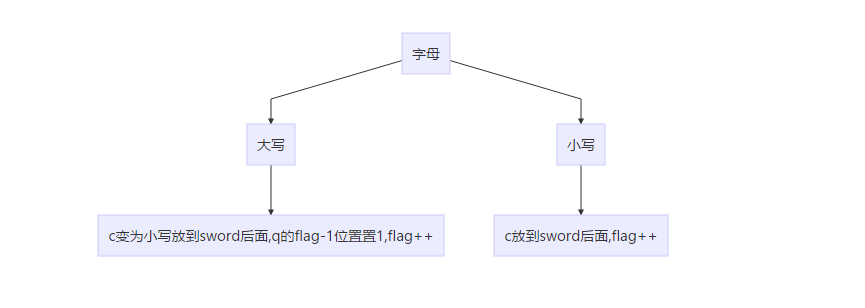
if ((c < 91 && c>64) || (c < 123 && c>96)) { / flag++; if (c < 91 && c>64) { c = c + 32; sword = sword + c; if (flag<128) q.set(flag - 1); } else sword.push_back(c);
读到数字。
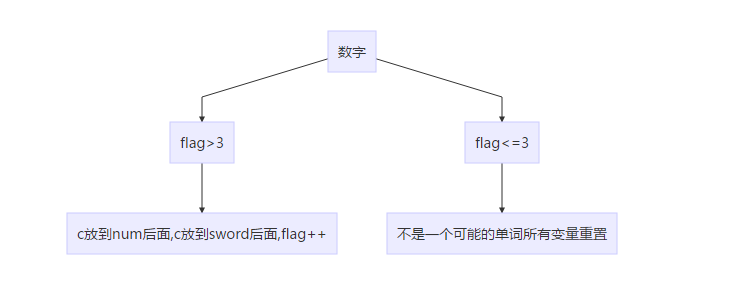
代码:
else if (c > 47 && c < 58) {
if (flag > 3) {
num = num + c;
sword = sword + c;
flag++;
}
else {
flag = 0;
sword = "";
q = 0;
num = "";
}
}
特殊字符是最麻烦的,因为要存储了。
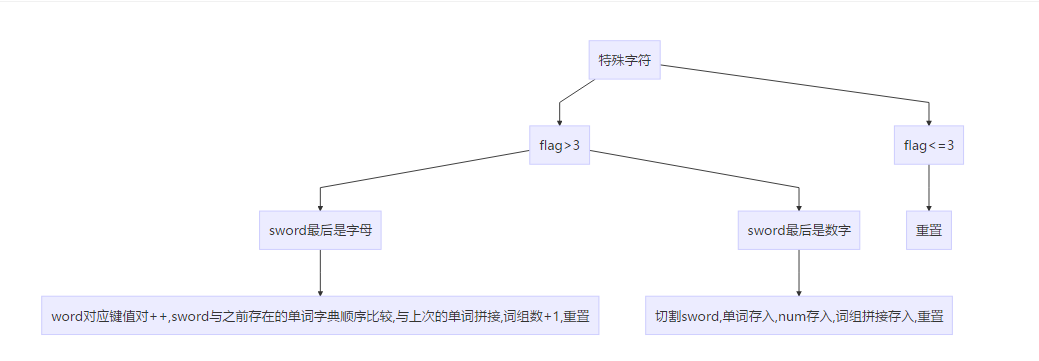
代码:
else { //特殊字符
if (flag > 3) {
if (sword[sword.length() - 1] < 123 && sword[sword.length() - 1]>96) //最后是字母
{
word[sword]++;
wordd[sword] = bitcmp(q, wordd[sword]);
wordend[sword] = "";//有纯单词,则按字典顺序只需要存后缀为空
sphrase = sphrase + " " + sword;
phrase[sphrase]++;
sphrase = sword;
}
else { //后缀为数字
sword = sword.substr(0, strlen(sword.c_str()) - strlen(num.c_str()));
word[sword]++;
it = wordend.find(sword);
if (it == wordend.end()) { //说明不存在这个数字后缀的单词
wordend[sword] = num;
}
else
{
wordend[sword] = wordend[sword].compare(num) > 0 ? num : wordend[sword];
}
wordd[sword] = bitcmp(q, wordd[sword]);
sphrase = sphrase + " " + sword;
phrase[sphrase]++;
sphrase = sword;
}
sword = "";
num = "";
q = 0;
flag = 0;
}
else {
flag = 0;
sword = "";
num = "";
q = 0;
}
}
注意,在文件的最后可能突然结束没有特殊字符,这时候就会跳出while(get(c)),sword,num等中可能还有有意义的值,所以跳出循环后要再跑一次特殊符号的逻辑。
以上应该说就是此次作业用时最多,花费最多的部分。
再有出彩的地方应该就是查找最大值,采用一个string[10]放top10字符串,int[10]放top10单词的数目,迭代器遍历,动态维护前十。
代码:
void top(unordered_map<string, int> & word) {
unordered_map<string, int>::iterator it = word.begin();
unordered_map<string, int>::iterator end = word.end();
int min = getwmin();
for (; it != end; it++) {
if (it->second > wnumtop[min]) {
topworld[min] = it->first;
wnumtop[min] = it->second;
min = getwmin();
}
}
}
其实前10用堆动态维护跑的最快,但看了下不是性能瓶颈就直接写数组了。
在DDL前5个小时,跟同学讨论中发现了更为简单的逻辑,去除bit位标志大小写的方法,转而只另用一个map来解决按字典顺序输出的问题,这是因为数字储存为字符串可以跟字母一块比较,这样键值为小写的单词,相对的储存当前字典顺序最靠前的单词,大大简化了以前先比字母再比数字的逻辑(主要是减少了分支),使得代码速度快了2s左右吧。bsword存储当前真实单词,sword存储当前单词的小写。
这样其实只有一个地方做了较大的修改,就是判定为单词然后遇到特殊符号储存的部分。
写入的时候判断逻辑:
if (flag > 3) { //遇到特殊字符,并且sword里面存了一个可以写入的单词
if (sword[flag - 1] < 123 && sword[flag - 1]>96) //sword最后为字母
{
word[sword]++; //对应单词数目++
string s = wordend[sword];
if (word_end[sword] == "") { //说明第一次写入这个单词
word_end[sword] = bsword; //直接写入真实单词
}
else {
word_end[sword] = s.compare(bsword) > 0 ? bsword : s; //否则真实单词要与之前储存的进行字典顺序比较
}
sphrase.push_back(' ');
sphrase.append(sword); //对应词组++
phrase[sphrase]++;
sphrase = sword;
}
else {
sword = sword.substr(0, strlen(sword.c_str()) - strlen(num.c_str())); //最后是数字,把数字去掉
word[sword]++; //对应单词数目++
string s = wordend[sword] ;
if (wordend[sword] == "") { //第一次写入
wordend[sword] = bsword;
}
else {
wordend[sword] = s.compare(bsword) > 0 ? bsword : s; //比较字典顺序
}
sphrase.push_back(' ');
sphrase.append(sword);
phrase[sphrase]++;
sphrase = sword;
}
sword = "";
bsword = "";
num = "";
flag = 0;
}
else {
flag = 0;
sword = "";
bsword = "";
num = "";
}
}
可见比起之前确实简化了许多。


