72. Edit Distance(编辑距离 动态规划)

Given two words word1 and word2, find the minimum number of operations required to convert word1 to word2.

You have the following 3 operations permitted on a word:

1. Insert a character
2. Delete a character
3. Replace a character

Example 1:

Input: word1 = "horse", word2 = "ros"
Output: 3
Explanation: 
horse -> rorse (replace 'h' with 'r')
rorse -> rose (remove 'r')
rose -> ros (remove 'e')

Example 2:

Input: word1 = "intention", word2 = "execution"
Output: 5
Explanation: 
intention -> inention (remove 't')
inention -> enention (replace 'i' with 'e')
enention -> exention (replace 'n' with 'x')
exention -> exection (replace 'n' with 'c')
exection -> execution (insert 'u'

 

 

1. 确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

 

---

2. 确定递推公式

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
    不操作
if (word1[i - 1] != word2[j - 1])
    增
    删
    换

3. dp数组如何初始化

再回顾一下dp[i][j]的定义：

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

 

4. 确定遍历顺序

从如下四个递推公式：

• dp[i][j] = dp[i - 1][j - 1]
• dp[i][j] = dp[i - 1][j - 1] + 1
• dp[i][j] = dp[i][j - 1] + 1
• dp[i][j] = dp[i - 1][j] + 1

可以看出dp[i][j]是依赖左方，上方和左上方元素的，如图：

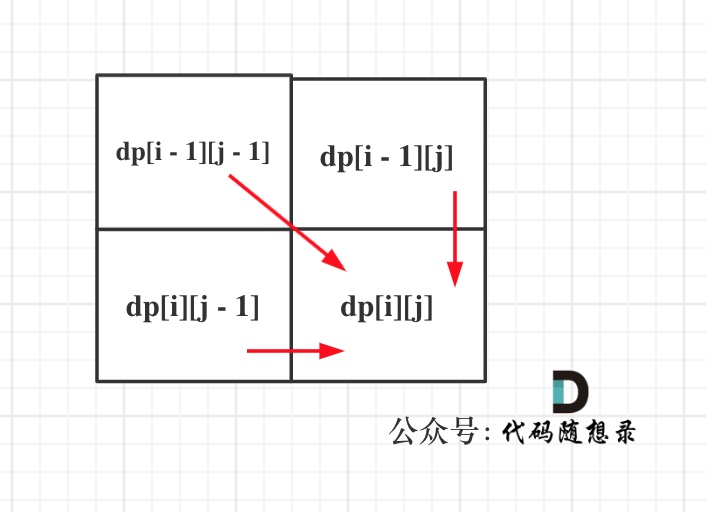
所以在dp矩阵中一定是从左到右从上到下去遍历。

 

 

 

 

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.size();
        int m = word2.size();
        int dp[n+1][m+1];
        for(int i = 0;i <= n;++i) dp[i][0] = i; // word1的子串（i->n）与 word2空字符串的编辑距离
        for(int j = 0;j <= m;++j) dp[0][j] = j;

        for(int i = 1;i <= n; ++i) {
            for(int j = 1;j<=m; ++j) {
                if(word1[i-1] == word2[j-1]) { //字符串下标从0开始。dp 下标从1开始。 
                    dp[i][j] = dp[i-1][j-1];
                }
                else {
                    // dp[i-1][j]  word1[i] 删除
                    // dp[i][j-1]. word2[j] 删除（等价于 word1增加）
                    // dp[i-1][j-1]. word1[i]、word2[j]选一个替换
                    dp[i][j] = 1 + min({dp[i-1][j],dp[i][j-1],dp[i-1][j-1]});
                }
            }
        }
        return dp[n][m];
    }
};

 

 

 

 

 

class Solution:

    def minDistance(self, x, y):
        """
        :type word1: str
        :type word2: str
        :rtype: int
        """
        m = len(x)
        n = len(y)
        dp = [[' '] * (n + 1) for i in range(m + 1)]

        for i in range(m + 1):
            dp[i][0] = i
        for j in range(n + 1):
            dp[0][j] = j

        for i in range(1, m + 1):
            for j in range(1, n + 1):
                if x[i - 1] == y[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1]
                else:
                    dp[i][j] = 1 + min(dp[i - 1][j], dp[i]
                                       [j - 1], dp[i - 1][j - 1])
        return dp[m][n]