42. 接雨水（dp or 双指针)

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example, 
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

 

 

 

class Solution {
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<int>l_max(n);
        vector<int>r_max(n);
        l_max[0] = height[0];
        r_max[n-1] = height[n-1];
        for(int i = 1; i <n ;i++) {
            l_max[i] = max(l_max[i-1],height[i]);
        }
        for(int i = n-2; i>=0; i--) {
            r_max[i] = max(r_max[i+1],height[i]);
        }

        int res = 0;
        for(int i = 0; i <n;i++) {
            res += min(l_max[i],r_max[i]) - height[i];
        }
        return res;
    }
};

 

 

 

 

 

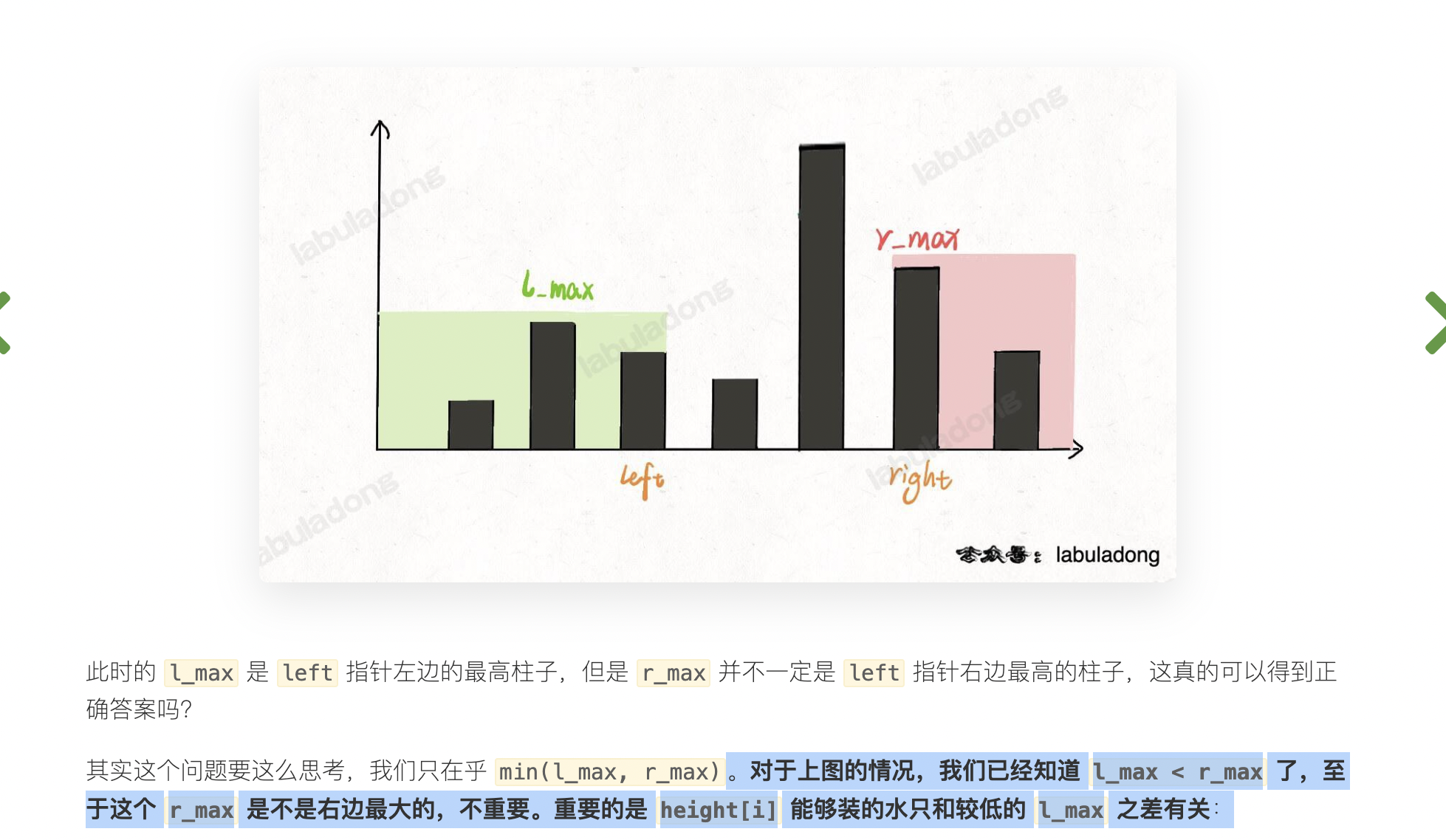
。对于上图的情况，我们已经知道 l_max < r_max 了，至于这个 r_max 是不是右边最大的，不重要。重要的是 height[i] 能够装的水只和较低的 l_max 之差有关：

class Solution:
    def trap(self, height: List[int]) -> int:
        n = len(height)
    
    
        l = 0 
        r = len(height) -1
        l_max = height[0]
        r_max = height[-1]

        res = 0
        while l<=r:
            l_max = max(l_max,height[l])
            r_max = max(r_max,height[r])
            cur_rea = 0
            if l_max < r_max:
                res+=(l_max-height[l])
                l+=1
            else:
                res+=(r_max-height[r])
                r-=1

        
        return res

 

 

 

 

 

 

 

 

单调栈：

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> stk;
        int res = 0;
        for(int i = 0; i < height.size();i++) {
            while(!stk.empty() && height[i] > height[stk.top()]) {
                int top = stk.top();
                stk.pop();
                if (!stk.empty()) {
                    int w = i - stk.top()-1;
                    int h = min(height[i],height[stk.top()]) - height[top];
                    res += w*h;
                }                
            }
            stk.push(i);
        }
        return res;

    }
};