[算法][递归] 棋盘覆盖
>_<: 问题描述：
在一个2k×2k 个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。
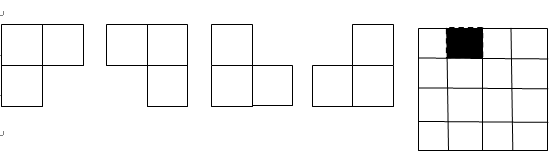
>_<: 解决方法：
当k>0时，将2^k X 2^k 棋盘分割为4个2^(k-1) X 2^(k-1)子棋盘，特殊格必位于四块小的棋盘之一中，其余3个子棋盘无特殊方格，为了将这3个无特殊的格子棋盘转化为特殊棋盘，我们可以用一个L型的骨牌覆盖这3个较小的企盼汇合处，从而将问题转化为4个较小规模的企盼覆盖问题，递归使用这种分割，直至棋盘划分为1的棋盘。
1 #include<iostream> 2 #include<iomanip> 3 using namespace std; 4 int tile=1; //L型骨牌的编号(递增) 5 int board[100][100];//棋盘 6 /***************************************************** 7 * 递归方式实现棋盘覆盖算法 8 * 输入参数： 9 * tr--当前棋盘左上角的行号 10 * tc--当前棋盘左上角的列号 11 * dr--当前特殊方格所在的行号 12 * dc--当前特殊方格所在的列号 13 * size：当前棋盘的:2^k 14 *****************************************************/ 15 void chessBoard(int tr,int tc,int dr,int dc,int size){ 16 if(size==1)//棋盘方格大小为1,说明递归到最里层 17 return; 18 int t=tile++;//每次递增1 19 int s=size/2;//棋盘中间的行、列号(相等的) 20 21 //检查特殊方块是否在左上角子棋盘中 22 if(dr<tr+s && dc<tc+s)//在 23 chessBoard(tr,tc,dr,dc,s); 24 else{//不在，将该子棋盘右下角的方块视为特殊方块 25 board[tr+s-1][tc+s-1]=t; 26 chessBoard(tr,tc,tr+s-1,tc+s-1,s); 27 } 28 29 //检查特殊方块是否在右上角子棋盘中 30 if(dr<tr+s && dc>=tc+s)//在 31 chessBoard(tr,tc+s,dr,dc,s); 32 else{//不在，将该子棋盘左下角的方块视为特殊方块 33 board[tr+s-1][tc+s]=t; 34 chessBoard(tr,tc+s,tr+s-1,tc+s,s); 35 } 36 37 //检查特殊方块是否在左下角子棋盘中 38 if(dr>=tr+s && dc<tc+s)//在 39 chessBoard(tr+s,tc,dr,dc,s); 40 else{//不在，将该子棋盘右上角的方块视为特殊方块 41 board[tr+s][tc+s-1]=t; 42 chessBoard(tr+s,tc,tr+s,tc+s-1,s); 43 } 44 45 //检查特殊方块是否在右下角子棋盘中 46 if(dr>=tr+s && dc>=tc+s)//在 47 chessBoard(tr+s,tc+s,dr,dc,s); 48 else{//不在，将该子棋盘左上角的方块视为特殊方块 49 board[tr+s][tc+s]=t; 50 chessBoard(tr+s,tc+s,tr+s,tc+s,s); 51 } 52 } 53 54 void main(){ 55 while(true){ 56 memset(board,0,sizeof(board)); 57 tile=1; 58 59 int size; 60 61 cout<<"输入棋盘的size(大小必须是2的n次幂): "; 62 cin>>size; 63 int index_x,index_y; 64 cout<<"输入特殊方格位置的坐标: "; 65 cin>>index_x>>index_y; 66 67 chessBoard (0,0,index_x,index_y,size); 68 69 cout<<endl; 70 for(int i=0;i<size;i++){//输出棋盘覆盖 71 for(int j=0;j<size;j++ ) 72 cout<<setw(3)<<board[i][j]<<" "; 73 cout<<endl; 74 } 75 cout<<endl; 76 } 77 }
