进阶篇:6.2)公差的正态分布与CPK与制程能力(重要)
本章目的:明确公差分布(Tolerance Distribution)也有自己的形状,了解CPK概念。
1.正态分布(常态分布)normal distribution的概念
统计分析常基于这样的假设:零件在大批量生产时,其尺寸在其公差范围内呈正态分布(常态分布)normal distribution。
事实也是如此,针对一个零件尺寸,在一定制造条件下制造并测量无数个零件,并记录相同尺寸出现的频率,可以绘制出一张尺寸大小的频率图,这张图纸就是正态分布图。如下面两张图所示(一简一繁)。
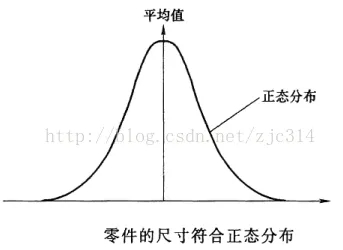

多数的零件尺寸值会向着图形的中心,即尺寸的平均值聚集,离平均值越远,该尺寸出现的可能性就越小。
这里就有两个重要值,中间值μ与标准差σ。即公差形状的中心和范围,各本书中关于这两个值的解释和标注都有所不同,但工程师要注意其本质。
中间值μ:曲线对称轴的位置,这决定了整条曲线的位置。
标准差σ:由中间值到曲线的曲率正负号改变点的距离,这决定了曲线的分散或集中程度。
补充解释如下图(spc手册):
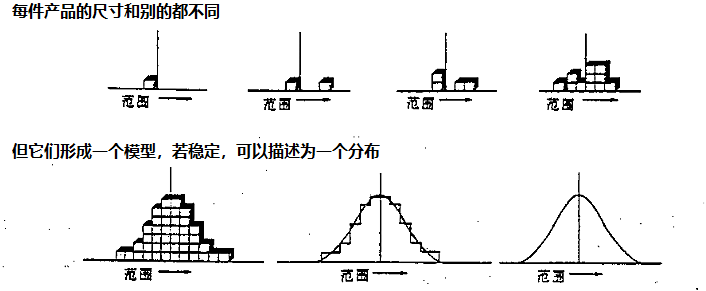
正态分布,即是公差的形状,需要熟记于心。
从正态分布的概念看出,图纸公差标注只代表的是范围值,却不能规定制造零件的合格率形状。
所以我们在图纸绘制时,标注的公差并不能约束它的分布形态。但标注时就需要了解统计分析,遵守基本的公差分布情况。
比如单边公差标注,如1(+0.5/0)等,并不能约束所有制造的零件尺寸又在你的公差范围内,同时又偏向一边,不合理的。如下图:
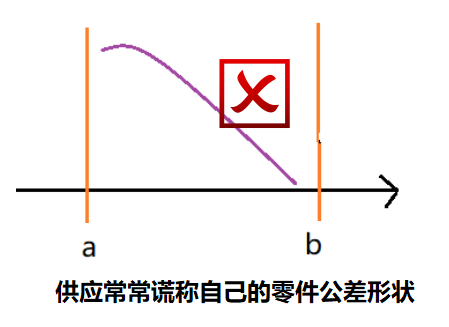
很多供应商声明它们在制作零件时既能保证尺寸在[a,b]范围以内,又能保证大部分的零件靠近a值。这并不符合正态分布的概念。
供应商会告诉你他能做到很多事情,却常常隐瞒你要付出的代价。
1.1 各种公差分布(Tolerance Distribution)的形态
公差分布型态(Tolerance Distribution)不只是一种。如下图所示:

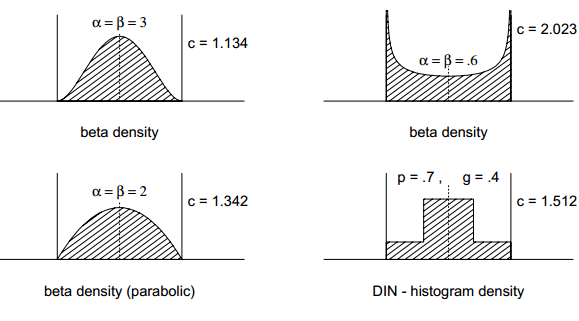
图1为正态分布(或称之为常态分布),这是大多数零件生产时候会出现的情况。但这种情况并不是唯一的,极端情况下也会出现其他的公差分布形态。我们很多时候进行统计分析时都是运用正态分布图,但也不要忘记其他公差分布的情况。
就作者的理解,其他有规律的公差形状,如倒钟形或双峰形等,也可以算是正态分布的变种。所以应该也能进行统计分析的计算(这些知识作者就没有研究这么深了)。
2.理解正态分布存在的价值
有些机械设计师不明白,我为什么要理解公差的分布形状,制造方不是只要制造尺寸公差合格的零件就行了么,尺寸不合格的零件,当然不要了。
这个概念其实不算错,但现实不会如此简单。
假如量产100万件产品,成本是10元,合格率100%。但当成本降低至8元时,而合格率为99.9999%。你是老板,你会怎么选?
一般人当然会选后者。
而大幅度降低成本,却只会小幅度增加不良率的依据,正是正态分布图。(cpk是要和正态分布要一起讲的概念)
又但是,这件事不绝对,有些产品的正太分布是水平线的形状或倒V字,这时候降低生产精度和成本,会大幅度提高不良率,就不合适了。
而如何正确控制不良率和成本,就是质量管理的作用。设计也要参与其中,产品设计就是在成本与质量的之间衡量,而且也是性价比最好的手段(虽然不敢称之为最快或最好的手段,但设计绝对是性价比最高的手段)
设计者为什么可以敢于设计一个可能有错误的产品,制造方为什么有理由制造错误的产品,检测人员为什么能放过错误的产品。
请看所有万恶之源:正态分布与cpk。
3.cpk是基于正态分布原理
cpk的统计是基于零件的公差分布是正态分布(Tolerance Distribution)。
对于非正态分布的统计分析,是否能用cpk,作者也不能肯定。(没有对应的中文资料,统计技术也是在发展的)
4.CPK的基础知识点
1)Cpk (Complex Process Capability index .)的中文定义为:制程能力指数,是某个工程或制程水准的量化反应,也是工程评估的一类指标。
2)同Cpk息息相关的两个参数:Ca , Cp.
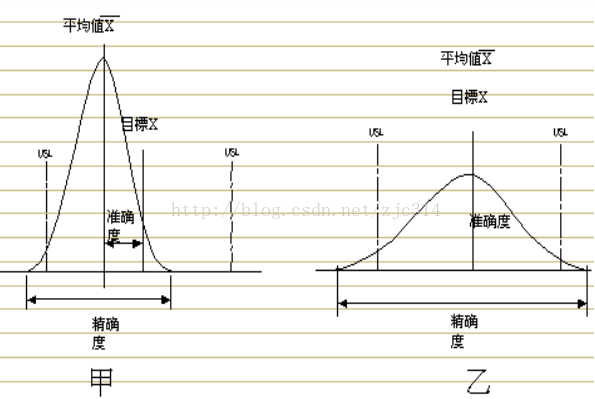
Ca: 制程准确度。 在衡量「实际平均值」与「规格中心值」之一致性。对於单边规格,因不存在规格中心,因此不存在Ca;对於双边规格,Ca=(ˉx-U)/(T/2)。
Cp: 制程精密度。 在衡量「规格公差宽度」与「制程变异宽度」之比例。对於单边规格,
只有上限和中心值,Cpu = | USL-ˉx | / 3σ。
只有下限和中心值,Cpl = | ˉx -LSL | / 3σ
对於双边规格:Cp=(USL-LSL) / 6σ
3)Cpk, Ca, Cp三者的关系: Cpk = Cp * ( 1 - |Ca|),Cpk是Ca及Cp两者的中和反应,Ca反应的是位置关系(集中趋势),Cp反应的是散布关系(离散趋势)。
//也就是说,中心值μ越是接近于理论值,Ca越小。越是集中,Cp越大。这样的趋势,也就是cpk是越好的。
4)当选择制程能力Cpk来作管控时,应以成本做考量的首要因素?还有是其品质特性对后制程的影响度。
5)计算取样数据至少应有20~25组数据,方具有一定代表性。
6)计算Cpk除收集取样数据外,还应知晓该品质特性的规格上下限(USL,LSL),才可顺利计算其值。
7)首先可用Excel的“STDEVP”函数(注:应该是“STDEV”,可参考minitab计算出的数据。excel2007及早期版本与STDEV.P计算值相同)
自动计算所取样数据的标准差(σ),再计算出规格公差(T),及规格中心值(U). 规格公差T=规格上限-规格下限;规格中心值U=(规格上限+规格下限)/2;
5.cpk评级标准及处理
1)依据公式:Ca=(X-U)/(T/2) , 计算出制程准确度:Ca值 (X为所有取样数据的平均值)
Ca的评级标准及处理:
| 等级 | Ca值 | 处理原则 |
| A | |Ca|≤12.5% | 作业员遵守作业标准操作并达到要求,需继续保持。 |
| B | 12.5%≤|Ca|≤25% | 有必要将其改进为A级。 |
| C | 25%≤|Ca|≤50% | 作业员可能看错规格或不按作业标准操作。须检讨规格及作业标准。 |
| D | 50%≤|Ca| | 应采取紧急措施全面检讨所有可能影响之因素,必要时得停止生产。 |
2)依据公式:Cp =T/6σ , 计算出制程精密度:Cp值
Cp的评级标准及处理:
| 等级 | Cp值 | 处理原则 |
| A+ | Cp≥1.67 | 无缺点。可考虑降低成本。 |
| A | 1.33≤Cp≤1.67 | 状态良好维持现状。 |
| B | 1.00≤Cp≤1.33 | 改进为A级。 |
| C | 0.67≤Cp≤1.00 | 制程不良较多,须提升能力。 |
| D | Cp≤0.67 | 制程能力歹差,应考虑重新整改设计程程。 |
3) 依据公式:Cpk=Cp(1-|Ca|) , 计算出制程能力指数:Cpk值
4)Cpk的评级标准:(可据此标准对计算出之制程能力指数做相应对策)
| 等级 | Cpk值 | 处理原则 |
| A++ | Cpk≥2.0 | 特优,可考虑成本的降低 |
| A+ | 2.0 > Cpk ≥ 1.67 | 优,应当保持之 |
| A | 1.67 > Cpk ≥ 1.33 | 良,能力良好,状态稳定,但应尽力提升为A+级 |
| B | 1.33 > Cpk ≥ 1.0 | 一般,制程因素稍有变异即有产生不良的危险,应利用各种资源及方法将其提升为 A级 |
| C | 1.0 > Cpk ≥ 0.67 | 差,制程不良较多,必须提升其能力 |
| D | 0.67 > Cpk | 不可接受,其能力太差,应考虑重新整改设计制程。 |
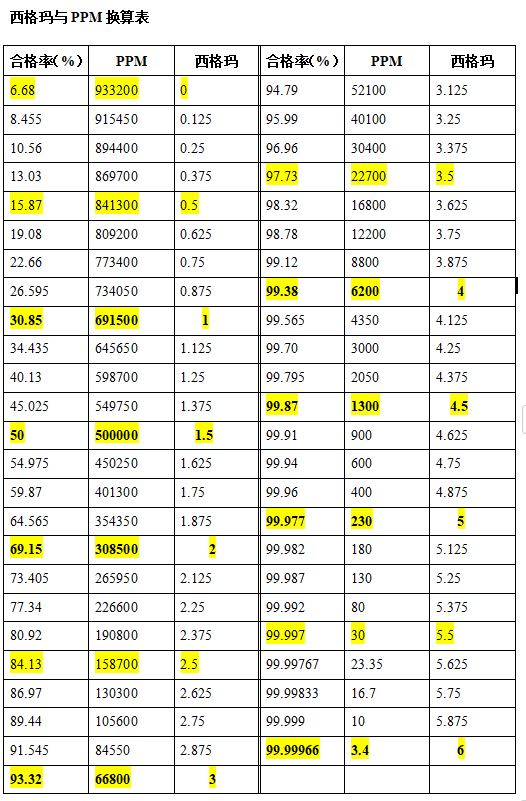
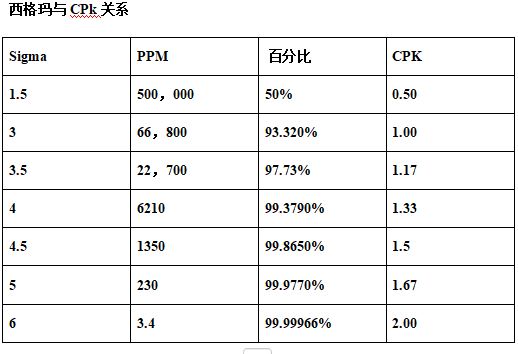
5) Cpk、西格玛σ,PPM,(parts per million 百万分之),合格率。
作者看过很多资料,总感觉这些换算的表格不一致?不知道是不是因为中间值u的1.5σ偏移的问题。
下面这份表格是作者现在最认同的,毕竟6σ表示百万分之3.4件不合格。
6)CPK与PPK的不同
CPK与PPK都是表示制程能力的参数,PPK中添加了对过程特殊原因的关注,是描述过程性能的指标,两者的不同在于取标准差的算法不同σ,其余计算方法实际上是一样的。现实中也常常用cpk代替PPK的运算。
5.cpk是针对特征而言的
有些质量管理人员讲解cpk单指尺寸,但实际上cpk与正态分布图的应用范围是很广的。比如材料的某些特性也是呈正态分布的,再比如大多数产品的合格率也是呈正态分布的。
6.cpk运用时间点
如图所示,早期就可以在模具样品中运用了。
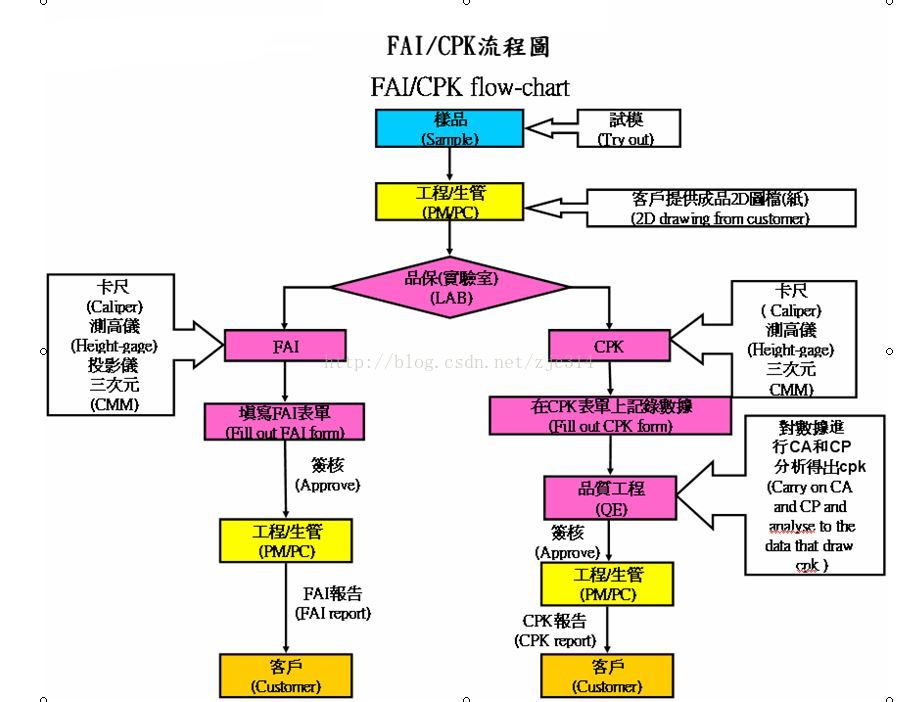
FAI是为了证明:这是一个正确的零件/产品。
CPK是为了证明:后续大量生产,也可以保证质量稳定。
只有先做好这两点,以后量产的时候,才能检验关键尺寸就能成为质量稳定的依据。
7.cpk统计表格的运用
现在cpk统计并非需要手工计算,简单的方法可以运用cpk统计的表格(网上可以简单地找到,作者分享里也有),如下图所示:
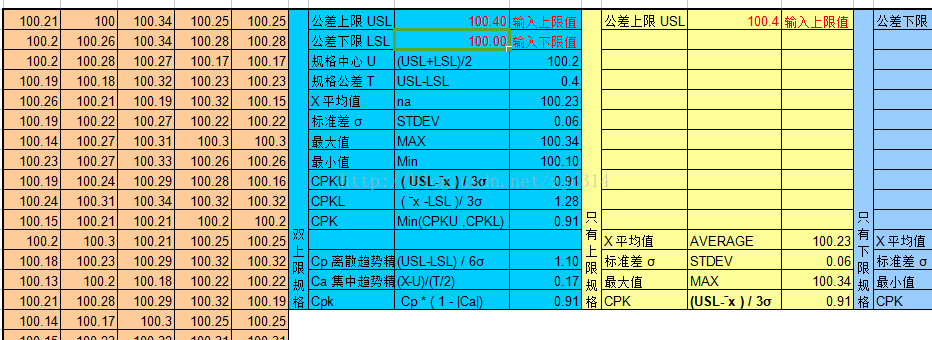
8.cpk章节对应的资料汇总




 浙公网安备 33010602011771号
浙公网安备 33010602011771号