进阶篇：5.3.2）6σ公差分析法(6σ)

本章目的：了解6σ公差分析法，运用6σ公差分析法。

 

1.定义

6σ公差分析法：6σ公差分析法是统计公差法的一种，是将尺寸链内尺寸的不同制程能力考虑在内，通过优化尺寸链公差参数达到目标尺寸为6σ的方法。

//良品率未必一定是6σ，符合公司要求合适的良品率即可。

从均方根章节中知道，均方根法假设制程能力是相同的。

但在实际当中,更加有可能的是，用来公差叠加分析的特征制程，通常都没有控制在同一个等级。公差分析里面的公差很可能是有几个是±2σ,有几个是±3σ。

6σ公差分析法，其就允许每个组中的零部件有不同的制程水平,甚至是不同的公差分布型态。

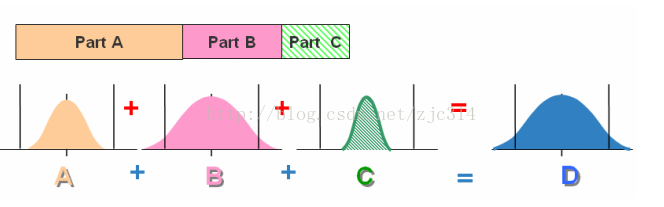
不同的制程水平：即拥有不同的Ca及Cp。

不同的不同的公差分布型态：如下小结所示。

 

1.1 各种公差分布的形态

公差分布型态（Tolerance Distribution）不只是一种。如下图所示：

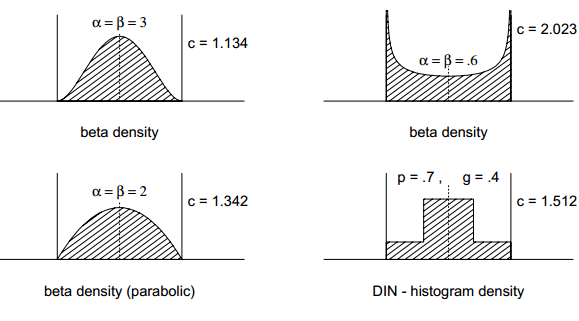
 图1为正态分布（或称之为常态分布），图2为均匀分布。这两种比较常用。

//以前作者关于公差分布型态有些写错了，请注意。作者以前一直以为均匀分布等有规律的公差分布形态就是正态分布的一种。虽然说不是不能这么看，但不对。

 

1.2 计算公式

暂无。

其公式推演如下：

公式推演有助于了解方法本质，但缺少合适的6σ公差分析法的公式及推演，以后再写！！！

//作者暂时也找不到比较清晰明确的。

 

2.6σ公差分析法计算实例

题目：

A尺寸的值和公差为54.00±0.20，cp为1，cpk为0.75；

B为12.00±0.10，C为13.00±0.10，D为16.00±0.15，E为12.50±0.10，四个零件的cp为1.33.cpk为1;

五个零件的公差分布模型均为normal；

间隙Gap的要求为，0≤Gap≤1。

利用6σ公差分析法求关键尺寸X的名义值和公差，cpk。（将这一题与极值法，均方根法比较）

 

 计算过程：
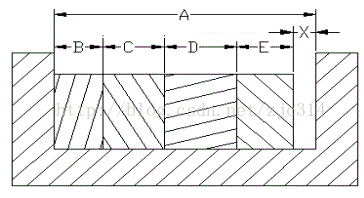
①计算X的名义值：
DX= DA+ DB+ DC+ DD+ DE
= 54.00 + (-12.00) + (-13.00) + (-16.00) + (-12.50)
= 54.00 -12.00 -13.00 -16.00 -12.50
= 0.50 毫米
②计算X的公差

利用表格计算的结果如上，Tasm=0.53.

间隙X=0.5±0.53，cpk=1.42；

 

3.6σ公差分析法的要点

缺少！（以后补齐）

 

3.1 六西格玛机械公差设计分析的假设前提是

（1）变量之间相互独立，均值和方差相互独立；

（2）所有零件的尺寸均服从正态分布；（这一条有待讨论）

（3）σ用来描述变异性，由于材料和制造过程中不可避免的变异，采用1.5σ作为标准漂移来计算公差域之外的概率。

 //这一条也很麻烦，因为6σ这个概念一直有争议。

 

3.2 6σ法中的1.5σ偏移的由来

通常工程领域，制造制程常常传统地设置满足有效等级3σ。大约百万个产品中2700个不良。尽管这些超出地产品起初看起来非常良好，但在一些产品领域，越发不足。除此之外，从长期来看几乎不可能保证制程特性曲线地中心值完全在容许范围地中心。以防大批量生产时的制程特性曲线的中心值随着时间的推移而偏移，由于变化因子的影响（错误的组装，工具和夹具的磨损，温度变化等等。）1.5σ的偏移是典型的，对于接近3σ等级的制程能力，表现爲超出公差的比率爲百万分之67000。很明显在此等级的制程损坏是不可接受的。因此，最近"6σ"的方法越来越被广泛使用在评估制程质量上。方法的概念是获得制程特性的中心值是在距离两个公差极限值6σ范围内。在此有效制程条件下，即使1.5σ的偏移产生，也可保证百万分之3.4的超出公差的比率。

 

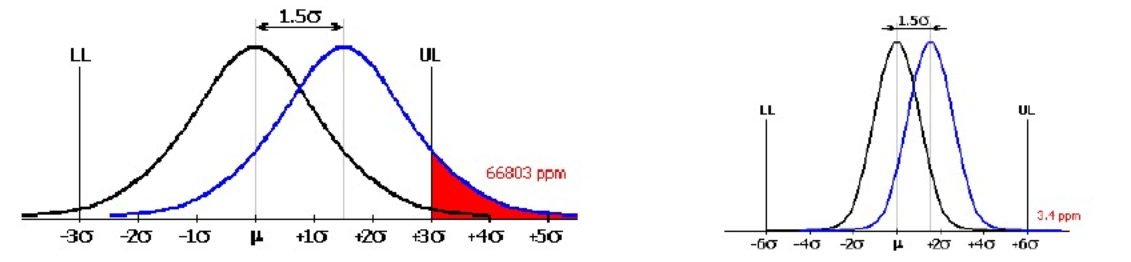
3.3 1.5 sigma shift

The statistician Donald J. Wheeler has dismissed the 1.5 sigma shift as "goofy" because of its arbitrary nature.[49] Its universal applicability is seen as doubtful.
The 1.5 sigma shift has also become contentious because it results in stated "sigma levels" that reflect short-term rather than long-term performance: a process that has long-term defect levels corresponding to 4.5 sigma performance is, by Six Sigma convention, described as a "six sigma process."The accepted Six Sigma scoring system thus cannot be equated to actual normal distribution probabilities for the stated number of standard deviations, and this has been a key bone of contention over how Six Sigma measures are defined. The fact that it is rarely explained that a "6 sigma" process will have long-term defect rates corresponding to 4.5 sigma performance rather than actual 6 sigma performance has led several commentators to express the opinion that Six Sigma is a confidence trick.

 //1.5σ偏移是有缺陷的，不要太迷信。

 

4.运用均方根法公差分析完整流程

4.1 查看公差分析总章流程

1.定义公差分析的目标尺寸和判断标准（对于完整的公差分析，最难和最容易忽略的一步）；

2.建立闭合尺寸链；

3.将非对称公差转成对称公差；

4.判断尺寸链中尺寸的正负；

5.计算目标尺寸的名义值；

6.选用公差分析的方法

7.公差分析的计算；

8.判断和优化；

9.公差分析结果图纸标注，统计公差法标注对应符号。

 

4.2 依次按流程设计，流程6公差分析方法选用均方根法

1）定义公差分析的目标尺寸和判断标准（对于完整的公差分析，最难和最容易忽略的一步）

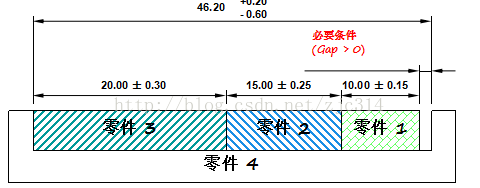
如下图，
四个零件的公差分布模型均为normal，cp为1.33，cpk为1；
其目标尺寸为装配间隙Gap，判断标准为：0≤Gap≤2(2为假定值)，cpk为1.67。

这些在公差分析目标汇总表中必须要有。

2）建立闭合尺寸链

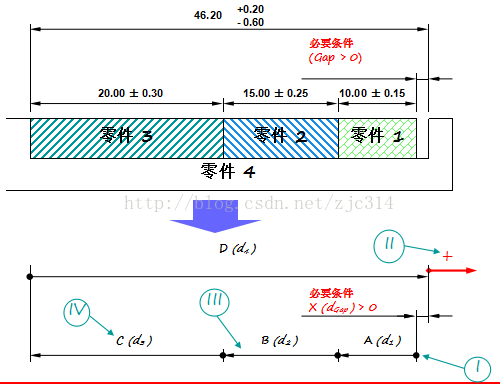
3）将非对称公差转成对称公差

4）判断尺寸链中尺寸的正负

D=A+B+C+X，所以目标尺寸X=+D-C-B-A。

5）计算目标尺寸的名义值

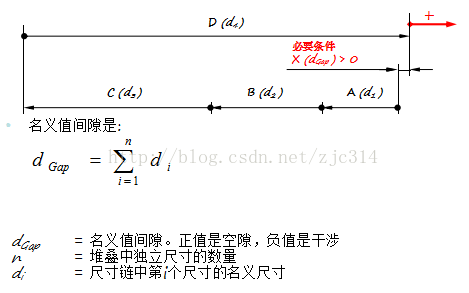
名义值间隙：dGap= + 46.00- 10.00 - 15.00 - 20.00  = 1.00

这时候可以用3d软件检验其间隙是否为1，前提是你的3d图纸都是基于对称公差绘制的。

6）选用公差分析的方法

选定6σ公差分析法。

7）公差分析的计算

名义间隙的公差

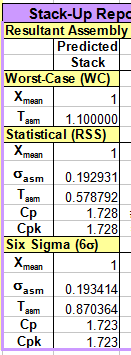
由表格计算的，目标尺寸为Gap=1±0.87；（极值法计算值为1±1.10，均方值为1±0.58）

最大值为1.87，最小值为0.13；

8）判断和优化

因为目标尺寸的判断标准为0≤Gap≤2(2为假定值),所以就公差分析的结果而言符合要求。

cpk为1.72>1.67(5σ)，一般而言也符合制造的要求（厂商有特殊要求另算）。

但从题上可知，6σ公差分析法对各个零件的制程控制有各种假设，所以为了使实际值符合计算要求，就需要进行严格的制程管控（统计公差法都需要）。

9）公差分析结果图纸标注，统计公差法标注对应符号

6σ公差分析法是统计公差法，对应分配的零件公差需要标注统计公差符号，如下图：

除此之外公差分析表格需要提高给质量管理，正确进行质量管控。

 

5.6σ公差分析法运用注意点

5.1 公差分析工具

①手工. （实在是不建议了）

②用电子数据表。（作者的网盘的就有，希望大家能多多练习，这方面作者不会吝啬）

公差分析表格版本一：

公差分析表格版本二：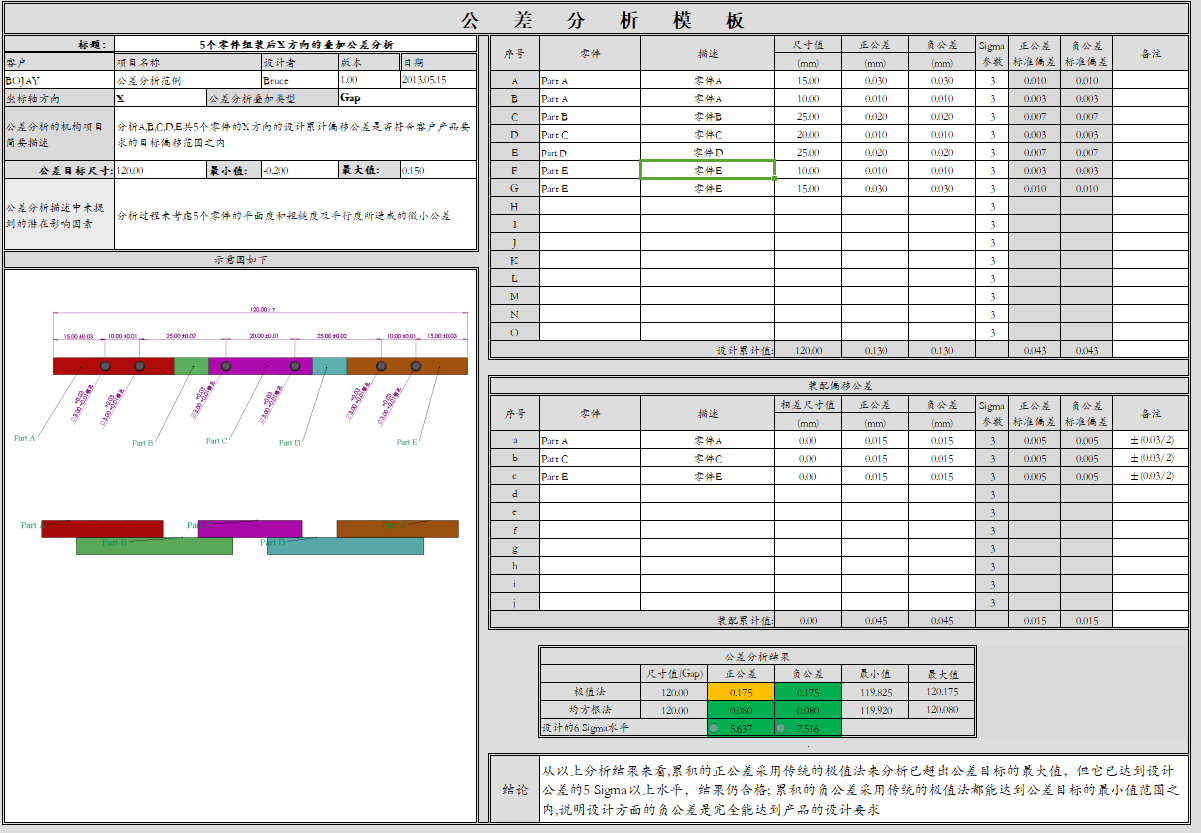


公差分析表格版本三：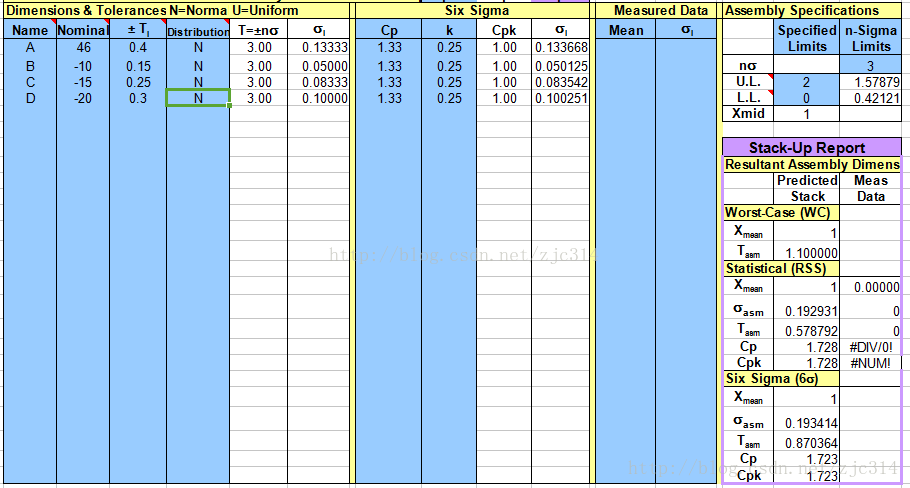

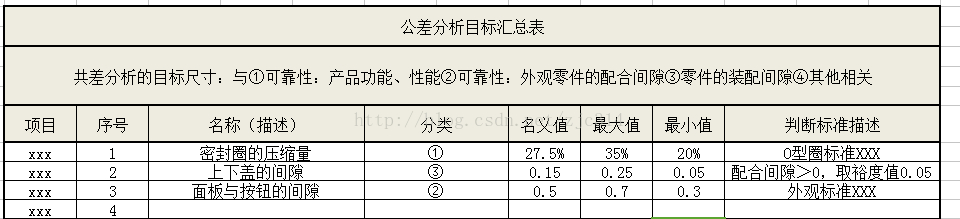
公差分析目标汇总表：

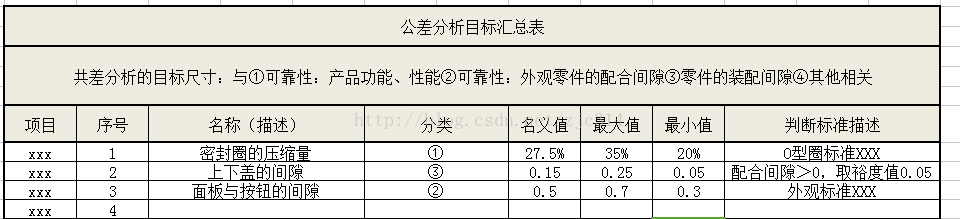
③用公差分析软件，比如 VisVSA™.

作者倒是希望能用前端做一个公差分析的软件，人人都能用。

 

5.2 无论你最后采取什么办法，极值法请优先运用一遍。

图纸上的公差最后采用哪种办法得到的值，务必慎重。

 

6.6σ公差分析法章节小记

公差分析本来就是一种比较难以用的上的方法，极值法就用的很少，均方根法就更少了。至于6σ公差分析法，作者就没有见过哪家公司用过。可能这真的对公司的质量管理要求比较高吧。

若从实际出发的话，作者还是建议务实极值法。等所有的一个产品的所有的公差分析都用极值法做完了，公司和自己都还有裕度，那么，在用均方根或6σ公差或其他公差分析法，这样比较好。

当然，这是自己的胡说，不理也行。