算法基础——列表排序

目录

　　LOW B 三人组

　　　　　　冒泡排序

　　　　　　选择排序

　　　　　　插入排序

　　NB 三人组

　　　　　　快速排序

　　　　　　堆排序

　　　　　　归并排序

　　其他

　　　　　　希尔排序

　　　　　　计数排序

 

 

列表排序即将无需列表变为有序，Python的内置函数为sort()。应用的场景主要有：各种榜单、各种表格、给二分查找用、 其他算法用等等。

有关列表排序的算法有很多，主要分为：

  • low B三人组： 冒泡排序、 选择排序、 插入排序

  • NB三人组： 快速排序、 堆排序、 归并排序

  • 其他排序算法： 计数排序、 希尔排序、 桶排序

算法排序的关键点在于有序区和无序区，我们将一个待排序的列表定为无序区，依次取出其中的元素进行排序，用于存放已排好序的元素的区域称为有序区

为了更形象的表示出每个排序算法的用时，我们先写一个用于计算时间的装饰器预备上

#在timewrap.py中：
import time


def cal_time(func):
    def wrapper(*args, **kwargs):
        t1 = time.time()
        result = func(*args, **kwargs)
        t2 = time.time()
        print("%s running time: %s secs." % (func.__name__, t2-t1))
        return result
    return wrapper
timewrap.py

 

Low B 三人组

　　Low B三人组分别指冒泡排序、 选择排序、 插入排序

　　冒泡排序（Bubble Sort）的思想（这里用升序举例，即排序后的结果为从小到大）是将一个待排序的列表理解为垂直结构，索引为0的元素在最下面。然后从索引为0的位置的元素开始，一次向上比较，若大于上面一个元素则两个元素交换位置（可以理解为下面的泡泡冒了上来），直到遇到比它大的元素或到达最顶端（即该元素为列表中的最大值）后停止。若该数到达最顶端，则继续由索引为0的元素重复上述冒泡运动；若遇到更大的元素，则由该大元素向上冒。冒泡排序总的平均时间复杂度为  ，空间复杂度：O(1)

冒泡排序算法的运作如下：（从后往前）
  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

　　冒泡排序是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较，交换也发生在这两个元素之间。所以，如果两个元素相等，是不会发生交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

文字撸不明白的可看原理图，如下：

　　　　　　　　　　　　　　　　　　　　

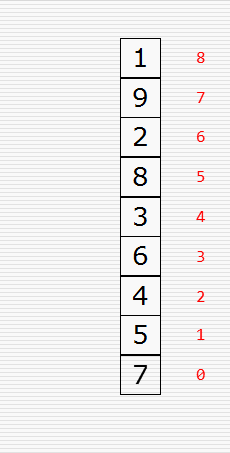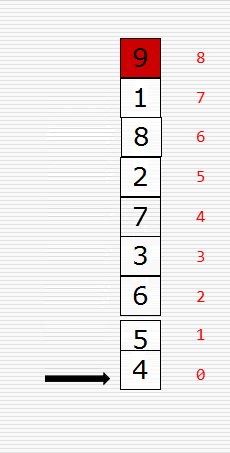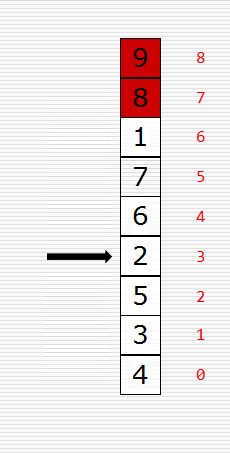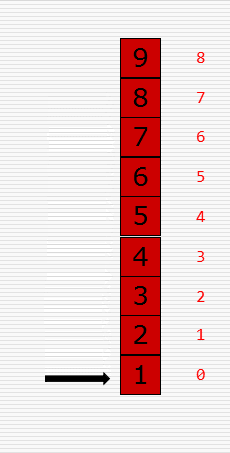
知道了原理后我们来写代码

def bubble_sort(li):
    for i in range(len(li)-1):#i是索引，表示趟数，第i趟时无序区(0,len(li)-i)
        for j in range(len(li)-i-1):#j是除去i个元素后的列表的索引（循环进行了几次就说明有几个元素已经被排好序）
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

如果冒泡排序执行了一趟而没有交换发生，说明该列表已经是有序状态，可以直接结束算法。所以我们可以将上述代码进行优化:

import random
from timewrap import *

@cal_time
def bubble_sort_2(li):
    for i in range(len(li) - 1):
        # i 表示趟数
        # 第 i 趟时： 无序区：(0，len(li) - i)
        change = False
        for j in range(0, len(li) - i - 1):
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                change = True
        if not change:
            return

li = list(range(10000))

bubble_sort_2(li)#bubble_sort_2 running time: 0.0010001659393310547 secs.
print(li)#0~9999已排好序

 

　　选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法（比如序列[5， 5， 3]第一次就将第一个[5]与[3]交换，导致第一个5挪动到第二个5后面）。选择排序总的平均时间复杂度为  ，空间复杂度：O(1)

　　思想：一趟遍历记录最小的数，放到第一个位置； 再一趟遍历记录剩余列表中最小的数，继续放置；

　　选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n-1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果一个元素比当前元素小，而该小的元素又出现在一个和当前元素相等的元素后面，那么交换后稳定性就被破坏了。比较拗口，举个例子，序列5 8 5 2 9，我们知道第一遍选择第1个元素5会和2交换，那么原序列中两个5的相对前后顺序就被破坏了，所以选择排序是一个不稳定的排序算法。

选择排序代码如下：

import random
from timewrap import *

@cal_time
def select_sort(li):
    for i in range(len(li) - 1):
        # i 表示趟数，也表示无序区开始的位置
        min_loc = i   # 最小数的位置
        for j in range(i + 1, len(li) - 1):#去除已经归为的最小数
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]


li = list(range(10000))
select_sort(li)#select_sort running time: 9.220226049423218 secs.
print(li)#0~9999已排好序

 

　　思路：列表被分为有序区和无序区两个部分。最初有序区只有一个元素。 每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。插入排序总的平均时间复杂度为  ，空间复杂度：O(1)

可以理解为扑克牌抓牌的过程

　　　　　　　　　　　　　　

基本代码如下：

import random
from timewrap import *

@cal_time
def insert_sort(li):
    for i in range(1, len(li)):
        # i 表示无序区第一个数
        tmp = li[i] # 摸到的牌
        j = i - 1 # j 指向有序区最后位置
        while li[j] > tmp and j >= 0:
            #循环终止条件： 1. li[j] <= tmp; 2. j == -1
            li[j+1] = li[j]
            j -= 1
        li[j+1] = tmp


li = list(range(10000))
insert_sort(li)#insert_sort running time: 0.003001689910888672 secs.
print(li)#0~9999已排好序

 

 

NB 三人组

　　NB三人组分别是： 快速排序、 堆排序、 归并排序

　　快速排序（Quicksort）是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

原理图如下：

　　　　　　　　　　

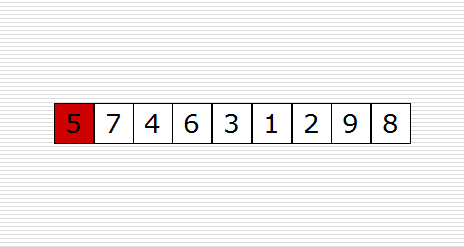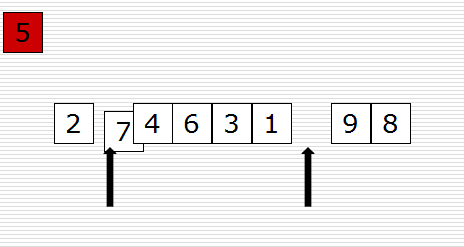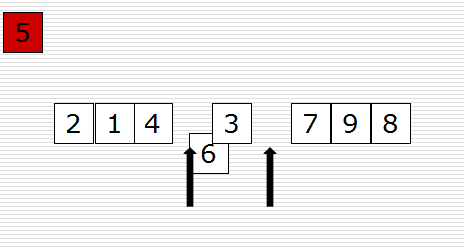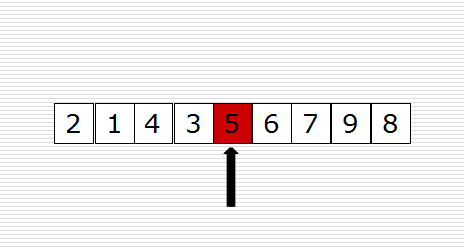
示例代码如下：

import random
from timewrap import *
import copy
import sys


sys.setrecursionlimit(100000)#修改递归最大深度，默认为997

def partition(li, left, right):
    # ri = random.randint(left, right)
    # li[left], li[ri] = li[ri], li[left]
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:
            right -= 1#找下一个
        li[left] = li[right]#while条件不成立，说明右边比temp小，右边数与temp的位置交换
        while left < right and li[left] <= tmp:
            left += 1
        li[right] = li[left]#while条件不成立，说明左边比temp大，左边数与temp的位置交换
    li[left] = tmp
    return left
#修改上面的 <= 和 >= 即可由将列表由升序排变为降序排

def _quick_sort(li, left, right):
    if left < right:    # 至少有两个元素
        mid = partition(li, left, right)
        _quick_sort(li, left, mid-1)#左边进行快排递归
        _quick_sort(li, mid+1, right)#右边进行快排递归

@cal_time
def quick_sort(li):
    return _quick_sort(li, 0, len(li)-1)


li = list(range(10000))
# random.shuffle(li)#为防止最坏情况发生，最好先用这局代码完全打乱列表顺序
quick_sort(li)
print(li)

 

快速排序的最坏情况

　　快排的运行时间依赖于划分是否平衡，而平衡与否又依赖于用户划分的主元素。

  • 如果划分是平衡的，那么快速排序算法性能与归并排序一样。
  • 如果划分时不平衡的，那么快速排序的性能就接近于插入排序了

因此，快排的最坏情况的发生与快速排序中主元素的选择是有重大的关系；当主元素是最小元素或最大元素时会使快排性能最差

 

　　堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。

堆的时间复杂度是O(N*logN)，空间复杂度是O(1)，且是一种不稳定的排序方式。

　　在了解堆排序之前我们首先要掌握有关完全二叉树的知识点，二叉树博客地址：http://www.cnblogs.com/zhuminghui/p/8409508.html

　　堆、是一个完全二叉树的数据类型，堆根据数据结构的不同可以分为大根堆和小根堆

大根堆：一棵完全二叉树，满足任一节点都比其孩子节点大

小根堆：一棵完全二叉树，满足任一节点都比其孩子节点小

　　　　　　    　　

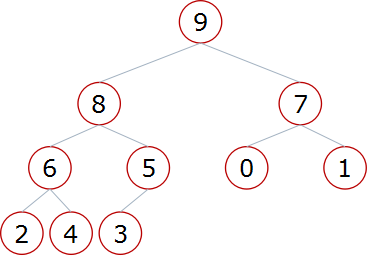
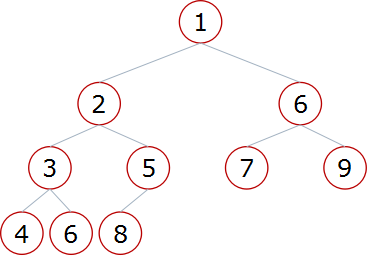
　　　　　　　　　　　　　　大根堆　　　　　　　　　　　　　　　　　　　　　小根堆

 

堆排序的核心就是要构造堆，将数据构造成堆经过以下步骤就可以得到有序的数据：

  1.   建立堆
  2.   得到堆顶元素，为最大元素
  3.   去掉堆顶，将堆最后一个元素放到堆顶，
  4.   此时可通过一次调整重新使堆有序。
  5.   堆顶元素为第二大元素。 重复步骤3，直到堆变空。

假设我们有这样一个数据结构：

　　　　　　　　　　　　　　

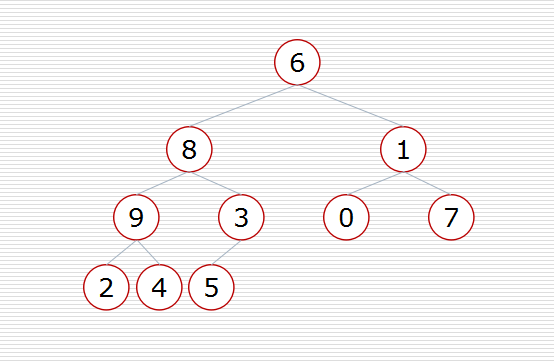
首先我们要构造堆：

　　　　　　　　　　　　

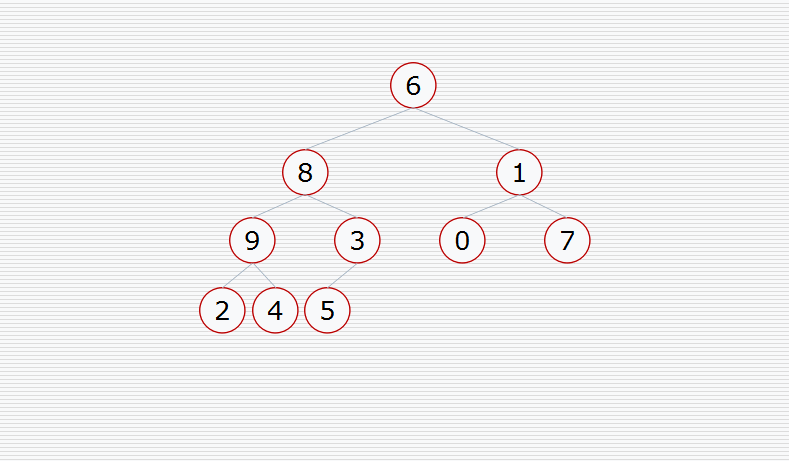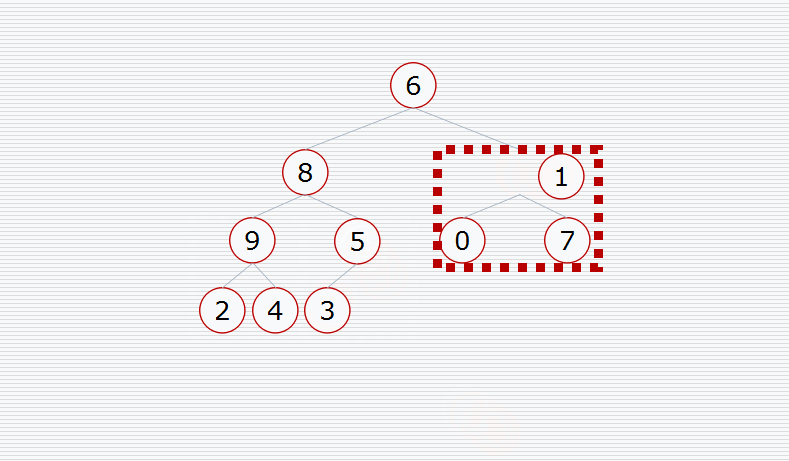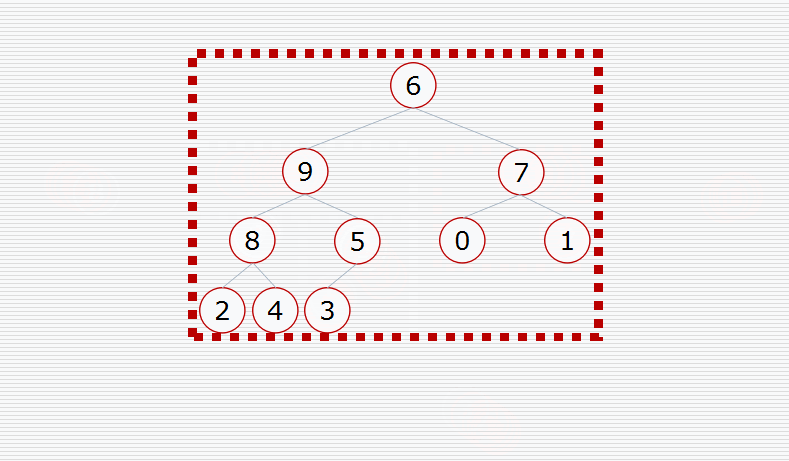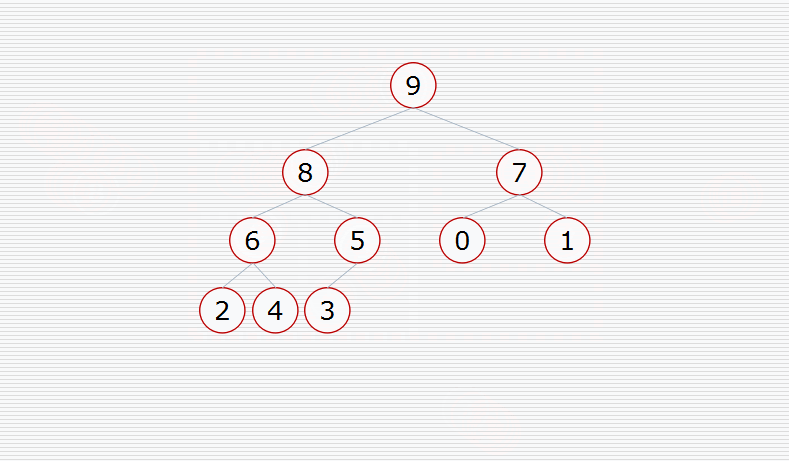
然后挨个出数（注意每次都要构造堆）：

　　　　　　　　　　　　

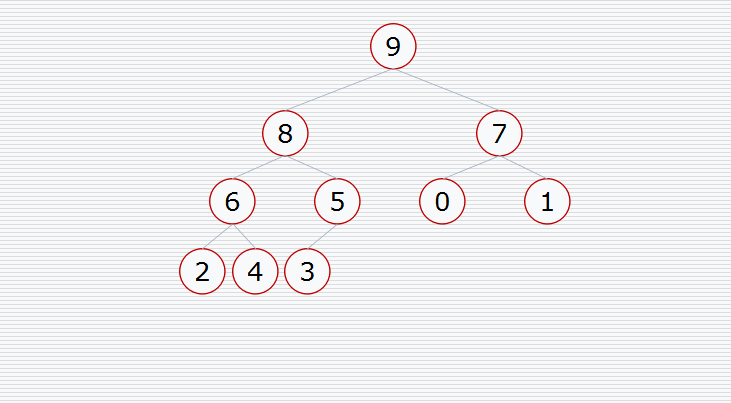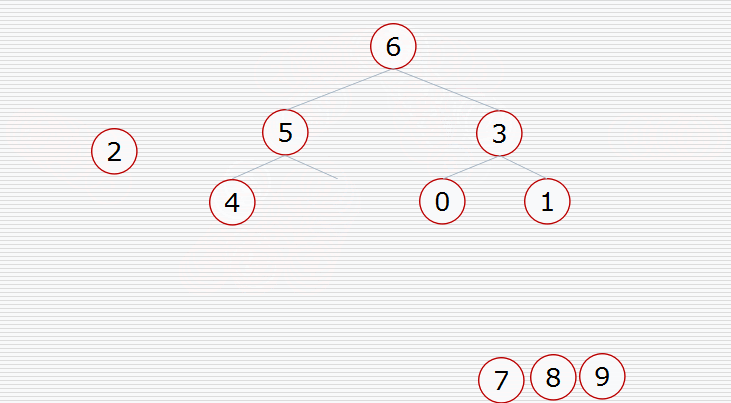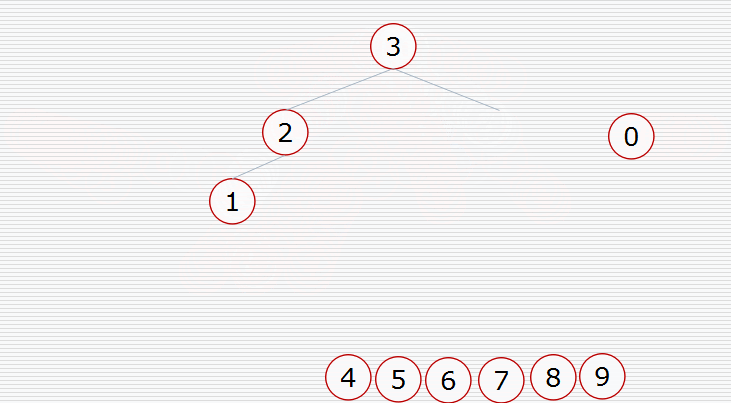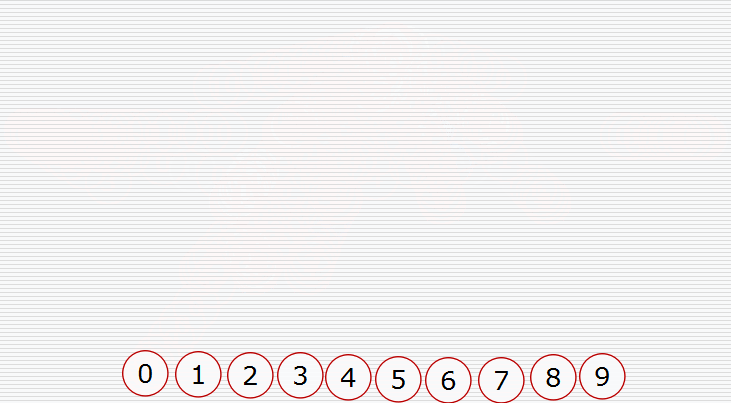
用代码实现：

from timewrap import *
import random

def sift(li, low, high):
    """
    构造堆的过程
    :param li:
    :param low: 堆根节点的位置
    :param high: 堆最后一个节点的位置
    :return:
    """
    i = low         # 父亲的位置
    j = 2 * i + 1   # 孩子的位置
    tmp = li[low]   # 最原来的根的值
    while j <= high:
        if j + 1 <= high and li[j+1] > li[j]: # 如果右孩子存在并且右孩子更大
            j += 1
        if tmp < li[j]: # 如果最原来的根的值比孩子小
            li[i] = li[j]  # 把孩子向上移动一层
            i = j
            j = 2 * i + 1
        else:
            break
    li[i] = tmp# 最原来的根的值放到对应的位置上(叶子节点)

@cal_time
def heap_sort(li):
    n = len(li)
    # 1. 建堆
    for i in range(n//2-1, -1, -1):
        sift(li, i, n-1)
    # 2. 挨个出数
    for j in range(n-1, -1, -1):    # j表示堆最后一个元素的位置
        li[0], li[j] = li[j], li[0]
        # 堆的大小少了一个元素 （j-1）
        sift(li, 0, j-1)


li = list(range(10000))
random.shuffle(li)
heap_sort(li)#heap_sort running time: 0.07304835319519043 secs.
print(li)#0~9999已排好序

 

Python中内置的堆排序模块

　　在Python中堆排序有一个内置模块——heapq模块，利用它我们可以快速实现一个堆排序

import heapq, random

li = [5,8,7,6,1,4,9,3,2]
heapq.heapify(li)#将列表转化为堆
print(li)#[1, 2, 4, 3, 8, 7, 9, 5, 6]
print(heapq.heappop(li))#弹出堆的最小值  1
print(heapq.heappop(li))#弹出堆的最小值  2
heapq.heappush(li,10)#插入一个值 
print(li)#[3, 5, 4, 6, 8, 7, 9, 10]
import heapq, random

def heap_sort(li):
    heapq.heapify(li)
    n = len(li)
    new_li = []
    for i in range(n):
        new_li.append(heapq.heappop(li))
    return new_li

li = list(range(10000))
random.shuffle(li)
li = heap_sort(li)
print(li)#从小到大排序

#内置方法直接一行代码解决问题
print(heapq.nsmallest(100, li))#从小到大排序
print(heapq.nlargest(100, li))#从大到小排序
heapq模块使用方法

 

堆排序例题

　　现在有n个数，设计算法找出前k大的数（k<n）。

思路：取列表前k个元素（假设k=5）建立一个小根堆。堆顶就是目前这k个数中最小的数。 依次向后遍历原列表，对于列表中的元素，如果小于堆顶，则忽略该元素；如果大于堆顶，则将堆顶更换为该元素，并且对堆进行一次调整，使得堆顶永远为目前k个数中的最小数。直到遍历完列表所有元素后，倒序弹出堆顶。

li=[6,8,1,9,3,0,7,2,4,5]
def topk(li,k):
    heap=li[0:k]
    for i in range(k//2-1,-1,-1):
        sift(heap,i,k-1)
    for i in range(k,len(li)):
        if li[i] > heap[0]:
            heap[0]=li[i]
            sift(heap,0,k-1)
    for i in range(k-1,-1,-1):
        heap[0],heap[i]=heap[i],heap[0]
        sift(heap,0,i-1)
View Code

 

　　归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

　　归并过程为：比较a[i]和b[j]的大小，若a[i]≤b[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；否则将第二个有序表中的元素b[j]复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。。

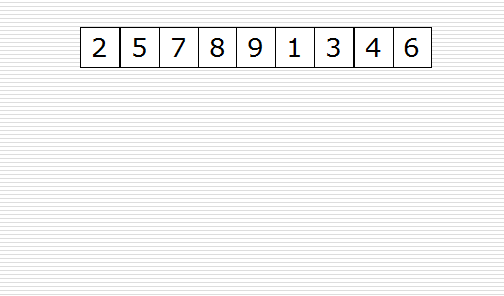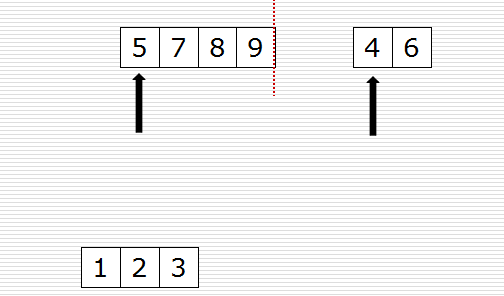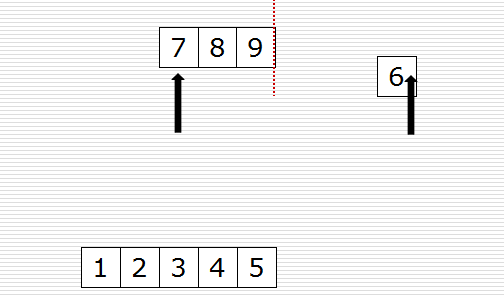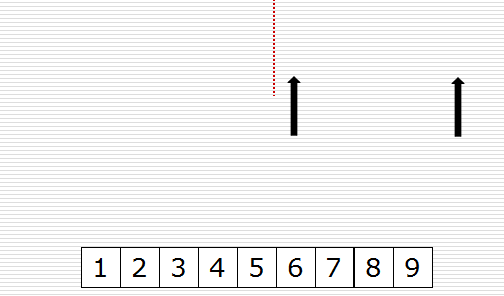
　　时间复杂度为O(nlog₂n) 这是该算法中最好、最坏和平均的时间性能。空间复杂度为 O(n)。归并排序比较占用内存，但却是一种效率高且稳定的算法。

 一次归并的代码如下：

def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:#列表被分为了[low:mid+1],[mid+1:high]两部分
        #分别取两段的小的部分
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:#右取完了段
        ltmp.append(li[i])
        i += 1
    while j <= high:#左段取完了
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp

 

有时列表的复杂度会比较大，这时我们就需要做好几次归并操作才能使得列表有序，这时我们可以用到递归。

基本思路：

　　　　分解：将列表越分越小，直至分成一个元素。

　　　　终止条件：一个元素是有序的。

　　　　合并：将两个有序列表归并，列表越来越大。

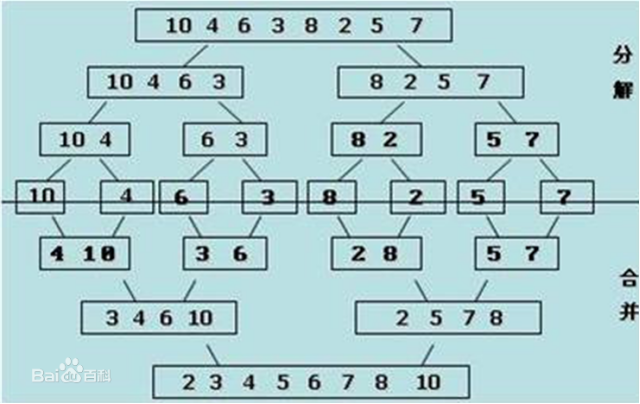
使用递归使得列表有序：

import random
from timewrap import *
import copy
import sys


def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:#列表被分为了[low:mid+1],[mid+1:high]两部分
        #分别取两段的小的部分
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:#右取完了段
        ltmp.append(li[i])
        i += 1
    while j <= high:#左段取完了
        ltmp.append(li[j])
        j += 1
    li[low:high+1] = ltmp


def _merge_sort(li, low, high):
    if low < high:  # 至少两个元素
        mid = (low + high) // 2
        _merge_sort(li, low, mid)
        _merge_sort(li, mid+1, high)
        merge(li, low, mid, high)
        print(li[low:high+1])

@cal_time
def merge_sort(li):
    # 因为函数要进行递归，无法直接安装饰器，所以在外面加个壳。
    # 不使用装饰器的话不用写这个函数，直接用上面的函数就可以
    return _merge_sort(li, 0, len(li)-1)


li = list(range(16))
random.shuffle(li)
merge_sort(li)

print(li)

 

NB 三人组小结 

  • 三种排序算法的时间复杂度都是O(nlogn)
  • 一般情况下，就运行时间而言： 快速排序 < 归并排序 < 堆排序
  • 三种排序算法的缺点：
      • 快速排序：极端情况下排序效率低
      • 归并排序：需要额外的内存开销
      • 堆排序：在快的排序算法中相对较慢

 

前面六种算法的复杂度总结

 

 

 

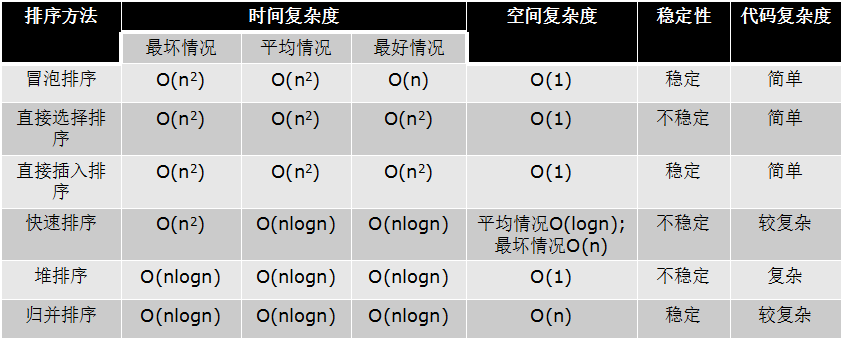
其他排序算法

　　这里补充两个排序算法——希尔排序和计数算法

　　希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”（Diminshing Increment Sort），是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
　　希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。

基本思想：

　　首先取一个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进行直接插入排序； 取第二个整数d2=d1/2，重复上述分组排序过程，直到di=1，即所有元素在同一组内进行直接插入排序。

撸不懂文字的看图：

基本代码实现：

def shell_sort(li):
    d = len(li) // 2#d1
    while d > 0:
        for i in range(d, len(li)):
            tmp = li[i]
            j = i - d#j=1 2 3...
            while li[j] > tmp and j >= 0:
                li[j+d] = li[j]#交换
                j -= d
            li[j+d] = tmp
        d = d >> 1# y>>x 符号表示将y转化成二进制数后砍掉最后x位，效果与 y/= x 一样

 

　　计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。 

　　当然计数排序是一种牺牲空间换取时间的算法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）

计数排序对输入的数据有附加的限制条件：
　　　　1、输入的线性表的元素属于有限偏序集S；
　　　　2、设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。
在这两个条件下，计数排序的复杂性为O(n)。
　　计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

 

 
算法过程：
　　假设输入的线性表L的长度为n，L=L1,L2,..,Ln；线性表的元素属于有限偏序集S，|S|=k且k=O(n)，S={S1,S2,..Sk}；则计数排序可以描述如下：
　　　　1、扫描整个集合S，对每一个Si∈S，找到在线性表L中小于等于Si的元素的个数T(Si)；
　　　　2、扫描整个线性表L，对L中的每一个元素Li，将Li放在输出线性表的第T(Li)个位置上，并将T(Li)减1。

基本代码实现：

import random
from timewrap import *

@cal_time
def count_sort(li, max_num = 100):
    count = [0 for i in range(max_num+1)]#[0,0,0,0,0,0,...]
    for num in li:
        count[num]+=1#li中每有一个元素，就在count中下标为该元素的位置加一，最后得到的就是下标位置（表示li的元素值）是几（表示li中该元素的个数）
    li.clear()#清空li
    for i, val in enumerate(count):
        for _ in range(val):
            li.append(i)#将count中不为0的元素的索引值一个一个加到li中，得到的li就是排好序的li

li = [random.randint(0,100) for i in range(100000)]
count_sort(li)

 

 

 

 

                                                      

 

 

 

 

 

 

 

 

                                     

 

posted @ 2018-02-01 20:27  ''竹先森゜  阅读(4072)  评论(0)  编辑  收藏  举报