PRML读书笔记——Introduction
1.1. Example: Polynomial Curve Fitting
1. Movitate a number of concepts:
(1) linear models: Functions which are linear in the unknow parameters. Polynomail is a linear model. For the Polynomail curve fitting problem, the models is :
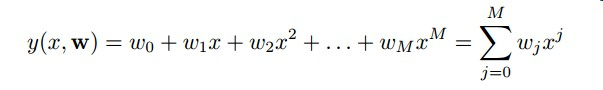
which is a linear model.
(2) error function: error function measures the misfit between the prediction and the training set point. For instance, sum of the squares of the errors is one simple function, which is widely used, and is given:

(3) model comparison or model selection
(4) over-fitting: the model abtains excellent fit to training data and give a very poor performance on test data. And this behavior is known as over-fitting.
(5) regularization: One technique which is often used to control the over-fitting phenomenon, and it involves adding a penalty term to the error function in order to discourage the coefficients from reaching large values. The simplest such penalty term takes the form of a sum of aquares of all of the coefficients, leading to a modified error function of the form:
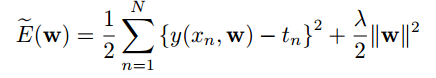
And this particular case of a quadratic regularizer is called ridge regression (Hoerl and Kennard, 1970). In the context of neural networks, this approach is known as weight decay.
(6) validation set, also called a hold-out set: If we were trying to solve a practical application using this approach of minimizing an error function, we would have to find a way to determine a suitable value for the model complexity. a simple way of achieving this, namely by taking the available data and partitioning it into a training set, used to determine the coefficients w, and a separate validation set, also called a hold-out set, used to optimize the model complexity.
1.2. Probability Theory
1. The rules of probability. Sum rule and product rule.

2. Bayes’ theorem.
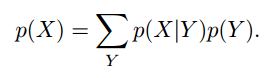

3. Probability densities
4. Expectations and covariances
5. Bayesian probabilities.
Bayes’ theorem was used to convert a prior probability into a posterior probability by incorporating the evidence provided by the observed data.
6. Gaussian distribution
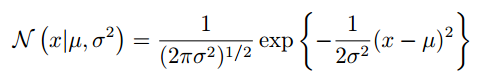

7.maximizing the posterior distribution is equivalent to minimizing the regularized sum-of-squares error function.
1.3. Model Selection
1.6. Information Theory
1 entropy
![]()



