博客作业-图

1.学习总结(2分)

1.1图的思维导图

 

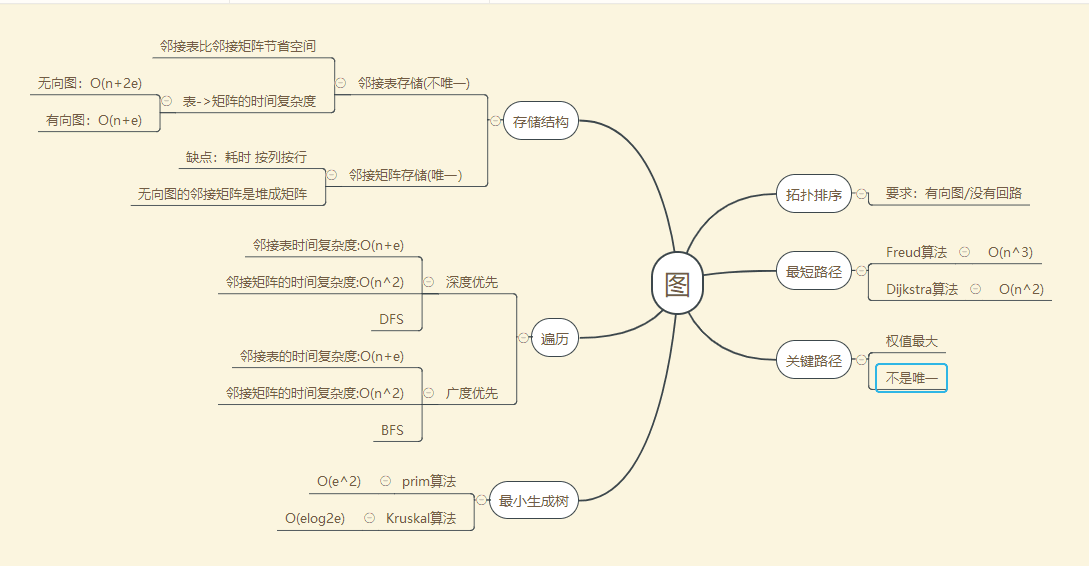
1.2 图结构学习体会

谈谈你对图结构中的几个经典算法学习体会。具体有：

  • 深度遍历算法和广度遍历算法求最小生成树相对而言是比较好理解的，也是图结构中算为简单的方面，但是还没有熟练掌握算法，要加强。
  • Prim和Kruscal算法不论是Kruscal算法还是Prim算法，都是采用了贪心的策略，Kruscal算法是对边集的操作，Prim算法是对点集的操作。
  • Dijkstra算法是典型的单源最短路径算法特点是以起始点为中心向外层层扩展，直到扩展到终点为止。
  • 拓扑排序算法一定为有向图，且一定没有回路。

2.PTA实验作业（4分）

2.1 题目1：图着色问题

2.2 设计思路（伪代码或流程图）

这个问题运用了经典的回溯法将visited数组置0后判断顶点的着色，如果不冲突的话跳出，如果冲突则继续搜索，直到结束。

若顶点全部着色且不冲突，然后输出数组。

当搜索的时候如果着色冲突，是否为合法，否则重置。

2.3 代码截图

 

2.4 PTA提交列表说明。

 

输出答案的格式不对，Y和N 没有大写，

2.1 题目2：排座位

2.2 设计思路（伪代码或流程图）

首先先明确朋友关系为1，敌对关系为-1.那么图的朋友两顶点的权值为1，敌对的两顶的权值为-1.

调用函数判断两个人的关系，如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；如果他们之间并不是朋友，但也不敌对，则输出OK；如果他们之间有敌对，然而也有共同的朋友，则输出OK but...；如果他们之间只有敌对关系，则输出No way。

2.3 代码截图

 

2.4 PTA提交列表说明。

 

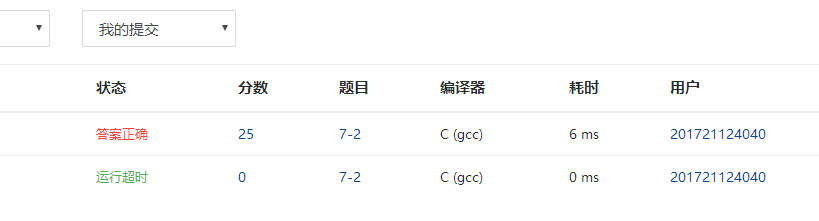
这题的错误点在于没有写好跳出循环的条件导致陷入一个死循环，在不同情况下应该用不同的条件而不是只是小于就可以了。

2.1 题目3：公路村村通

2.2 设计思路（伪代码或流程图）

这个题目顾名思义，即在给出的城镇和公路两者之间，查找是否这些公路能让每个城镇互相同行，并且给出了成本价格，如果可以同行则输出最低成本，即每条公路的最低成本之和。输出成本，如果不行则输出-1表明还需要建设公路。定义函数prime用来判断和计算成本，在函数中用三个循环分别判断，最后返回成本之和。

2.3 代码截图

 

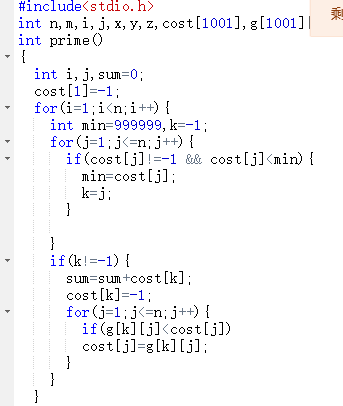
2.4 PTA提交列表说明。

 

这个题目还是没能改全部正确，但是在之前多种错误的情况下是因为错在scanf打错以及main打错导致一直编译不了而且输出格式也错了，

3.截图本周题目集的PTA最后排名（3分）

本次题目集总分：310分

3.1 PTA排名（截图带自己名字的排名）

 

 

3.2 我的总分：180

4. 阅读代码（必做，1分）

我选择了最后一题天梯地图的代码，这个是在CSDN上找的c++代码

其中对于最短时间，要注意取最短的长度的那一条，对于最短距离，要注意取结点个数最少的那一条

  1. #include <iostream>  
  2. #include <string.h>  
  3. #include <stdlib.h>  
  4. #include <stdio.h>  
  5. #include <algorithm>  
  6. #include <math.h>  
  7. #include <string>  
  8. #include <map>  
  9. #include <queue>  
  10. using namespace std;  
  11. const int maxn=1e5;  
  12. struct Node  
  13. {  
  14.     int value;  
  15.     int next;  
  16.     int dis;  
  17.     int time;  
  18. }edge[maxn*4+5];  
  19. int head[maxn+5];  
  20. int tot;  
  21. void join(int x,int y,int d,int t)  
  22. {  
  23.     edge[tot].value=y;  
  24.     edge[tot].next=head[x];  
  25.     edge[tot].dis=d;  
  26.     edge[tot].time=t;  
  27.     head[x]=tot++;  
  28. }  
  29. int vis[maxn+5];  
  30. int ans,res;  
  31. struct node  
  32. {  
  33.     int x;  
  34.     int dis;  
  35.     int num;  
  36.     int time;  
  37.     node(){};  
  38.     node(int x,int dis,int num,int time)  
  39.     {  
  40.         this->x=x;  
  41.         this->dis=dis;  
  42.         this->num=num;  
  43.         this->time=time;  
  44.     }  
  45.     friend bool operator <(node a,node b)  
  46.     {  
  47.         return a.dis>b.dis;  
  48.     }  
  49. };  
  50. int d[maxn+5];  
  51. int d2[maxn+5];  
  52. int num[maxn+5];  
  53. int t[maxn+5];  
  54. int ansd[maxn+5];  
  55. int anst[maxn+5];  
  56. int n;  
  57. int v1,v2;  
  58. void Dijkstra(int v1,int v2)  
  59. {  
  60.     priority_queue<node> q;  
  61.     for(int i=0;i<=n;i++)  
  62.         d[i]=t[i]=1e9;  
  63.     memset(vis,0,sizeof(vis));  
  64.     num[v1]=0;  
  65.     d[v1]=t[v1]=0;  
  66.     ansd[v1]=-1;  
  67.     anst[v1]=-1;  
  68.     while(!q.empty())  
  69.         q.pop();  
  70.     q.push(node(v1,0,0,0));  
  71.     while(!q.empty())  
  72.     {  
  73.         node term=q.top();  
  74.         q.pop();  
  75.         if(term.x==v2)  
  76.         {  
  77.             break;  
  78.         }  
  79.         for(int i=head[term.x];i!=-1;i=edge[i].next)  
  80.         {  
  81.             int v=edge[i].value;  
  82.               
  83.             if(d[v]>term.dis+edge[i].dis)  
  84.             {  
  85.                 d[v]=term.dis+edge[i].dis;  
  86.                 num[v]=term.num+1;  
  87.                 q.push(node(v,d[v],term.num+1,0));  
  88.                 ansd[v]=term.x;  
  89.             }  
  90.             else if(d[v]==term.dis+edge[i].dis)  
  91.             {  
  92.                 if(num[v]>term.num+1)  
  93.                 {  
  94.                     num[v]=term.num+1;  
  95.                     ansd[v]=term.x;  
  96.                     q.push(node(v,d[v],term.num+1,0));  
  97.                 }  
  98.             }  
  99.         }  
  100.     }  
  101.     while(!q.empty())  
  102.         q.pop();  
  103.     q.push(node(v1,0,0,0));  
  104.     d2[v1]=0;  
  105.     while(!q.empty())  
  106.     {  
  107.         node term=q.top();  
  108.         q.pop();  
  109.         if(term.x==v2)  
  110.         {  
  111.             break;  
  112.         }  
  113.         for(int i=head[term.x];i!=-1;i=edge[i].next)  
  114.         {  
  115.             int v=edge[i].value;  
  116.             if(t[v]>term.dis+edge[i].time)  
  117.             {  
  118.                 t[v]=term.dis+edge[i].time;  
  119.                 d2[v]=term.time+edge[i].dis;  
  120.                 q.push(node(v,t[v],0,d2[v]));  
  121.                 anst[v]=term.x;  
  122.             }  
  123.             else if(t[v]==term.dis+edge[i].time)  
  124.             {  
  125.                 if(d2[v]>term.time+edge[i].dis)  
  126.                 {  
  127.                     d2[v]=term.time+edge[i].dis;  
  128.                     q.push(node(v,t[v],0,d2[v]));  
  129.                       
  130.                     anst[v]=term.x;  
  131.                 }  
  132.             }  
  133.         }  
  134.     }  
  135.   
  136.       
  137.       
  138. }  
  139. int fun3(int x)  
  140. {  
  141.     if(x==-1)  
  142.         return 1;  
  143.     if(ansd[x]!=anst[x])  
  144.         return 0;  
  145.     return fun3(ansd[x]);  
  146. }  
  147. void fun(int x)  
  148. {  
  149.     if(x==-1)  
  150.         return;  
  151.     fun(ansd[x]);  
  152.     if(x==v2)  
  153.         printf("%d",x);  
  154.     else  
  155.         printf("%d => ",x);  
  156. }  
  157. void fun2(int x)  
  158. {  
  159.     if(x==-1)  
  160.         return;  
  161.     fun2(anst[x]);  
  162.     if(x==v2)  
  163.         printf("%d",x);  
  164.     else  
  165.         printf("%d => ",x);  
  166. }  
  167. int m,k;  
  168. int main()  
  169. {  
  170.     scanf("%d%d",&n,&m);  
  171.     int x,y,dd,tt,ta;  
  172.     memset(head,-1,sizeof(head));  
  173.     memset(vis,0,sizeof(vis));  
  174.     tot=0;  
  175.     for(int i=1;i<=m;i++)  
  176.     {  
  177.         scanf("%d%d%d%d%d",&x,&y,&ta,&dd,&tt);  
  178.         join(x,y,dd,tt);  
  179.         if(ta==0)  
  180.         join(y,x,dd,tt);  
  181.     }  
  182.     scanf("%d%d",&v1,&v2);  
  183.     Dijkstra(v1, v2);  
  184.     if(fun3(v2)==1)  
  185.     {  
  186.         printf("Time = %d; Distance = %d: ",t[v2],d[v2]);  
  187.         fun2(v2);  
  188.         printf("\n");  
  189.         return 0;  
  190.     }  
  191.     printf("Time = %d: ",t[v2]);  
  192.     fun2(v2);  
  193.     printf("\n");  
  194.     printf("Distance = %d: ",d[v2]);  
  195.     fun(v2);  
  196.     printf("\n");  
  197.       
  198.       
  199.     return 0;  
  200.       
  201. }  
posted @ 2018-06-18 16:40  丑鱼干  阅读(203)  评论(1)  编辑  收藏  举报