图
1.学习总结(2分)
1.1图的思维导图

1.2 图结构学习体会
图是数据结构的一章很重要的内容,属于复杂的非线性数据结构,但无论多么复杂的图都是由顶点和边构成的。图可分为有向图和无向图,图的存储结构有邻接表存储和邻接矩阵存储,邻接表表示不唯一,邻接矩阵表示是唯一的。图的基本运算包括创建图,输出图,遍历图等等。图的其它运算包括图的遍历和生成最小树以及最短路径和拓扑排序,每项内容都有对应的一到两个算法,刚开始学一个两个还好,到后面累计起来就有一定的难度,所以需要我们多花时间去理解和区分这些算法。经过一段时间的学习后,我对图有了一定的了解,发现它还将之前学习的并查集和数组,广义表等内容联系起来,这也就是图的重要性和难点之一。当然,除了一些理论知识外,实践操作也是很重要的,数据结构终归还是需要我们去敲代码,从实际例子中更好的理解算法。而经过PTA的题目后,发现一些原本很复杂的综合应用问题能灵活的运用图来解决,但我本身对于有些题目还是有些不应手,需要借助百度和同学的帮助,但也在这些过程中对图有了更好的理解。相信经过日积月累,一定能把这章内容得心应手的运用。
其中:
- 深度遍历算法:深度遍历算法可以邻接表为存储结构,也可以邻接矩阵为存储结构,二者类似。
- 广度遍历算法:广度遍历算法可以邻接表为存储结构,这时需要一个队列,以类似于层次遍历二叉树的方式遍历图,也可以以邻接矩阵为存储结构。
- Prim和Kruscal算法:Prim和Kruscal算法都是用来构造最小生成树的两种算法,而Prim算法是一种构造性算法,Kruskal算法是一种按权值的递增次序选择合适的边来构造。同时Kruscal可以进行改进,一是将边集排序改为边排序,二是采用并查集。
- Dijkstra算法:该算法是用来求最短路径的算法,需要注意的是此算法不适合含有负权值的带权图求单源最短路径,且一旦某个顶点u添加到S中,则在算法后面的执行中,不会再修改源点v到顶点u的最短路径长度。
- 拓扑排序算法:拓扑排序是指在一个有向图中找一个拓扑排序的过程,对于给定的有向图,采用邻接表作为存储结构,为每个顶点设立一个链表。
2.PTA实验作业(4分)
-
2.1 题目1:图着色问题
-
2.2 设计思路(伪代码或流程图)

2.3 代码截图
-
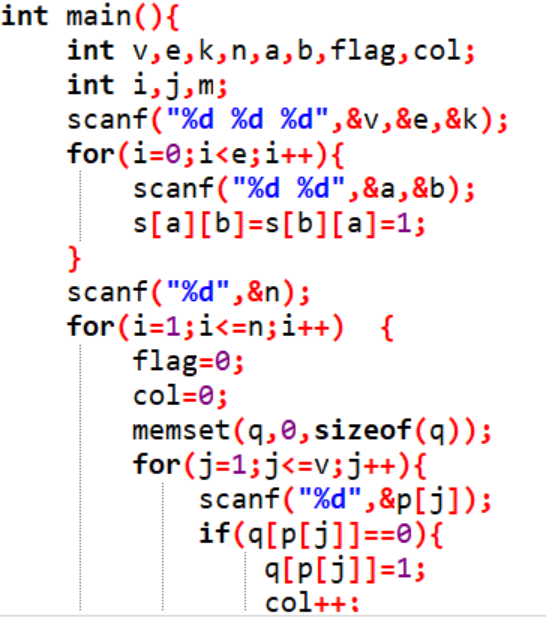
-
2.4 PTA提交列表说明
一开始在只有一分,只对了一个最小图的测试点,在dev上修改了好久都还是这样,后来发现其中一个错误在于每次进入for循环判断的时候没有把数组刷新。修改好之后变成了6分,但还是部分正确。通过提交列表的提示发现部分正确的原因是一些情况的答案错误,也就是在结果的判断代码上出了错误,经过一番观察发现最后方案行不通的情况有两种,一是方案使用的颜色数不是k种,第二种也就是我漏掉的一种是查到了不符合条件的边,加上这种情况后就正确了。
2.1 题目2:排座位
2.2 设计思路
通过“朋友的朋友也是朋友这句话”知道要用并查集完成,由于敌对关系无传递性,要通过一个二位数组存储两两之间的关系,之后通过条件选择判断按要求输出即可。
2.3 代码截图
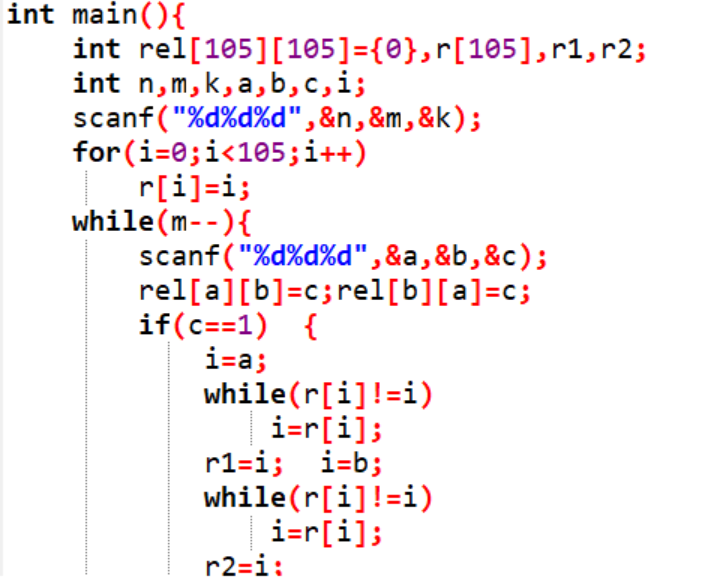


2.4 PTA提交列表说明

这题的题目有好几个弯,对语文的理解能力要求还有点高,一开始用了二维数组来解题无法通过,无奈之下参考了百度才发现要用到之前学过的并查集的知识,因为朋友的朋友也是朋友,说明在一个集合里。但修改后还是无法完全正确,认真推敲之后发现题目中说敌人的敌人不一定是朋友,朋友的敌人也不一定是敌人,所以敌对是有两种情况的,因此就不是用到并查集而是要建立一个环,绕过这好几个弯才把题目解对了。
2.1 题目3:公路村村通
2.2 设计思路
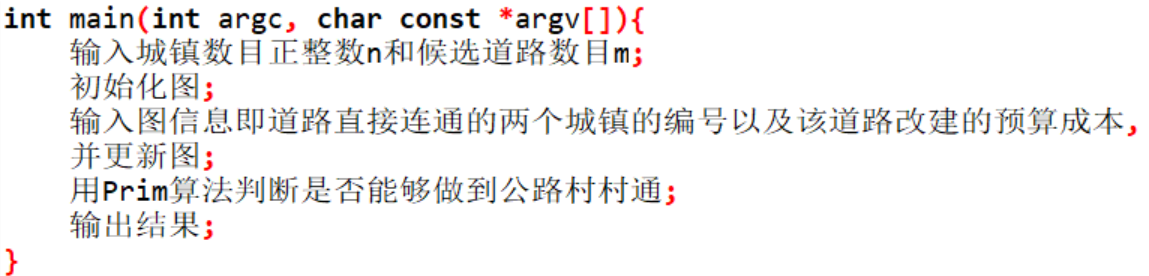
2.3 代码截图
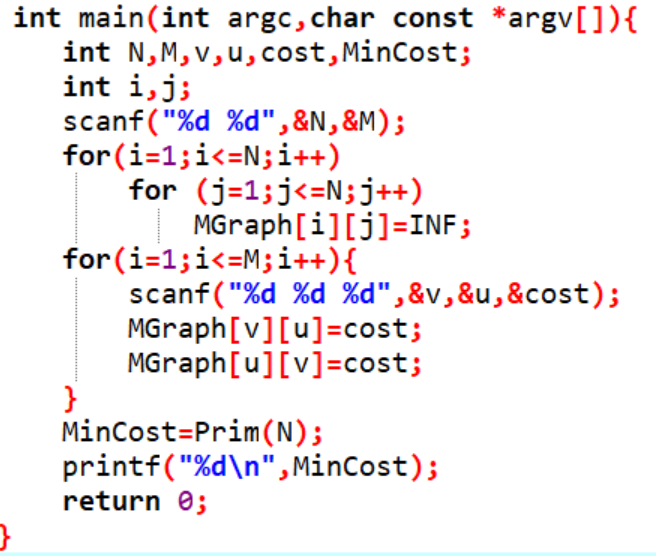
2.4 PTA提交列表说明

这题用Prim算法生成最小生成树,虽然课上对Prim算法有了一定理解,一些选择填空题也能做出来,但到了代码这里还是不能成功,于是向同学询问了思路,一开始部分正确是由于粗心在两个函数的变量定义中,将两个变量用了一个字母表示,从而混乱导致错误,发现问题后修改后就正确了。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:200分:2分
4. 阅读代码:拓扑排序
(1)概念
拓扑排序(Topological Sorting)是一个有向无环图(DAG, Directed Acyclic Graph)的所有顶点的线性序列。且该序列必须满足下面两个条件:1.每个顶点出现且只出现一次。2.若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。有向无环图(DAG)才有拓扑排序,非DAG图没有拓扑排序一说。
(2)应用
通常用来“排序”具有依赖关系的任务。比如,如果用一个DAG图来表示一个工程,其中每个顶点表示工程中的一个任务,用有向边<A,B><A,B>表示在做任务 B 之前必须先完成任务 A。故在这个工程中,任意两个任务要么具有确定的先后关系,要么是没有关系,绝对不存在互相矛盾的关系(即环路)。
(3)实现
根据上面讲的方法,我们关键是要维护一个入度为0的顶点的集合。
图的存储方式有两种:邻接矩阵和邻接表。这里我们采用邻接表来存储图,C++代码如下:
#include<iostream>
#include <list>
#include <queue>
using namespace std;
/************************类声明************************/
class Graph
{
int V; // 顶点个数
list<int> *adj; // 邻接表
queue<int> q; // 维护一个入度为0的顶点的集合
int* indegree; // 记录每个顶点的入度
public:
Graph(int V); // 构造函数
~Graph(); // 析构函数
void addEdge(int v, int w); // 添加边
bool topological_sort(); // 拓扑排序
};
/************************类定义************************/
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
indegree = new int[V]; // 入度全部初始化为0
for(int i=0; i<V; ++i)
indegree[i] = 0;
}
Graph::~Graph()
{
delete [] adj;
delete [] indegree;
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
++indegree[w];
}
bool Graph::topological_sort()
{
for(int i=0; i<V; ++i)
if(indegree[i] == 0)
q.push(i); // 将所有入度为0的顶点入队
int count = 0; // 计数,记录当前已经输出的顶点数
while(!q.empty())
{
int v = q.front(); // 从队列中取出一个顶点
q.pop();
cout << v << " "; // 输出该顶点
++count;
// 将所有v指向的顶点的入度减1,并将入度减为0的顶点入栈
list<int>::iterator beg = adj[v].begin();
for( ; beg!=adj[v].end(); ++beg)
if(!(--indegree[*beg]))
q.push(*beg); // 若入度为0,则入栈
}
if(count < V)
return false; // 没有输出全部顶点,有向图中有回路
else
return true; // 拓扑排序成功
}
