动态规划优化之斜率优化(基础)
原文链接http://www.cnblogs.com/zhouzhendong/p/8697303.html
前置技能
- 知道什么是动态规划,并对一般的动态规划较为了解
- 比较熟悉单调队列,并做过单调队列的题
- 对斜率以及凸包有一定的了解
- 有一定的推式子的能力
斜率优化可能是什么?
顾名思义,就是通过一系列的推导把式子转化成斜率的形式,然后利用一些性质进行优化。
问题模型
有一个长度为$n$的序列$a$,第$i$项元素为$a_i$。保证$a_i$为正整数。
现在请你把这个序列分成若干段。设某一段是从$j$开始$i$结束的,设这个区间的所有的数字的总和为$x$,那么它的花费就是$V=ax^2+bx+c$(这里的a(a>0),b,c会输入,都是常数,别和序列$a$搞混)。
一种划分方式的总花费就是他每一段的花费的和。
问所有划分方式中总花费最小是多少。
$n\leq 5\times 10^6$。
解决方法
首先我们设$dp_i$表示序列前$i$个元素组成的前缀序列的最小总花费。
设
$$sum_i=\sum_{j=1}^{i}a_j$$
我们可以列出DP方程:
$$dp_i=max\{dp_j+a(sum_i-sum_j)^2+b(sum_i-sum_j)+c\} (0\leq j<i)$$
我们假设$j>k$且从$j$转移比从$k$不劣,则:
$$dp_j+a(sum_i-sum_j)^2+b(sum_i-sum_j)+c\leq dp_k+a(sum_i-sum_k)^2+b(sum_i-sum_k)+c$$
$$dp_j+a(sum_i-sum_j)^2+b(sum_i-sum_j)\leq dp_k+a(sum_i-sum_k)^2+b(sum_i-sum_k)$$
$$dp_j+a\cdot sum_i^2-2a\cdot sum_isum_j+a\cdot sum_j^2+b\cdot sum_i-b\cdot sum_j\leq dp_k+a\cdot sum_i^2-2a\cdot sum_isum_k+a\cdot sum_k^2+b\cdot sum_i-b\cdot sum_k$$
$$dp_j-2a\cdot sum_isum_j+a\cdot sum_j^2-b\cdot sum_j\leq dp_k-2a\cdot sum_isum_k+a\cdot sum_k^2-b\cdot sum_k$$
$$(dp_j+a\cdot sum_j^2-b\cdot sum_j)- (dp_k+a\cdot sum_k^2-b\cdot sum_k)\leq 2a\cdot sum_i(sum_j-sum_k)$$
由于$sum$递增,而$j>k$,所以$sum_j-sum_k>0$,所以可以将上式继续转化:
$$\frac{(dp_j+a\cdot sum_j^2-b\cdot sum_j)-(dp_k+a\cdot sum_k^2-b\cdot sum_k)}{sum_j-sum_k}\leq 2a\cdot sum_i$$
我们设
$$x_p=sum_p$$
$$y_p=dp_p+a\cdot sum_p^2-b\cdot sum_p$$
则原不等式可写为:
$$\frac{y_j-y_k}{x_j-x_k}\leq 2a\cdot sum_i$$
于是你会惊奇的发现,$\Large\frac{y_j-y_k}{x_j-x_k}$不就是斜率的式子吗?
设
$$g_{i,j}=\frac{y_i-y_j}{x_i-x_j}$$
则上式可以表示为$g_{j,k}\leq sum_i$
我们来发掘以下$g_{j,k}$的性质。
1. 当$g_{j,k}\leq sum_i$时,由于随着$i$变大,$sum_i$也变大,所以显然从$k$转移是永远不会比$j$好的,所以我们可以把$k$扔掉。
2. 当$g_{i,j}\leq g_{j,k}$时,从$i$或者$k$转移至少有一个不比$j$差,所以可以把$j$扔掉。为什么??
若$g_{i,j}\leq sum_i$,显然$j$要被扔掉,根据第一个性质。
若$g_{i,j}>sum_i$,则$g_{j,k}>sum_i$,那么显然$j$比$k$差,也得被扔掉。
于是我们可以用一个单调队列来维护斜率的单调性。
具体的:
当情况1发生的时候让队首出队。
在进队的时候,如果发生情况2,那么先让队尾出队,然后再进队。
为了避免精度问题,我们可以把$x_i-x_j$乘上来。写成乘积的形式来比大小。
显然每次要选队头的决策最赚。
那么我们再思考一下,既然叫做斜率优化,那么显然有一些关于斜率的性质。
我们如果把上述的决策放到单调队列里,然后再平面直角坐标系中描出这些点,并依次相连,会得到一个这样的图:
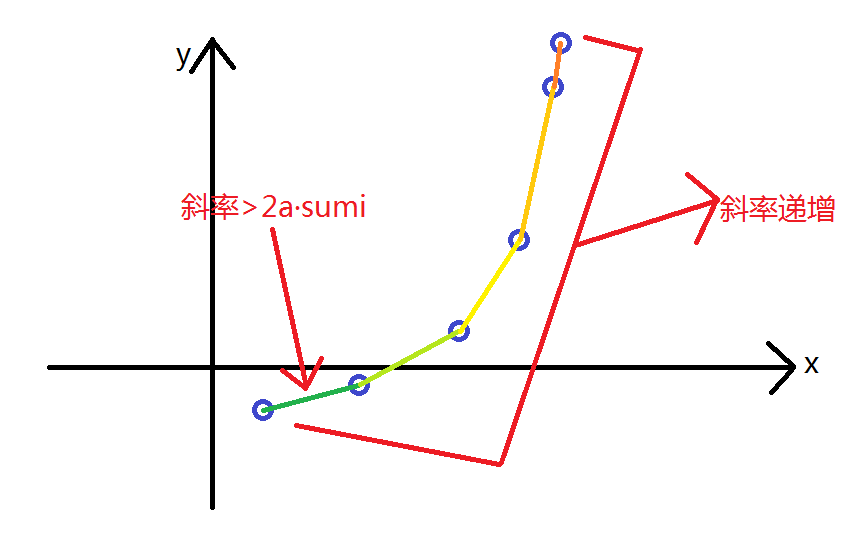
然后你会发现这个右下角是个凸包的一部分。我们叫他下凸壳。
然后你就和凸包联系起来了。
由于博主见识短浅,所以不再进行凸包性质的拓展。
读者可以自己科普。
例子就这么快的讲完了,请读者好好回顾,务必理解。
我直接开始放例题了。
例题
以下例题链接是较为详细的题解(点击题号即可进入)。题解上部有题目链接。
题意
把一个整数序列划分成任意连续的段,使得划分出来的每一段的价值和最大。对于某一段,价值的计算公式为 $V=ax^2+bx+c$,其中 $x$ 为当前段的数值和。
$1\leq n\leq 1000000,-5\leq a\leq -1,|b|\leq 10000000,|c|\leq 10000000,1\leq xi\leq 100$
提示
注意这题和例题非常相似,但是注意一个很大的不同!这里的$a$为负数。所以很多不等式符号都要取相反方向。
题意
有N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3x5的地和一块5x3的地,则他需要付5x5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
提示
考虑到如果长方形A的长和款都比B小,那么A就可以附着在B里面买,而且不加花费,所以这些可以删掉,是没用的。
本题由于是我很久以前做的,题解没有用Latex,所以特别丑,请别介意。
请注意两块相同土地的情况,别全都删光。
然后把土地按照长升序排列,得到的土地的宽必然是降序的,所以就可以很快写出DP方程并斜率优化了。
题意
划分序列,每一段的花费为$(i-j+(\sum_{k=i}^j C_k)-L)^2$,问最小花费。序列长度$\leq 5\times 10^4$。
提示
DP方程应该很好写吧。
手工展开式子得到关于$i$的二次项,关于$j$的二次项,以及$k\cdot ij$这种形式。
根据斜率优化的套路,把只含$i$的左右消掉,把含$i,j$或者$i,k$的移向同一侧,然后除过来。
题意
长为$n$的序列$A$划分,设某一段为$[i,j]$,则其花费为$A_j+\sum_{k=i}^{j}(j-k)$。最小化总花费。$n\leq 10^6$。
提示
同样也是化开,再按照斜率优化的套路来。
为了避免精度问题,我们可以通过把$x,y$同时乘上一个常数来除去分母对精度的影响。
题意
每一段的花费为$a_i+\sum_{k=j+1}^{i}(i-k)b_k$.最小化总花费。$n\leq 10^6$。
提示
考虑预处理带权前缀和$vsum_i=\sum_{j=1}^{i}(j\cdot b_j)$。
题意
每一段的花费为$a_i+\sum_{k=j+1}^{i}(X_i-X_k)b_k$.最小化总花费。$n\leq 10^6$。
提示
上一题的一个小小的升级版。
考虑把预处理的带权前缀和改为$vsum_i=\sum_{j=1}^{i}(X_jb_j)$。
题意
对于一个非负整数序列,小H需要重复k次以下的步骤:
1.选择一个长度超过1的序列
2.从任意位置将序列分割成两个非空的新序列。
每次,小H将会得到分数。分数为两个新序列中元素和的乘积。请选择一种最佳的分割方式,使得k轮之后,使总得分最大。输出总得分。
$n\leq 10^5,k\leq min(n-1,200)$
提示
这题比较不错。
首先证明一个性质:对于一个最终的划分方案,以各种不同顺序划分,所得到的得分总是相同。
然后$dp_{r,i}$表示划分到前$i$个,划分了$r$轮的最大总得分。然后斜率优化。
注意空间限制较紧,要滚动。
题意
有一个N个点的环,相邻两个点距离是1。点顺时针标号为1..N。最初每一个点是空的。要求最终点i存在ri头牛。你有∑ri头牛。你可以选择最多k个点,然后把你的牛任意分配在这k个点里。之后,每一头牛可以选择不动,也可以顺时针走d格并呆在那里。这样,它要耗费d的能量。通过合理选择点、合理分配牛、合理安排牛的走动,使得消耗的总能量最小。
$n\leq 1000,k\leq 7,r_i\leq 10^6$
提示
先证明一个小小的性质。
然后断环为链,并参照BZOJ3675以及BZOJ1096的做法。
注意初始化$dp_{0,i}$为$\infty$。


