BZOJ3560 DZY Loves Math V 数论 快速幂
原文链接http://www.cnblogs.com/zhouzhendong/p/8111725.html
UPD(2018-03-26):蒟蒻回来重新学数论了。更新了题解和代码。之前的怼到后面去了。
题目传送门 - BZOJ3560
题意概括
给定$n$个正整数$a_1,a_2,a_3,...,a_n$,求
$$\Huge\sum_{i_1|a_1}\sum_{i_2|a_2}\cdots \sum_{i_n|a_n}\varphi(i_1i_2i_3...i_n)$$
答案对$10^9+7$取模。
$1\leq n\leq 10^5,1\leq a_i\leq 10^7$
题解
考虑到$\varphi$是积性函数,所以我们可以对于每一个质数分别考虑。
对于每一个质数,考虑它有哪些情况,同一个质数的所有情况贡献加起来,然后不同质数的答案乘起来就OKla。
考虑对一个质数的处理。
先处理出每一个$a_i$含有该质因子几个(假设有$t_i$个)。保存好。
我们显然不可能穷举所有情况。我们考虑采用不同的$a_i$分开贡献的方式。
由于(p为质数)$f(p)=p-1,f(p^i)=f(p^{i-1})*p$,于是一开始的那个$f(p)=p-1$就特别令人不爽!!
于是我们暂且假装$f(p)=p$。这样的话,数$a_i$的贡献就是$\sum_{j=0}^{t_i}f(p^j)$。
于是算出来的当前质数的总贡献就是$\prod_{i=1}^{n}\sum_{j=0}^{t_i}f(p^j)$。
那个$\sum_{j=0}^{k}f(p^j)$可以预处理。
但是别忘了这个是个假贡献。我们假装了$f(p)=p$,事实上不是。
我们考虑还原。
该贡献可以分成两个部分:
1.$\prod_{j=1}^{n}i_j$中不含该质数因子,贡献为1。
2.包含,贡献比标准多了$\frac{1}{p-1}$。
于是搞个逆元还原一下2的部分就可以得到正确答案了。
具体实现大概我知道的有2种方式。
设$m=max\{a_i,i\in[1,n]\}$。
一种是我之前抄的做法:先分解n个数,然后按照质因子排序分段处理。时间复杂度$O(n \sqrt m +n log\ m)$。
一种是我这次写的做法:先筛法把小于$\sqrt m$的素数筛出来,然后对于每一个因子枚举n个数统计相关信息。对于大于$\sqrt m$的质因数用map存下来。最后一个一个算质数贡献。复杂度相同。常数貌似变小了。(BZOJ上快了近4倍)
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+5,M=1e7+5,mod=1e9+7;
int prime[N],pcnt,ptot[N][30];
bool f[M];
map <int,int> hptot;
void get_prime(){
pcnt=0;
memset(f,true,sizeof f);
f[0]=f[1]=0;
for (int i=2;i*i<M;i++){
if (!f[i])
continue;
prime[++pcnt]=i;
for (int j=1;j<=i;j++)
f[i*j]=0;
}
}
LL Pow(LL x,LL y){
if (!y)
return 1LL;
LL xx=Pow(x,y/2);
xx=xx*xx%mod;
if (y&1LL)
xx=xx*x%mod;
return xx;
}
LL Inv(LL x){
return Pow(x,mod-2);
}
int n,a[N],v[N],cntv=0;
int main(){
get_prime();
scanf("%d",&n);
for (int i=1;i<=n;i++)
scanf("%d",&a[i]);
memset(ptot,0,sizeof ptot);
hptot.clear();
for (int i=1;i<=pcnt;i++)
for (int j=1;j<=n;j++){
int k=0;
while (a[j]%prime[i]==0)
a[j]/=prime[i],k++;
ptot[i][k]++;
}
for (int i=1;i<=n;i++)
if (a[i]>1){
if (hptot[a[i]]==0)
v[++cntv]=a[i];
hptot[a[i]]++;
}
LL ans=1;
for (int i=1;i<=pcnt;i++){
LL phi=prime[i]+1,add=1;
for (int j=1;j<30;j++){
while (ptot[i][j]--)
add=add*phi%mod;
phi=(phi*prime[i]+1)%mod;
}
ans=ans*((add-1+mod)%mod*Inv(prime[i])%mod*(prime[i]-1)%mod+1)%mod;
}
for (int i=1;i<=cntv;i++){
LL phi=v[i]+1,add=1;
while (hptot[v[i]]--)
add=add*phi%mod;
ans=ans*((add-1+mod)%mod*Inv(v[i])%mod*(v[i]-1)%mod+1)%mod;
}
printf("%lld",ans);
return 0;
}
——————Old——————
题意概括
给定n个正整数a1,a2,…,an,求
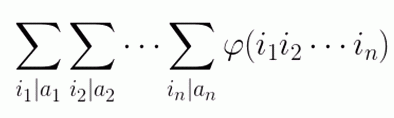
的值(答案模10^9+7)。
1<=n<=10^5,1<=ai<=10^7。
题解
本人是蒟蒻。
可以看这位大佬的(给出链接)
http://blog.csdn.net/popoqqq/article/details/42739963
代码
呵呵,调试的时候照着他的改,改的几乎一样……
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long LL;
const LL N=100005;
LL mod=1e9+7;
LL n,tot=0;
struct Node{
LL p,t;
}q[N*20];
bool operator < (Node a,Node b){
return a.p<b.p;
}
void fj(LL v){
for (LL i=2;i*i<=v;i++)
if (v%i==0){
q[++tot].p=i;
q[tot].t=0;
while (v%i==0)
v/=i,q[tot].t++;
}
if (v>1)
q[++tot].p=v,q[tot].t=1;
}
LL Pow(LL x,LL y,LL mod){
if (y==0)
return 1LL;
LL xx=Pow(x,y/2,mod);
xx=xx*xx%mod;
if (y&1LL)
xx=xx*x%mod;
return xx;
}
LL Inv(LL x,LL mod){
return Pow(x,mod-2,mod);
}
LL calc(LL L,LL R){
LL sum[30];
LL p=q[L].p,res=1;
sum[0]=1;
for (int i=1;i<30;i++)
sum[i]=(sum[i-1]*p+1)%mod;
for (int i=L;i<=R;i++)
res=res*sum[q[i].t]%mod;
res=(res-1)*(p-1)%mod*Inv(p,mod)%mod+1;
return res%mod;
}
int main(){
scanf("%lld",&n);
for (int i=1,a;i<=n;i++){
scanf("%lld",&a);
fj(a);
}
sort(q+1,q+tot+1);
int last=0;
LL ans=1;
for (int i=1;i<=tot;i++)
if (i==tot||q[i].p!=q[i+1].p)
ans=ans*calc(last+1,i)%mod,last=i;
printf("%lld",(ans%mod+mod)%mod);
return 0;
}


