BZOJ1845 [Cqoi2005] 三角形面积并 扫描线 计算几何
欢迎访问~原文出处——博客园-zhouzhendong
去博客园看该题解
题目传送门 - BZOJ1845
题意概括
给出n个三角形,求其面积并。
题解
有一个很经典的扫描线题目:矩形面积并。那个比较简单,建议先去看看 —— 传送门 - 矩形面积并。
这个扫描线的算法,我之前就看过。
之前想了想,还以为是n4logn的,自己以为理解错了,所以就弃坑了一段时间。
现在再想想,原来之前思考的是对的,只是复杂度想错了。其实是n3logn的。
我们按照Y来排序,同样的,我们来看一组图片。

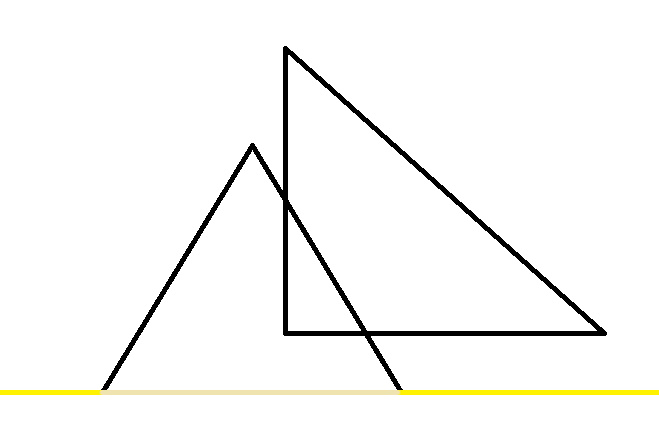

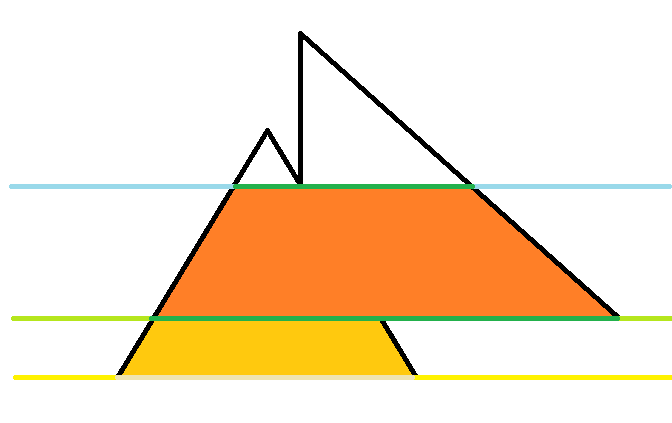

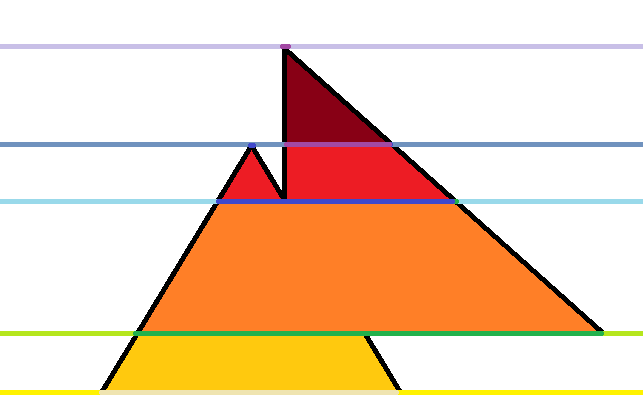
然后大概你已经深有感触了。
步骤:把所有的分成多个梯形,然后扫描线解决。
在这之前,我们需要把所有的交点都求出来。
当然,对于上例第一层和第二层的情况十分坑。第二条扫描线的有效长度不仅和其本身的参数有关,还和该边放在上面还是下面有关。
最后,诡异的是,ans要减去Eps才可以A掉。当然也有大佬不减的Orz,题目卡精度啊!
做个好人,代码后面一组数据。
代码
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long double LD;
const int N=300+5;
const LD Eps=1e-8,Inf=1e9;
int Dcmp(LD x){
if (fabs(x)<Eps)
return 0;
return x<0?-1:1;
}
struct Point{
LD x,y;
Point (){}
Point (LD x_,LD y_){
x=x_,y=y_;
}
Point operator + (Point a){
return Point(x+a.x,y+a.y);
}
Point operator - (Point a){
return Point(x-a.x,y-a.y);
}
Point operator * (LD a){
return Point(x*a,y*a);
}
Point operator / (LD a){
return Point(x/a,y/a);
}
bool operator == (Point a){
return !Dcmp(x-a.x)&&!Dcmp(y-a.y);
}
void read(){
scanf("%Lf%Lf",&x,&y);
}
};
LD Dot(Point a,Point b){
return a.x*b.x+a.y*b.y;
}
LD Cross(Point a,Point b){
return a.x*b.y-a.y*b.x;
}
LD Cross(Point a,Point b,Point c){
return Cross(b-a,c-a);
}
struct Line{
Point a,b;
Line (){}
Line (Point a_,Point b_){
a=a_,b=b_;
}
Line Mat(){
return Line(Point(min(a.x,b.x),min(a.y,b.y)),Point(max(a.x,b.x),max(a.y,b.y)));
}
};
LD Length(Line a){
return sqrt(Dot(a.a-a.b,a.a-a.b));
}
Point Cut_Point(Line L,LD y){
Point a=L.a,b=L.b;
LD da=y-a.y,dy=b.y-a.y,dx=b.x-a.x;
if (!Dcmp(dy))
return Point(Inf,Inf);
return Point(a.x+dx/dy*da,y);
}
Line OrderedY_Line(Point a,Point b){
if (Dcmp(a.x-b.x)>0)
swap(a,b);
return Line(a,b);
}
bool cmp_x(Point a,Point b){
return Dcmp(a.x-b.x)<0;
}
bool cmp_y(Point a,Point b){
return Dcmp(a.y-b.y)<0;
}
struct Triangle{
Point P[3];
Line L[3];
void build(Point x,Point y,Point z){
P[0]=x,P[1]=y,P[2]=z;
L[0]=Line(x,y),L[1]=Line(x,z),L[2]=Line(y,z);
}
Line Cut(int type,LD Y,bool &flag){
flag=1;
Point P_[3];
for (int i=0;i<3;i++)
P_[i]=P[i];
sort(P_,P_+3,cmp_y);
if (Dcmp(P_[1].y-Y)==0&&Dcmp(P_[2].y-Y)==0)
swap(P_[0],P_[2]);
if (Dcmp(P_[0].y-Y)==0&&Dcmp(P_[1].y-Y)==0){
if (type==0){
if (Dcmp(P_[2].y-Y)<0){
flag=0;
return Line(Point(Inf,Inf),Point(Inf,Inf));
}
return OrderedY_Line(P_[0],P_[1]);
}
else {
if (Dcmp(P_[2].y-Y)>0){
flag=0;
return Line(Point(Inf,Inf),Point(Inf,Inf));
}
return OrderedY_Line(P_[0],P_[1]);
}
}
Point p[3];
Line M[3];
for (int i=0;i<3;i++){
p[i]=Cut_Point(L[i],Y);
M[i]=L[i].Mat();
}
if (Dcmp(Y-min(M[0].a.y,M[1].a.y))<0||Dcmp(Y-max(M[0].b.y,M[1].b.y))>0){
flag=0;
return Line(Point(Inf,Inf),Point(Inf,Inf));
}
for (int i=0;i<3;i++)
if (Dcmp(Y-M[i].a.y)<0||Dcmp(Y-M[i].b.y)>0)
return OrderedY_Line(p[(i+1)%3],p[(i+2)%3]);
sort(p,p+3,cmp_x);
return OrderedY_Line(p[0],p[0]==p[1]?p[2]:p[1]);
}
};
bool Crossed(Line a,Line b){
return Dcmp(Cross(a.a,a.b,b.a))*Dcmp(Cross(a.a,a.b,b.b))<0&&Dcmp(Cross(b.a,b.b,a.a))*Dcmp(Cross(b.a,b.b,a.b))<0;
}
Point Cross_Point(Line a,Line b){
Point P=a.a,Q=b.a,v=a.b-a.a,w=b.b-b.a,u=P-Q;
LD t=Cross(w,u)/Cross(v,w);
return P+v*t;
}
int n,m;
Triangle Tri[N];
LD Y[N*N];
bool cmp_Lx(Line a,Line b){
return Dcmp(a.a.x-b.a.x)<0;
}
LD GetLen(int type,int pos_Y){
LD y=Y[pos_Y];
Line L[N];
int tot=0;
for (int i=1;i<=n;i++){
bool flag;
L[++tot]=Tri[i].Cut(type,y,flag);
if (!flag)
tot--;
}
if (tot==0)
return 0;
sort(L+1,L+tot+1,cmp_Lx);
LD ans=L[1].b.x-L[1].a.x,max_x=L[1].b.x;
for (int i=2;i<=tot;i++){
max_x=max(max_x,L[i].a.x);
if (Dcmp(max_x-L[i].b.x)>0)
continue;
ans+=L[i].b.x-max_x;
max_x=max(max_x,L[i].b.x);
}
return ans;
}
int main(){
scanf("%d",&n);
for (int i=1;i<=n;i++){
Point x,y,z;
x.read(),y.read(),z.read();
Tri[i].build(x,y,z);
}
m=0;
for (int i=1;i<=n;i++)
for (int j=i+1;j<=n;j++)
for (int u=0;u<3;u++)
for (int v=0;v<3;v++)
if (Crossed(Tri[i].L[u],Tri[j].L[v]))
Y[++m]=Cross_Point(Tri[i].L[u],Tri[j].L[v]).y;
for (int i=1;i<=n;i++)
for (int j=0;j<3;j++)
Y[++m]=Tri[i].P[j].y;
sort(Y+1,Y+m+1);
LD ans=0,pre=GetLen(0,1);
for (int i=2;i<=m;i++){
if (Dcmp(Y[i]-Y[i-1])==0)
continue;
ans+=0.5*(pre+GetLen(1,i))*(Y[i]-Y[i-1]);
pre=GetLen(0,i);
}
printf("%.2Lf",ans-Eps);
return 0;
}
数据
2
0 0 2 0 0 3
2 0 0 2 3 2
ans=5.33
数据解释: