POJ1151Atlantis 矩形面积并 扫描线 线段树

欢迎访问~原文出处——博客园-zhouzhendong

去博客园看该题解

---

题目传送门 - POJ1151

---

题意概括

　　给出n个矩形，求他们的面积并。

　　n<=100

---

 

题解

　　数据范围极小。

　　我们分3种算法逐步优化。

 

　　算法1： O(n³)

　　如果这n个矩形的坐标都是整数，而且比较小，那么我们显然可以用最暴力的方法：一个一个打标记。

　　但是不是这样的。

　　坐标大小很大，而且是实数。

　　然而我们发现差不多，只要先离散化一下，然后再打标记即可。

 

　　算法2：O(n²)

　　实际上，上面的方法十分慢。如果n的范围到了1000，上面的就无济于事了。

　　而实际上，基于上面的打标记的算法，我们可以通过差分的方法n²解决。

　　我们通过差分，可以用n²的时间标记，n²的时间判断每一个区域是否被覆盖。

　　空间复杂度O(n²)

 

　　算法3：O(n logn) 扫描线

　　实际上，这类问题的数据范围可以到100000这个级别。

　　矩形面积并可以用扫描线算法来解决。先看原理，后面讲具体实现。

　　比如下图：

　　

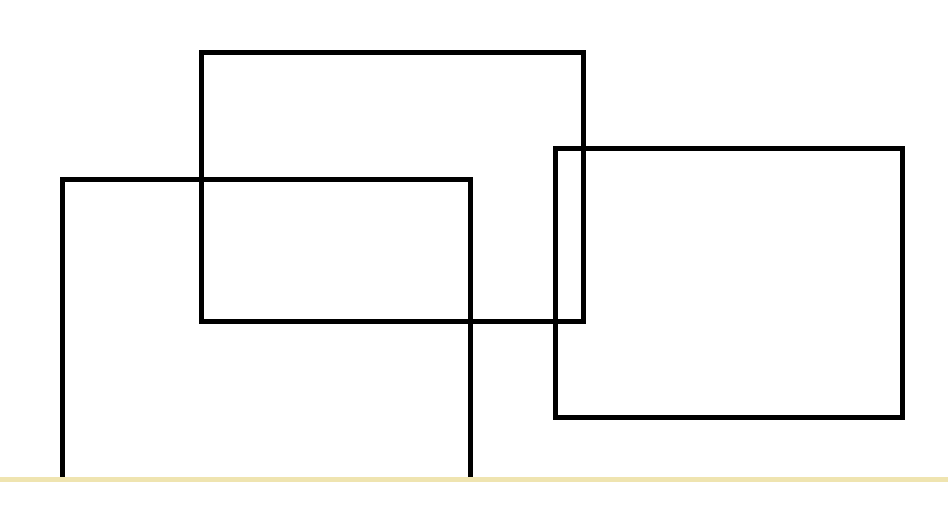
　　当前我们的扫描线到达了淡黄色部分。

　　由于之前没有记录，所以答案不增加。

　　然而我们记下当前横向覆盖的长度。

　　然后我们到了第二条扫描线，加上原来记录的横向覆盖长度乘以增加的高度就是当前增加的答案。

　　然后，我们更新了横向覆盖的长度。

　　继续。

　　

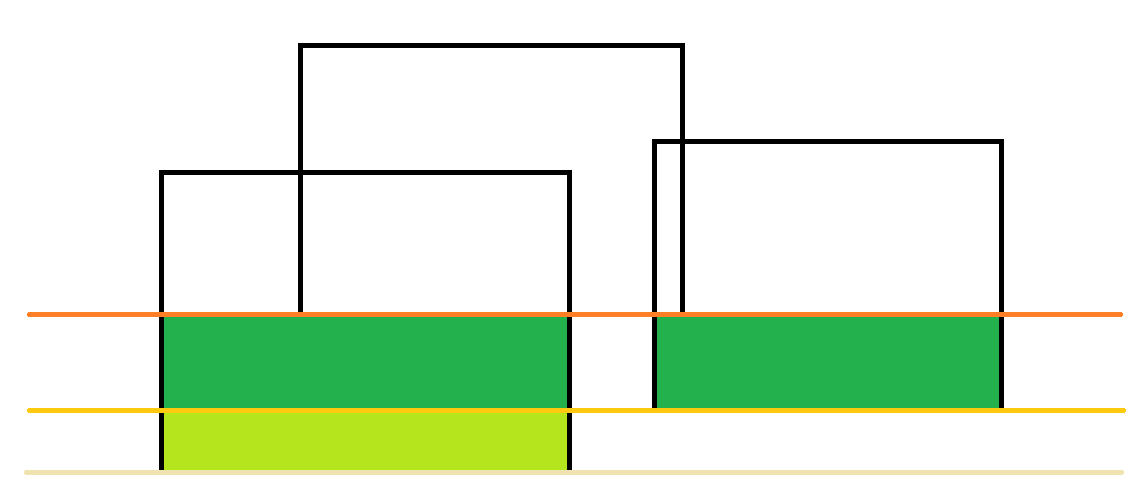
　　然后第三条。现在的横向覆盖长度是两边加起来，所以增加的面积是两块了。

　　然后更新横向覆盖的长度，加上了中间的那一条。

　　然后继续。

　　

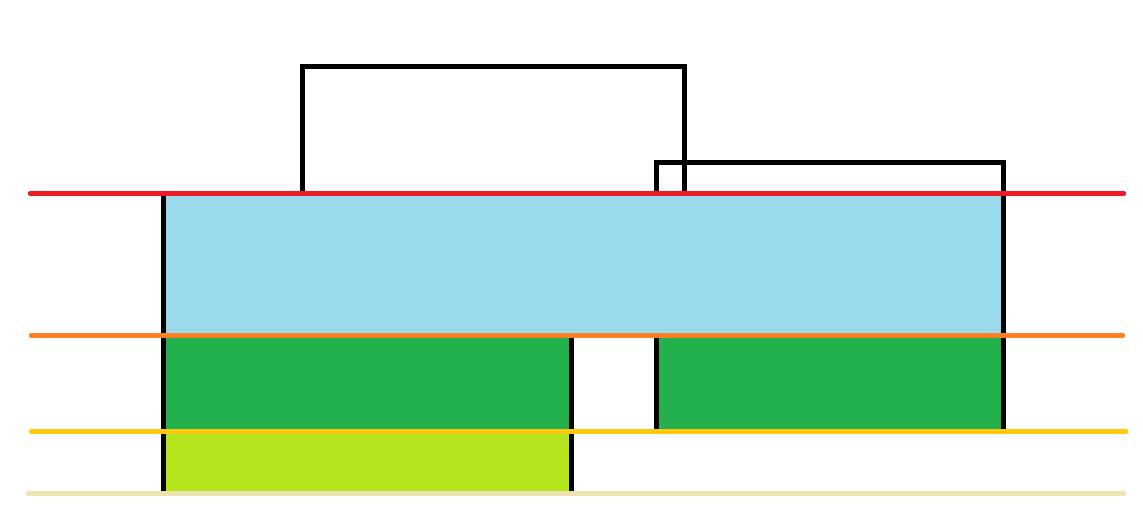
　　现在有这么长的一条都是被横向覆盖的了。

　　所以新增的面积是浅蓝色部分。

　　然后我们发现左上那条线是出边，所以要删除这一条线。

　　所以横向覆盖的长度为如下：

　　

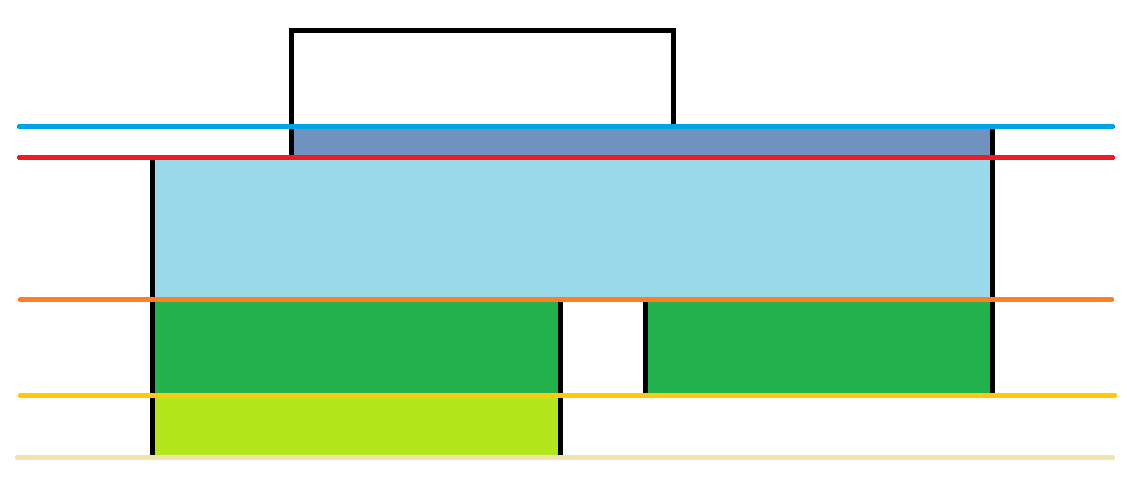
　　同理，接下来是：

　　

　　然后就OK了。

　　

　　那么具体怎么实现呢？

　　我们开一棵线段树来维护！

　　在读入之后，我们把所有的横线都拆开，分成下边和上边两类。某一区间在进入下边的时候+1，离开上边的时候-1，所以我们分别给上下边标记+1和-1。

　　对于Y，我们离散化一下。

　　对于X，我们按照边的X排一个序。

　　然后按照刚才那样的处理。

　　具体如何维护详见代码。

---

 

代码

#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
const int N=100+5,M=N*2;
const double Eps=1e-9;
int T=0,n,m,tot_Y,tot_s;
double Y[M];
struct Segment{
    double x,L,R;
    int v;
    void set(double x_,double L_,double R_,int v_){
        x=x_,L=L_,R=R_,v=v_;
    }
}s[M];
struct SegTree{
    int cnt;
    double sum;
}t[M*4];
bool cmp_s(Segment a,Segment b){
    return a.x<b.x;
}
void build(int rt,int le,int ri){
    t[rt].cnt=0;
    t[rt].sum=0;
    if (le==ri)
        return;
    int mid=(le+ri)>>1,ls=rt<<1,rs=ls|1;
    build(ls,le,mid);
    build(rs,mid+1,ri);
}
void pushup(int rt,int le,int ri){
    int ls=rt<<1,rs=ls|1;
    if (t[rt].cnt)
        t[rt].sum=Y[ri+1]-Y[le];
    else if (le==ri)
        t[rt].sum=0;
    else
        t[rt].sum=t[ls].sum+t[rs].sum;
}
void update(int rt,int le,int ri,int xle,int xri,int d){
    if (le>xri||ri<xle)
        return;
    if (xle<=le&&ri<=xri){
        t[rt].cnt+=d;
        pushup(rt,le,ri);
        return;
    }
    int mid=(le+ri)>>1,ls=rt<<1,rs=ls|1;
    update(ls,le,mid,xle,xri,d);
    update(rs,mid+1,ri,xle,xri,d);
    pushup(rt,le,ri);
}
int find_double(double x){
    int le=1,ri=m,mid;
    while (le<=ri){
        mid=(le+ri)>>1;
        if (abs(x-Y[mid])<Eps)
            return mid;
        if (Y[mid]<x)
            le=mid+1;
        else
            ri=mid-1;
    }
}
int main(){
    while (scanf("%d",&n)&&n){
        tot_Y=tot_s=0;
        for (int i=1;i<=n;i++){
            double xA,yA,xB,yB;
            scanf("%lf%lf%lf%lf",&xA,&yA,&xB,&yB);
            if (yB-yA<Eps||xB-xA<Eps)
                continue;
            Y[++tot_Y]=yA,Y[++tot_Y]=yB;
            s[++tot_s].set(xA,yA,yB,1);
            s[++tot_s].set(xB,yA,yB,-1);
        }
        sort(Y+1,Y+tot_Y+1);
        sort(s+1,s+tot_s+1,cmp_s);
        m=1;
        for (int i=2;i<=tot_Y;i++)
            if (Y[i]-Y[i-1]>Eps)
                Y[++m]=Y[i];
        build(1,1,m);
        double ans=0;
        for (int i=1;i<=tot_s;i++){
            ans=ans+(s[i].x-s[i-1].x)*t[1].sum;
            int L=find_double(s[i].L);
            int R=find_double(s[i].R);
            update(1,1,m,L,R-1,s[i].v);
        }
        printf("Test case #%d\nTotal explored area: %.2lf\n\n",++T,ans);
    }
    return 0;
}