Vijos1755 靶形数独 Sudoku NOIP2009 提高组 T4 舞蹈链 DLX

欢迎访问~原文出处——博客园-zhouzhendong

去博客园看该题解

题目（传送门）

题意概括

给出一个残缺的数独，求这个数独中所有的解法中的最大价值。

一个数独解法的价值之和为每个位置所填的数值乘上该位置的权值，每一个位置的权值如下：

 

 

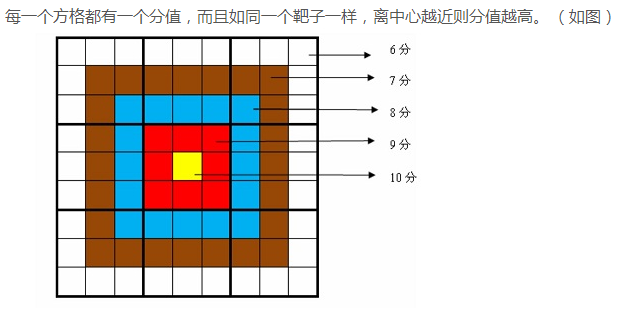
题解

DLX  +  矩阵构建  （两个传送门）

 然后，对于本题，只需要把所有的情况搜光即可。

代码

#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cmath>
using namespace std;
const int N=800,M=400,S=N*4+M;
int a[15][15],xx[N],yy[N],zz[N];
struct DLX{
    int n,m,cnt;
    int x[S],y[S],L[S],R[S],U[S],D[S];
    int C[M],ans,Ans;
    void init(int c){
        memset(x,0,sizeof x),memset(y,0,sizeof y);
        memset(L,0,sizeof L),memset(R,0,sizeof R);
        memset(U,0,sizeof U),memset(D,0,sizeof D);
        memset(C,0,sizeof C);
        m=c;
        for (int i=0;i<=m;i++)
            L[i]=i-1,R[i]=i+1,U[i]=D[i]=i;
        L[0]=m,R[m]=0,cnt=m;
    }
    void link(int i,int j){
        cnt++;
        x[cnt]=i;
        y[cnt]=j;
        L[cnt]=cnt-1;
        R[cnt]=cnt+1;
        D[cnt]=j;
        D[U[j]]=cnt;
        U[cnt]=U[j];
        U[j]=cnt;
        C[j]++;
    }
    void Delete(int k){
        L[R[k]]=L[k];
        R[L[k]]=R[k];
        for (int i=D[k];i!=k;i=D[i])
            for (int j=R[i];j!=i;j=R[j]){
                U[D[j]]=U[j];
                D[U[j]]=D[j];
                C[y[j]]--;
            }
    }
    void Reset(int k){
        L[R[k]]=k;
        R[L[k]]=k;
        for (int i=U[k];i!=k;i=U[i])
            for (int j=L[i];j!=i;j=L[j]){
                U[D[j]]=j;
                D[U[j]]=j;
                C[y[j]]++;
            }
    }
    void solve(){
        if (R[0]==0){
            Ans=max(Ans,ans);
            return;
        }
        int k=R[0];
        for (int i=R[k];i!=0;i=R[i])
            if (C[i]<C[k])
                k=i;
        Delete(k);
        for (int i=D[k];i!=k;i=D[i]){
            ans+=(10-max(abs(xx[x[i]]-5),abs(yy[x[i]]-5)))*zz[x[i]];
            for (int j=R[i];j!=i;j=R[j])
                Delete(y[j]);
            solve();
            for (int j=L[i];j!=i;j=L[j])
                Reset(y[j]);
            ans-=(10-max(abs(xx[x[i]]-5),abs(yy[x[i]]-5)))*zz[x[i]];
        }
        Reset(k);
    }
}dlx;
char s[100];
int hash(int a,int b,int c){
    return a*81+b*9+c+1;
}
int main(){
    for (int i=1;i<=9;i++)
        for (int j=1;j<=9;j++)
            scanf("%d",&a[i][j]);
    dlx.init(324);
    int Row=0;
    for (int i=1;i<=9;i++)
        for (int j=1;j<=9;j++){
            int st,en;
            if (a[i][j]==0)
                st=1,en=9;
            else
                st=en=a[i][j];
            for (int k=st;k<=en;k++){
                Row++;
                xx[Row]=i,yy[Row]=j,zz[Row]=k;
                int first=dlx.cnt+1;
                dlx.link(Row,hash(0,i-1,j-1));
                dlx.link(Row,hash(1,i-1,k-1));
                dlx.link(Row,hash(2,j-1,k-1));
                dlx.link(Row,hash(3,((i-1)/3)*3+(j-1)/3,k-1));
                dlx.L[first]=dlx.cnt;
                dlx.R[dlx.cnt]=first;
            }
        }
    dlx.ans=0,dlx.Ans=-1;
    dlx.solve();
    printf("%d",dlx.Ans);
    return 0;
}