一个简单的旋转控制器与固定屏幕位置

　　如下是初步效果图,后面会用在前面的Ogre编辑器中.

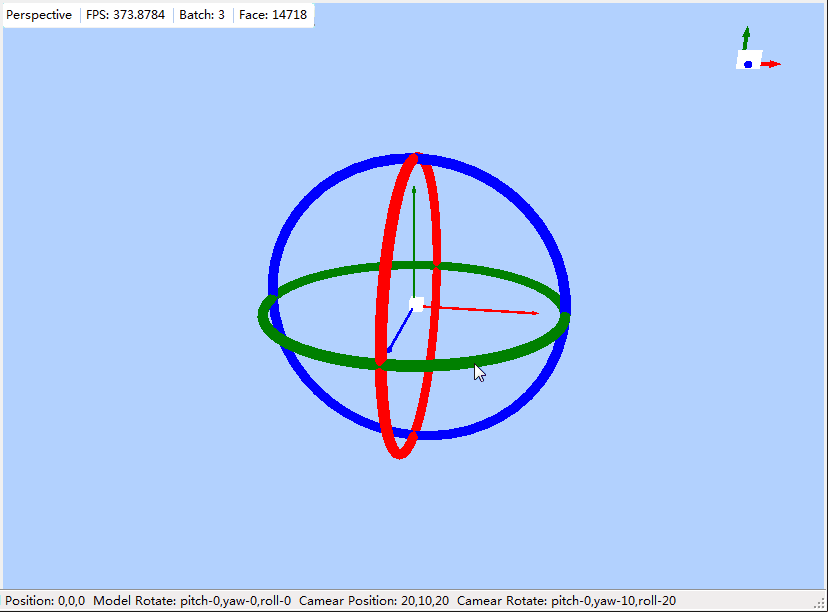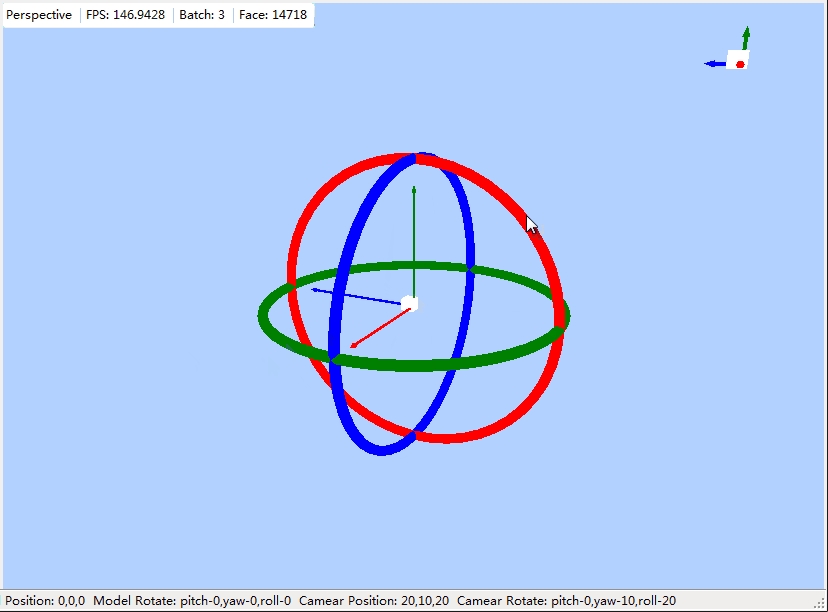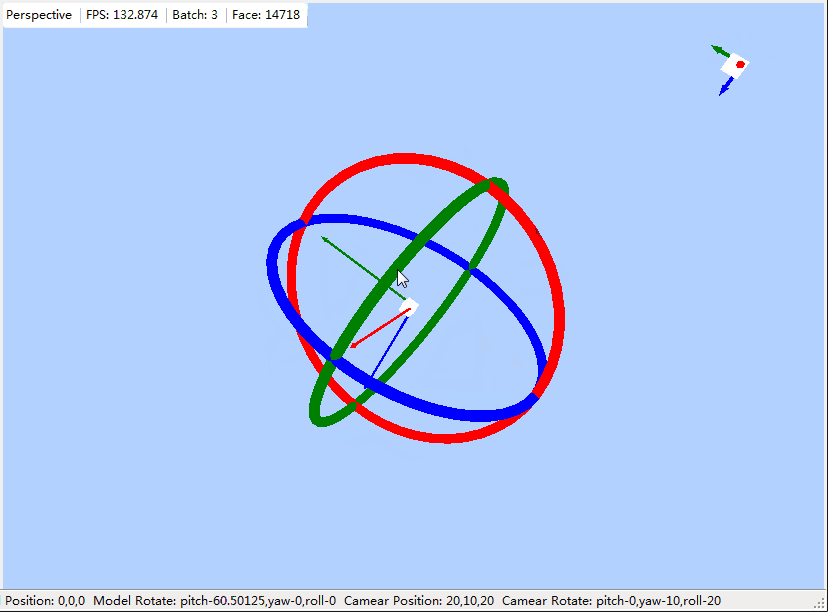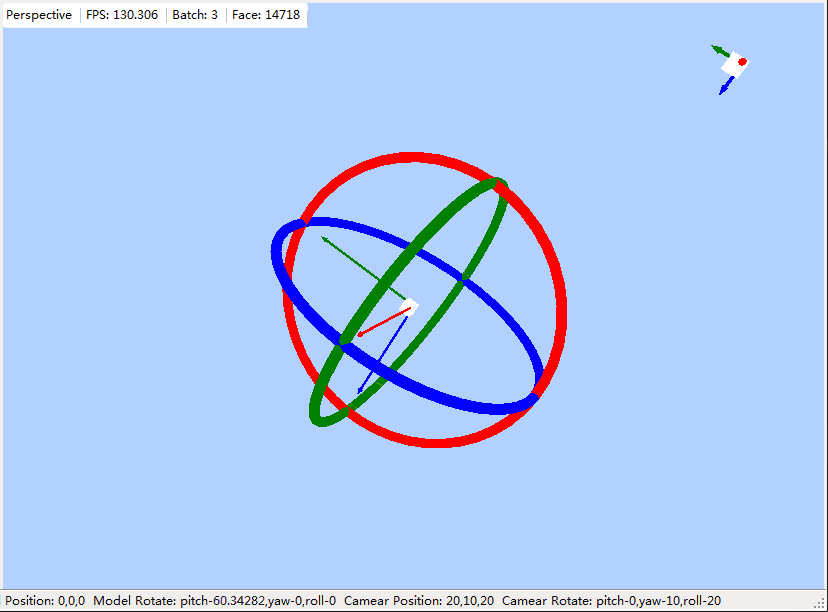
　　开始旋转控制写的比较简单,直接根据鼠标x,y调用yaw与pitch,虽然可用,但是不好用,有时要调到自己想要的方向搞一会,一点都不专业,记的以前好像看过那个软件使用的就是如上这种,分别给出三个方向的圆环,根据鼠标最开始点击的圆环,分别单独调用pitch,yaw,roll,今天花了些时间模仿了下这个,本文记录下.

　　用的是Axiom,Ogre的C#版,代码差不多可以直接换成MOgre的.

　　先生成模型,调用了本项目的一些代码,给出相关位置关键代码.箭头模型.

        public void AddArrow(Vector3 Vector21, Vector3 Vector22, double diameter, double headLength = 3, int thetaDiv = 18)
        {
            var dir = Vector22 - Vector21;
            double length = dir.Length;
            double r = diameter / 2;

            var pc = new List<Vector2>
                {
                    new Vector2(0, 0),
                    new Vector2(0, r),
                    new Vector2(length - (diameter * headLength), r),
                    new Vector2(length - (diameter * headLength), r * 2),
                    new Vector2(length, 0)
                };

            this.AddRevolvedGeometry(pc, null, Vector21, dir, thetaDiv);
        }

        public void AddRevolvedGeometry(IList<Vector2> Vector2s, IList<double> textureValues, Vector3 origin, Vector3 direction, int thetaDiv)
        {
            direction.Normalize();

            // Find two unit vectors orthogonal to the specified direction
            var u = direction.FindAnyPerpendicular();
            var v = direction.Cross(u);

            u.Normalize();
            v.Normalize();

            var circle = GetCircle(thetaDiv);

            int index0 = this.positions.Count;
            int n = Vector2s.Count;

            int totalNodes = (Vector2s.Count - 1) * 2 * thetaDiv;
            int rowNodes = (Vector2s.Count - 1) * 2;

            for (int i = 0; i < thetaDiv; i++)
            {
                var w = (v * circle[i].x) + (u * circle[i].y);

                for (int j = 0; j + 1 < n; j++)
                {
                    // Add segment
                    var q1 = origin + (direction * Vector2s[j].x) + (w * Vector2s[j].y);
                    var q2 = origin + (direction * Vector2s[j + 1].x) + (w * Vector2s[j + 1].y);

                    // TODO: should not add segment if q1==q2 (corner Vector2)
                    // const double eps = 1e-6;
                    // if (Vector3.Subtract(q1, q2).LengthSquared < eps)
                    // continue;
                    this.positions.Add(q1);
                    this.positions.Add(q2);

                    if (this.normals != null)
                    {
                        double tx = Vector2s[j + 1].x - Vector2s[j].x;
                        double ty = Vector2s[j + 1].y - Vector2s[j].y;
                        var normal = (-direction * ty) + (w * tx);
                        normal.Normalize();

                        this.normals.Add(normal);
                        this.normals.Add(normal);
                    }

                    if (this.textureCoordinates != null)
                    {
                        this.textureCoordinates.Add(new Vector2((double)i / (thetaDiv - 1), textureValues == null ? (double)j / (n - 1) : textureValues[j]));
                        this.textureCoordinates.Add(new Vector2((double)i / (thetaDiv - 1), textureValues == null ? (double)(j + 1) / (n - 1) : textureValues[j + 1]));
                    }

                    int i0 = index0 + (i * rowNodes) + (j * 2);
                    int i1 = i0 + 1;
                    int i2 = index0 + ((((i + 1) * rowNodes) + (j * 2)) % totalNodes);
                    int i3 = i2 + 1;

                    this.triangleIndices.Add(i1);
                    this.triangleIndices.Add(i0);
                    this.triangleIndices.Add(i2);

                    this.triangleIndices.Add(i1);
                    this.triangleIndices.Add(i2);
                    this.triangleIndices.Add(i3);
                }
            }
        }

　　这里的代码主要是用到开源项目HelixToolkit里的,我稍微有些改动些以用于Axiom中,大意是先得到圆面控制点,然后按顺序连接圆环面,如上面箭头有五个圆面控制点,第一个和第二个点之间画一个箭头底部面,第二个和第三个点画圆柱体,第三个和第四个点画一个内圈,就是连接圆柱面最上面与箭头底面那个圆圈,第四个与第五个画最前面的箭头部分.通过他的这种,可以画出很多复杂的模型.

　　然后是画外面的三个圆环.如下代码.

public class Torus
    {
        float innerRadius = 0.2f;
        float outerRadius = 5.0f;

        /// <summary>
        /// Initializes a new instance of the <see cref="Torus"/> class.
        /// </summary>
        public Torus(float diameter, float innerDiameter)
        {
            innerRadius = innerDiameter;
            outerRadius = diameter;
            InitialiseTorus();
        }

        /// <summary>
        /// Initialises the torus.
        /// </summary>
        /// <returns></returns>
        private bool InitialiseTorus()
        {
            //  Calculate the number of vertices and indices.
            numVertices = (torusPrecision + 1) * (torusPrecision + 1);
            numIndices = 2 * torusPrecision * torusPrecision * 3;

            //  Create the vertices and indices.
            vertices = new Vector3[numVertices];
            indices = new uint[numIndices];

            //  Calculate the first ring - inner radius 4, outer radius 1.5
            for (int i = 0; i < torusPrecision + 1; i++)
            {
                vertices[i] = new Vector3(innerRadius, 0.0f, 0.0f).GetRotatedZ(i * 360.0f / torusPrecision)
                    + new Vector3(outerRadius, 0.0f, 0.0f);
                //vertices[i].s = 0.0f;
                //vertices[i].t = (float)i / torusPrecision;

                //vertices[i].sTangent.Set(0.0f, 0.0f, -1.0f);
                //vertices[i].tTangent = (new Vertex(0.0f, -1.0f, 0.0f)).GetRotatedZ(i * 360.0f / torusPrecision);
                //vertices[i].normal = vertices[i].tTangent.VectorProduct(vertices[i].sTangent);
            }

            //  Rotate the first ring to get the other rings
            for (uint ring = 1; ring < torusPrecision + 1; ring++)
            {
                for (uint i = 0; i < torusPrecision + 1; i++)
                {
                    vertices[ring * (torusPrecision + 1) + i] =
                        vertices[i].GetRotatedY(ring * 360.0f / torusPrecision);

                    //vertices[ring * (torusPrecision + 1) + i].s = 2.0f * ring / torusPrecision;
                    //vertices[ring * (torusPrecision + 1) + i].t = vertices[i].t;

                    //vertices[ring * (torusPrecision + 1) + i].sTangent =
                    //    vertices[i].sTangent.GetRotatedY(ring * 360.0f / torusPrecision);
                    //vertices[ring * (torusPrecision + 1) + i].tTangent =
                    //    vertices[i].tTangent.GetRotatedY(ring * 360.0f / torusPrecision);
                    //vertices[ring * (torusPrecision + 1) + i].normal =
                    //    vertices[i].normal.GetRotatedY(ring * 360.0f / torusPrecision);
                }
            }
            //  Calculate the indices
            for (uint ring = 0; ring < torusPrecision; ring++)
            {
                for (uint i = 0; i < torusPrecision; i++)
                {
                    indices[((ring * torusPrecision + i) * 2) * 3 + 0] = ring * (torusPrecision + 1) + i;
                    indices[((ring * torusPrecision + i) * 2) * 3 + 1] = (ring + 1) * (torusPrecision + 1) + i;
                    indices[((ring * torusPrecision + i) * 2) * 3 + 2] = ring * (torusPrecision + 1) + i + 1;
                    indices[((ring * torusPrecision + i) * 2 + 1) * 3 + 0] = ring * (torusPrecision + 1) + i + 1;
                    indices[((ring * torusPrecision + i) * 2 + 1) * 3 + 1] = (ring + 1) * (torusPrecision + 1) + i;
                    indices[((ring * torusPrecision + i) * 2 + 1) * 3 + 2] = (ring + 1) * (torusPrecision + 1) + i + 1;
                }
            }

            //  OK, that's the torus done!
            return true;
        }

        /// <summary>
        /// The number of vertices.
        /// </summary>
        private uint numVertices = 0;

        /// <summary>
        /// The number of indices.
        /// </summary>
        private uint numIndices = 0;

        /// <summary>
        /// The torus indices.
        /// </summary>
        private uint[] indices;

        /// <summary>
        /// The torus vertices.
        /// </summary>
        private Vector3[] vertices;

        /// <summary>
        /// We define our torus to have a precision of 48. 
        /// This means that there are 48 vertices per ring when we construct it.
        /// </summary>
        private const uint torusPrecision = 48;

        /// <summary>
        /// Gets the num vertices.
        /// </summary>
        public uint NumVertices
        {
            get { return numVertices; }
        }

        /// <summary>
        /// Gets the num indices.
        /// </summary>
        public uint NumIndices
        {
            get { return numIndices; }
        }

        /// <summary>
        /// Gets the vertices.
        /// </summary>
        public Vector3[] Vertices
        {
            get { return vertices; }
        }

        /// <summary>
        /// Gets the indices.
        /// </summary>
        public uint[] Indices
        {
            get { return indices; }
        }
    }
public static class VertexExtensions
    {
        public static Vector3 GetRotatedX(this Vector3 me, float angle)
        {
            if (angle == 0.0)
                return new Vector3(me.x, me.y, me.z);

            float sinAngle = (float)Math.Sin(Math.PI * angle / 180);
            float cosAngle = (float)Math.Cos(Math.PI * angle / 180);

            return new Vector3(me.x,
                                me.y * cosAngle - me.z * sinAngle,
                                me.y * sinAngle + me.z * cosAngle);
        }

        public static Vector3 GetRotatedY(this Vector3 me, float angle)
        {
            if (angle == 0.0)
                return new Vector3(me.x, me.y, me.z);

            float sinAngle = (float)Math.Sin(Math.PI * angle / 180);
            float cosAngle = (float)Math.Cos(Math.PI * angle / 180);

            return new Vector3(me.x * cosAngle + me.z * sinAngle,
                        me.y,
                        -me.x * sinAngle + me.z * cosAngle);
        }

        public static Vector3 GetRotatedZ(this Vector3 me, float angle)
        {
            if (angle == 0.0)
                return new Vector3(me.x, me.y, me.z);

            float sinAngle = (float)Math.Sin(Math.PI * angle / 180);
            float cosAngle = (float)Math.Cos(Math.PI * angle / 180);

            return new Vector3(me.x * cosAngle - me.y * sinAngle,
                    me.x * sinAngle + me.y * cosAngle,
                    me.z);
        }

        public static Vector3 GetPackedTo01(this Vector3 me)
        {
            Vector3 temp = new Vector3(me.x, me.y, me.z);
            temp.Normalize();

            temp = (temp * 0.5f) + new Vector3(0.5f, 0.5f, 0.5f);

            return temp;
        }

        public static List<Vector3> GetRotatedX(this IList<Vector3> ms, float angle)
        {
            List<Vector3> result = new List<Vector3>(ms.Count);
            foreach (var m in ms)
            {
                result.Add(m.GetRotatedX(angle));
            }
            return result;
        }

        public static List<Vector3> GetRotatedY(this IList<Vector3> ms, float angle)
        {
            List<Vector3> result = new List<Vector3>(ms.Count);
            foreach (var m in ms)
            {
                result.Add(m.GetRotatedY(angle));
            }
            return result;
        }

        public static List<Vector3> GetRotatedZ(this IList<Vector3> ms, float angle)
        {
            List<Vector3> result = new List<Vector3>(ms.Count);
            foreach (var m in ms)
            {
                result.Add(m.GetRotatedZ(angle));
            }
            return result;
        }
    }

　　这部分代码主要取自SharpGL,改动一些代码然后用于现在的项目,另外也有一些,但是不是用的Triangles的方式画的,那种也就差不多只能用在opengl立即模式下,现在的引擎应该都用不了.

　　如下是重点了,绘制与相关鼠标点击算法.

      public enum EulerRotate
    {
        None,
        Yaw,//y
        Pitch,//x
        Roll,//z
    }
      public class DrawRotate : RenderBasic
    {
        private float diameter;
        private float headLength;
        private int thetaDiv;
        private float length;
        private bool bChange = false;

        public float Diameter
        {
            get
            {
                return diameter;
            }
            set
            {
                if (diameter != value)
                {
                    diameter = value;
                    bChange = true;
                }
            }
        }
        public float HeadLength
        {
            get
            {
                return headLength;
            }
            set
            {
                if (headLength != value)
                {
                    headLength = value;
                    bChange = true;
                }
            }
        }
        public int ThetaDiv
        {
            get
            {
                return thetaDiv;
            }
            set
            {
                if (thetaDiv != value)
                {
                    thetaDiv = value;
                    bChange = true;
                }
            }
        }
        public float Lenght
        {
            get
            {
                return length;
            }
            set
            {
                length = value;
            }
        }

        public EulerRotate rotate = EulerRotate.None;

        public DrawRotate()
            : this(5.0f, 0.1f)
        {
        }

        public DrawRotate(float length, float diameter, float headLength = 3, int thetaDiv = 18)
        {
            this.length = length;
            this.diameter = diameter;
            this.headLength = headLength;
            this.thetaDiv = thetaDiv;
            this.bChange = true;
            this.MaterialName = "Material_Base";
            this.Update();
        }

        public void Update()
        {
            if (bChange && this.isVisible)
            {
                this.Vertexs.Reset();

                var builder = new MeshBuilder(false, false);
                builder.AddArrow(Vector3.Zero, Vector3.UnitX * this.length, this.diameter, this.headLength, this.thetaDiv);
                this.Vertexs.AddBatch(builder.Positions, builder.TriangleIndices, ColorEx.Red);

                builder = new MeshBuilder(false, false);
                builder.AddArrow(Vector3.Zero, Vector3.UnitY * this.length, this.diameter, this.headLength, this.thetaDiv);
                this.Vertexs.AddBatch(builder.Positions, builder.TriangleIndices, ColorEx.Green);

                builder = new MeshBuilder(false, false);
                builder.AddArrow(Vector3.Zero, Vector3.UnitZ * this.length, this.diameter, this.headLength, this.thetaDiv);
                this.Vertexs.AddBatch(builder.Positions, builder.TriangleIndices, ColorEx.Blue);

                MeshGeometry3D cube = MeshHelper.CreateCube(Vector3.UnitScale * 0.125, 0.25f);
                this.Vertexs.AddBatch(cube.Positions, cube.TriangleIndices, ColorEx.White);

                Torus torus = new Torus(length + 1, 0.2f);
                this.Vertexs.AddUBatch(torus.Vertices, torus.Indices, ColorEx.Green);
                this.Vertexs.AddUBatch(torus.Vertices.GetRotatedX(90), torus.Indices, ColorEx.Blue);
                this.Vertexs.AddUBatch(torus.Vertices.GetRotatedZ(90), torus.Indices, ColorEx.Red);
                this.UpdateBuffer();
                bChange = false;
            }
        }

        public void HitTest(Ray ray)
        {
            Sphere sphere = new Sphere(this.ParentNode.DerivedPosition, length + 1);
            var result = ray.IntersectsRay(sphere);
            if (result.Item1)
            {
                var h1 = ray.Origin + result.Item2 * ray.Direction - this.ParentNode.DerivedPosition;
                var h2 = ray.Origin + result.Item3 * ray.Direction - this.ParentNode.DerivedPosition;
                var inverseRotate = this.ParentNode.DerivedOrientation.Inverse();
                h1 = inverseRotate * h1;
                h2 = inverseRotate * h2;
                float x1 = Math.Abs(h1.x);
                float y1 = Math.Abs(h1.y);
                float z1 = Math.Abs(h1.z);
                float x2 = Math.Abs(h2.x);
                float y2 = Math.Abs(h2.y);
                float z2 = Math.Abs(h2.z);
                float min1 = Math.Min(x1, Math.Min(y1, z1));
                float min2 = Math.Min(x2, Math.Min(y2, z2));
                float min = Math.Min(min1, min2);
                if (min == x1 || min == x2)
                    rotate = EulerRotate.Pitch;
                else if (min == y1 || min == y2)
                    rotate = EulerRotate.Yaw;
                else if (min == z1 || min == z2)
                    rotate = EulerRotate.Roll;
            }
        }

        public void Rotate(float value)
        {
            if (rotate == EulerRotate.Pitch)
            {
                this.ParentNode.Pitch(value);
            }
            else if (rotate == EulerRotate.Yaw)
            {
                this.ParentNode.Yaw(value);
            }
            else if (rotate == EulerRotate.Roll)
            {
                this.ParentNode.Roll(-value);
            }
        }
    }

　　RenderBasic是一个简单实现Renderable与MovableObject的类,差不多和SimpleRenderable一样,因为这个项目里的模型有些特殊,所以没有用SimpleRenderable,我简单自己重新写了个,在这不影响,换成SimpleRenderable也差不多.

　　Update就是收集模型数据,交给RenderBasic的UpdateBuffer生成缓冲区数据,简单来说,是一个三float顶点,一int颜色的缓冲区,这里Vertexs.AddBatch会自动更新里面的索引数据,这样做主要是整合成一个Pass渲染,提高效率.

　　主要部分来了,HitTest这个函数就是用于检测你点击在那个圆环上.因为Ogre/Axiom自己给的Intersects算法只给出了最近的那个交点,在这我们需要得到这二个交点,简单修改下.　　

       public static System.Tuple<bool, float, float> IntersectsRay(this Ray ray, Sphere sphere)
        {
            var rayDir = ray.Direction;
            //Adjust ray origin relative to sphere center
            var rayOrig = ray.Origin - sphere.Center;
            var radius = sphere.Radius;
          
            // mmm...sweet quadratics
            // Build coeffs which can be used with std quadratic solver
            // ie t = (-b +/- sqrt(b*b* + 4ac)) / 2a
            var a = rayDir.Dot(rayDir);
            var b = 2 * rayOrig.Dot(rayDir);
            var c = rayOrig.Dot(rayOrig) - (radius * radius);

            // calc determinant
            var d = (b * b) - (4 * a * c);

            if (d < 0)
            {
                // no intersection
                return Tuple.Create(false, 0.0f, 0.0f);
            }
            else
            {
                // BTW, if d=0 there is one intersection, if d > 0 there are 2
                // But we only want the closest one, so that's ok, just use the 
                // '-' version of the solver
                float t1 = (-b - Utility.Sqrt(d)) / (2 * a);
                float t2 = (-b + Utility.Sqrt(d)) / (2 * a);
                return Tuple.Create(true, t1, t2);
            }
        }

　　返回的t1与t2分别是射线与球的交点在射线上的位置,现在我们只知道这二个点在球上,如何确定他在那个圆环上了,我们稍微想一下,还是很容易想到的,点击垂直x轴面的圆环时,他的x值必定在0附近,或者这样说,是x,y,z这三个绝对值中最小的.这样我们拿到最少值就可以知道点击的那个环了.

　　注意二点,ray相交后的点是世界坐标系下的,我们比较x,y,z的大小应该是在模型坐标系下,所以我们把点转化,第一个是位置,第二是方向,方向把父方向的逆求出然后相剩就可以了.还有一个位置就是上面所说,二个交点都要求出,因为我们是不管外面还是里面的.

　　刚看到图,发现有个位置还可以说下,右上角有个固定在屏幕位置的模型,这个当时我还走了点弯路,开始是准备如UI那样,去掉视图与透视矩阵,试验发现后面要根据摄像机来转化顶点位置,这样一来,一是比较麻烦,二是每点都通过CPU计算,降低效率.后面发现没必要,直接更新模型的模型矩阵就行,看如下代码.

this.renderWindow.BeforeViewportUpdate += renderWindow_BeforeViewportUpdate;
        void renderWindow_BeforeViewportUpdate(Axiom.Graphics.RenderTargetViewportEventArgs e)
        {
            var currentView = e.Viewport;
            var camera = e.Viewport.Camera;

            var node = EngineCore.Instance.AxisNode;
            var corners = camera.WorldSpaceCorners;

            var p1 = corners[0] + (corners[4] - corners[0]) * 0.02;
            var p2 = corners[2] + (corners[6] - corners[2]) * 0.02;

            var pos = p1 + (p2 - p1) * 0.1;

            node.Position = pos;
            node.Orientation = elementNode.Orientation;
        }

　　这个BeforeViewportUpdate的插入渲染的位置可以看我前文Ogre 监听类与渲染流程中有详细说明.在这里,直接根据视截体,直接定位在视截体的右上面,camera.WorldSpaceCorners是视截体的八个点(世界坐标下),0-3索引分别对应近视面的右上,左上,左下,右下,4-7索引对应远视面的这四个位置.根据线性式取右上角的位置.因为我这边axisNode是直接在根节点下的,所以直接用position就行,他的方向用模型的方向,这样这个节点就可以显示模型现在的方向.这样不管摄像机如何变换,这个节点始终在位置右上角.

　　如果有用Axiom的同学要注意点,node.Position设置值有一个BUG,主要是因为MovableObject.cs中的如下代码.

        public override AxisAlignedBox GetWorldBoundingBox( bool derive )
        {
            if ( derive )
            {
                this.worldAABB = BoundingBox;
                this.worldAABB.Transform( ParentNodeFullTransform );
            }

            return this.worldAABB;
        }

　　把this.wordAABB = BoundingBox改成this.worldAABB = BoundingBox.Clone() as AxisAlignedBox就可,可能是因为原来AxisAlignedBox在C#中是结构体,后面变成类了,这样每次更新节点位置会调用这个函数,然后更新SceneNode时就会更新MovableObject的AABB,这样就导致AABB又Transform了节点矩阵一次,AABB是错误的了,这样在添加前渲染通道前的摄像机可见检测就可能检测不到了.MOgre应该没有这问题.