算法导论-排序(三) 堆排序
目录
1、堆排序介绍
2、堆排序实例
3、c++ 完整代码
4、参考资料
内容
1、堆排序介绍
1.1 、堆是什么
堆是一颗完全二叉树,(设某一个节点为i,根节点从0开始,则其左孩子节点为2*i+1,右孩子节点为2*i+2),堆任意一个非叶节点满足:
Key[i]>=Key[2*i+1] && Key[i]>=Key[2*i+2] 或者 Key[i]<=Key[2*i+1] && Key[i]<=Key[2*i+2],
就是说对于任意一个父节点,要么大于等于子节点,要么小于等于子节点,对于Key[i]>=Key[2*i+1] && Key[i]>=Key[2*i+2]的堆叫做大顶堆;对于 Key[i]<=Key[2*i+1] && Key[i]<=Key[2*i+2]的叫做小顶堆;由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的,小顶堆的堆顶的关键字是所有关键字中最小的
1.2、什么是堆排序
就是在堆的基础上进行排序,如何排序呢?
[1] 首先,从要排序的数组开始建立一个大顶堆(这里以大顶堆说明,如何建大顶堆,下面详解),这样由大顶堆的性质可知,堆顶的数最大;
[2] 然后,交换堆顶key[0]和堆的最后一个元素Key[n-1],Key[0]<->Key[n-1] ,这样最大的数就放到堆的最后Key[n-1]了;由于交换了元素,0 ~ (n-2)的节点可能不满足大顶堆要求,所以然后对堆的Key[0]--Key[n-2]调整为大顶堆;
[3] 将调整好的大顶堆[0~(N-2)],交换堆顶Key[0]和堆的最后一个元素Key[n-2],Key[0]<->Key[n-2],这样,Key[n-2]、Key[n-1]最大的两个数都已经排好了;重新调整[0~(n-3)]为大顶堆;不断重复此过程直到整个排序过程完成
如何建大顶堆呢?
[1] 首先,从最大的非叶节点(设为Key[i])开始,往下进行调整,如果子孩子节点Key[2*i+1]和Key[2*i+2]较大的值比Key[i]的值大,则,交换该节点Key[i]与子节点中较大的节点。然后 以交换后的子节点作为当前节点,往下进行调整,直到遇到叶节点;
[2] 最大非叶节点Key[i]调整完毕后,对节点Key[i-1]进行往下调整,直到出现叶节点;不断重复此过程,直到对根节点往下调整完毕;
下面是建大顶堆的实例:待排序数组为[5 16 3 20 17 4]
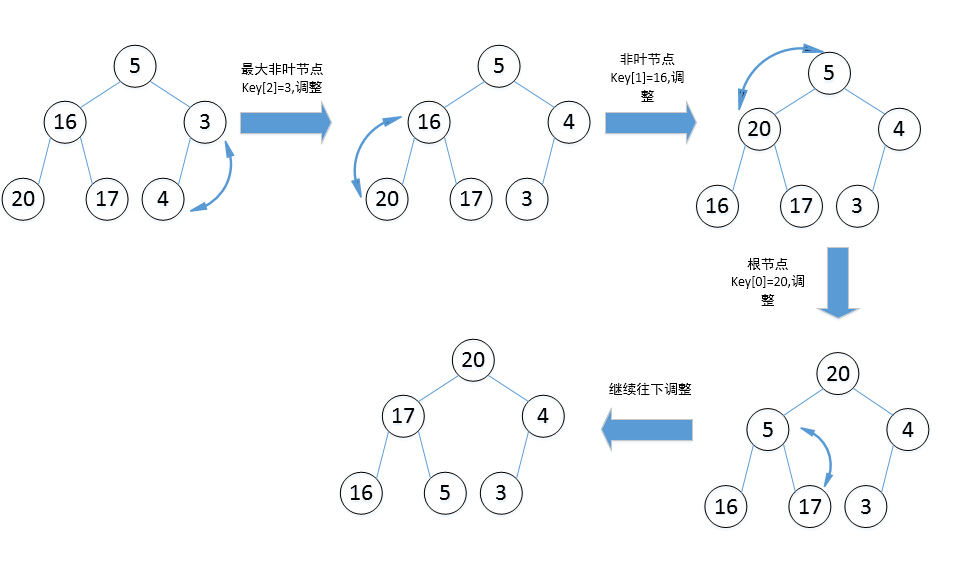
2、堆排序实例
上面图说明了如何建大顶堆,建好大顶堆后就可以进行排序了,下面是堆排序的实例:
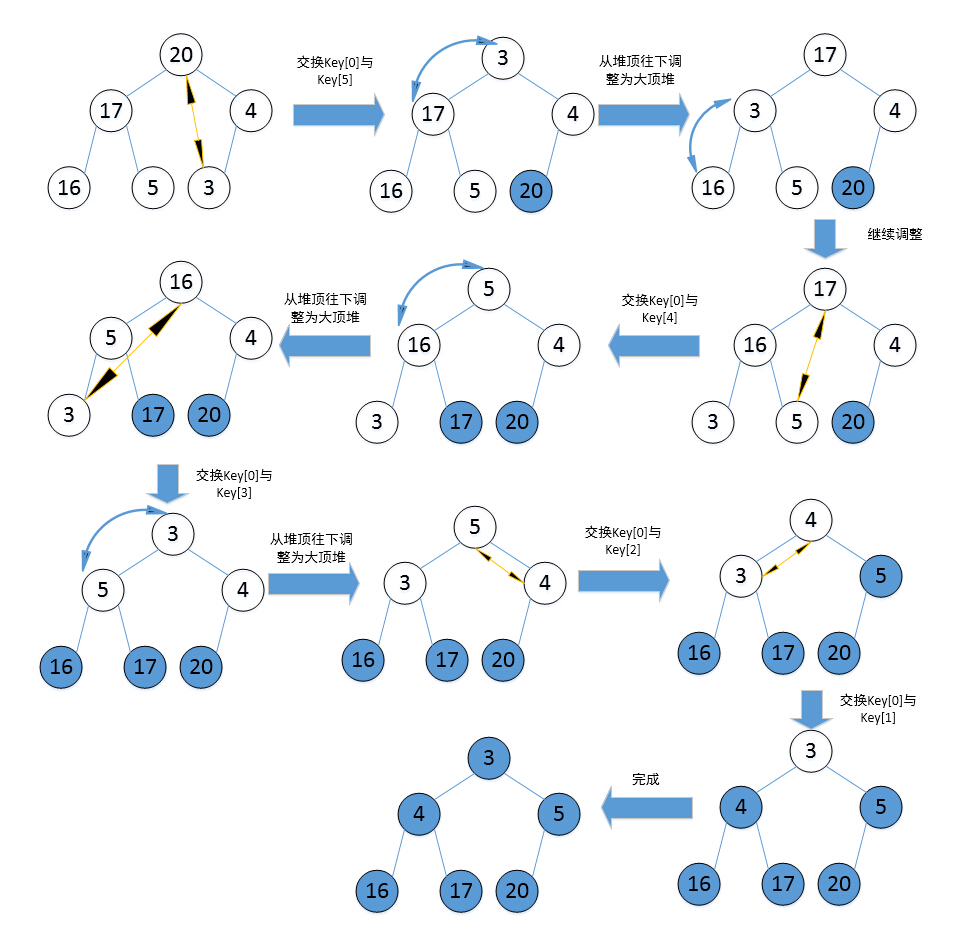
3、c++ 完整代码
Sort.h(堆排序函数实现)
1 #ifndef SORT_HH 2 #define SORT_HH 3 template<typename T > 4 class Sort 5 { 6 public: 7 void Swap(T &m,T &n);//交换数据 8 void print_element(vector<T> A);//打印数组 9 void HeapSort(vector<T> &A,bool IsRecurFlag); 10 private: 11 void HeapAdjust(vector<T> &A,int i,int n);//非递归调整堆 12 void HeapAdjust_Recursive(vector<T> &A,int i,int n);//递归调整堆 13 void BuildBigHeap(vector<T> &A,bool IsRecurFlag);//建大顶堆 14 }; 15 template<typename T>//交换数据 16 void Sort<T>::Swap(T &m,T &n) 17 { 18 T tmp; 19 tmp=m; 20 m=n; 21 n=tmp; 22 } 23 //从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2 24 template<typename T> 25 void Sort<T>::HeapAdjust(vector<T> &A,int i,int n) 26 { 27 T temp = A[i]; 28 int j = 2*i+1;//下标从0开始 29 while (j<n)//非递归实现 30 { 31 if (j+1<n&&A[j+1]>A[j])//找出子节点的最小值 32 j++; 33 if(A[j]<=temp)//子节点不大于父节点,调整结束 34 break; 35 36 A[i] = A[j];// 子节点最大值大于父节点,值赋给父节点; 37 i = j; 38 j = 2*i+1;//下标从0开始 39 } 40 A[i] = temp;//调整结束 41 } 42 //从i节点开始调整,n为节点总数 从0开始计算 i节点的子节点为 2*i+1, 2*i+2 43 template<typename T> 44 void Sort<T>::HeapAdjust_Recursive(vector<T> &A,int i,int n)//递归调整堆 45 { 46 int lchild = 2*i+1; 47 int rchild = 2*i+2; 48 int max = i; 49 if (i<=(n-1)/2)//从最大非叶节点开始调整 50 { 51 if (lchild<n&&A[lchild]>A[max]) 52 { 53 max=lchild; 54 } 55 if(rchild<n&&A[rchild]>A[max]) 56 { 57 max=rchild; 58 } 59 if (max!=i)//子节点值比父节点大,调整 60 { 61 Swap(A[i],A[max]); 62 HeapAdjust_Recursive(A,max,n);//递归 63 } 64 } 65 } 66 //初始从待排序数组建大顶堆 67 //数组从0开始计算,建堆从p到q 68 template<typename T> 69 void Sort<T>::BuildBigHeap(vector<T> &A,bool IsRecurFlag) 70 { 71 int n=A.size(); 72 for(int i=(n-1)/2;i>=0;i--)//从最大的非叶节点开始 73 { 74 if (IsRecurFlag) 75 HeapAdjust_Recursive(A,i,n); 76 else 77 HeapAdjust(A,i,n); 78 } 79 } 80 //堆排序,首先建大顶堆 81 template<typename T> 82 void Sort<T>::HeapSort(vector<T> &A,bool IsRecurFlag) 83 { 84 int len = A.size(); 85 BuildBigHeap(A,IsRecurFlag);//建大顶堆 86 for(int i=len-1;i>=0;i--) 87 { 88 Swap(A[0],A[i]);//未排序堆第一个和最后一个交换 89 if (IsRecurFlag)//递归 90 HeapAdjust_Recursive(A,0,i); 91 else//非递归 92 HeapAdjust(A,0,i);//调整为大顶堆 93 } 94 } 95 96 template<typename T>//打印数组 97 void Sort<T>::print_element(vector<T> A) 98 { 99 int len=A.size(); 100 for (int i=0;i<len;i++) 101 { 102 std::cout<<A[i]<<" "; 103 } 104 std::cout<<std::endl; 105 } 106 #endif
Sort.cpp(主测试函数)
1 #include <iostream> 2 #include <vector> 3 using namespace std; 4 #include "Sort.h" 5 6 int main() 7 { 8 Sort<int> sort1; 9 int a[]={2,4,3,178,23,134,1,-27,1345,80}; 10 vector<int > vec_int1(a,a+10); 11 cout<<"源数组:"; 12 sort1.print_element(vec_int1); 13 cout<<"非递归实现排序:"; 14 sort1.HeapSort(vec_int1,false); 15 sort1.print_element(vec_int1); 16 17 vector<int > vec_int2(a,a+10); 18 cout<<"递归实现排序:"; 19 sort1.HeapSort(vec_int2,true); 20 sort1.print_element(vec_int2); 21 system("PAUSE"); 22 return 0; 23 }
输出:

4、参考资料
【1】 http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html
【2】 http://blog.csdn.net/morewindows/article/details/6709644



 浙公网安备 33010602011771号
浙公网安备 33010602011771号