圆方树总结 [uoj30]Tourists
圆方树总结
所谓圆方树就是把一张图变成一棵树。
怎么变啊qaq
这里盗一张图
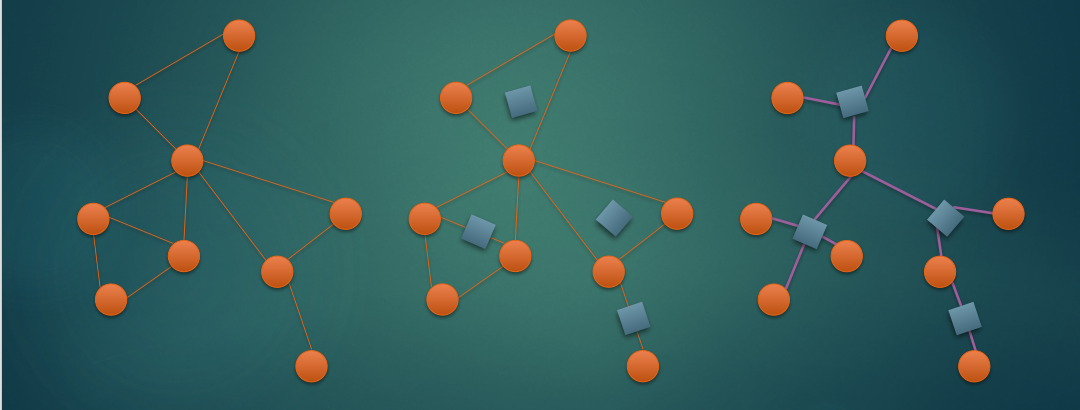
简单来说就是给每一个点双新建一个点,然后连向这个点双中的每一个点。特殊的,把两个点互相连通的也视作一个点双。
我们把原来就有的点称作圆点,因点双而新建的点称之为方点。
这样这棵圆方树就会有一个这样的性质:和每个圆点(方点)相连的点一定是方点(圆点)。
我们在每个圆点上维护这个点原本的信息,在方点上维护这个点双的信息,这样就能完成一些关于一般图的所有简单路径的询问了。
例如:我现在有一张一般图,每个点有一个点权,要求从\(u\)到\(v\)的所有简单路径中经过的最小点权是多少。
可以建出圆方树,在每个方点上维护这个点双中的最小点权,那么每次询问就是查询一个路径最小值了。
如果有修改怎么办呢?直接改完圆点后改和它相邻的方点?
显然这个复杂度是\(O(度数)\)的,很容易卡成\(O(n^2)\)
方法:每个方点维护的信息中不包括它的父亲圆点,这样修改圆点的时候就只需要修改它的父亲方点。查询的时候如果路径的\(lca\)是个方点,就还要再算上它的父亲圆点。
是不是很妙?
uoj30
就是上面讲的那个东西。
圆方树+可删除堆+树链剖分+线段树
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
int gi(){
int x=0,w=1;char ch=getchar();
while ((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if (ch=='-') w=0,ch=getchar();
while (ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return w?x:-x;
}
const int N = 4e5+5;
int n,tot,m,q,val[N],dfn[N],low[N],tim,S[N];
int fa[N],dep[N],sz[N],son[N],top[N],mn[N<<2];
struct Set{
priority_queue<int,vector<int>,greater<int> >Q1,Q2;
void insert(int x){Q1.push(x);}
void erase(int x){Q2.push(x);}
int top(){
while (!Q2.empty()&&Q1.top()==Q2.top()) Q1.pop(),Q2.pop();
return Q1.top();
}
}Q[N];
struct Graph{
int to[N],nxt[N],head[N],cnt;
void link(int u,int v){
to[++cnt]=v;nxt[cnt]=head[u];head[u]=cnt;
to[++cnt]=u;nxt[cnt]=head[v];head[v]=cnt;
}
}G1,G2;
void Tarjan(int u){
dfn[u]=low[u]=++tim;S[++S[0]]=u;
for (int e=G1.head[u];e;e=G1.nxt[e]){
int v=G1.to[e];
if (!dfn[v]){
Tarjan(v),low[u]=min(low[u],low[v]);
if (low[v]>=dfn[u]){
G2.link(++tot,u);int x=0;
do{
x=S[S[0]--];G2.link(tot,x);
}while (x!=v);
}
}
else low[u]=min(low[u],dfn[v]);
}
}
void dfs1(int u,int f){
fa[u]=f;dep[u]=dep[f]+1;sz[u]=1;
if (u<=n&&f) Q[f].insert(val[u]);
for (int e=G2.head[u];e;e=G2.nxt[e]){
int v=G2.to[e];if (v==f) continue;
dfs1(v,u);sz[u]+=sz[v];
if (sz[v]>sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int up){
top[u]=up;dfn[u]=++tim;
if (son[u]) dfs2(son[u],up);
for (int e=G2.head[u];e;e=G2.nxt[e]){
int v=G2.to[e];if (v==fa[u]||v==son[u]) continue;
dfs2(v,v);
}
}
void modify(int x,int l,int r,int p,int v){
if (l==r) {mn[x]=v;return;}
int mid=l+r>>1;
if (p<=mid) modify(x<<1,l,mid,p,v);
else modify(x<<1|1,mid+1,r,p,v);
mn[x]=min(mn[x<<1],mn[x<<1|1]);
}
int query(int x,int l,int r,int ql,int qr){
if (l>=ql&&r<=qr) return mn[x];
int mid=l+r>>1;
if (qr<=mid) return query(x<<1,l,mid,ql,qr);
if (ql>mid) return query(x<<1|1,mid+1,r,ql,qr);
return min(query(x<<1,l,mid,ql,qr),query(x<<1|1,mid+1,r,ql,qr));
}
int main(){
tot=n=gi();m=gi();q=gi();
for (int i=1;i<=n;++i) val[i]=gi();
while (m--){
int u=gi(),v=gi();
G1.link(u,v);
}
for (int i=1;i<=n;++i) if (!dfn[i]) Tarjan(i);
tim=0;dfs1(1,0),dfs2(1,1);
for (int i=1;i<=n;++i) modify(1,1,tot,dfn[i],val[i]);
for (int i=n+1;i<=tot;++i) modify(1,1,tot,dfn[i],Q[i].top());
while (q--){
char ch='%';while (ch!='A'&&ch!='C') ch=getchar();
if (ch=='C'){
int a=gi(),b=gi();
if (fa[a]) Q[fa[a]].erase(val[a]);
val[a]=b;modify(1,1,tot,dfn[a],val[a]);
if (fa[a]) Q[fa[a]].insert(val[a]),modify(1,1,tot,dfn[fa[a]],Q[fa[a]].top());
}
else{
int u=gi(),v=gi(),ans=2e9;
while (top[u]^top[v]){
if (dep[top[u]]<dep[top[v]]) swap(u,v);
ans=min(ans,query(1,1,tot,dfn[top[u]],dfn[u]));
u=fa[top[u]];
}
if (dep[u]>dep[v]) swap(u,v);
ans=min(ans,query(1,1,tot,dfn[u],dfn[v]));
if (u>n) ans=min(ans,val[fa[u]]);
printf("%d\n",ans);
}
}
return 0;
}
圆方树与仙人掌
留坑待补


