BZOJ 1005 [HNOI2008] 明明的烦恼(组合数学 Purfer Sequence)
题目大意
自从明明学了树的结构,就对奇怪的树产生了兴趣......
给出标号为 1 到 N 的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树?
Input
第一行为 N(0<N<=1000),接下来 N 行,第 i+1 行给出第 i 个节点的度数 Di,如果对度数不要求,则输入 -1
Output
一个整数,表示不同的满足要求的树的个数,无解输出 0
做法分析
这题需要了解一种数列: Purfer Sequence
我们知道,一棵树可以用括号序列来表示,但是,一棵顶点标号(1~n)的树,还可以用一个叫做 Purfer Sequence 的数列表示
一个含有 n 个节点的 Purfer Sequence 有 n-2 个数,Purfer Sequence 中的每个数是 1~n 中的一个数
一个定理:一个 Purfer Sequence 和一棵树一一对应
先看看怎么由一个树得到 Purfer Sequence
由一棵树得到它的 Purfer Sequence 总共需要 n-2 步,每一步都在当前的树中寻找具有最小标号的叶子节点(度为 1),将与其相连的点的标号设为 Purfer Sequence 的第 i 个元素,并将此叶子节点从树中删除,直到最后得到一个长度为 n-2 的 Purfer Sequence 和一个只有两个节点的树
看看下面的例子:
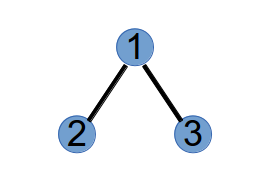
假设有一颗树有 5 个节点,四条边依次为:(1, 2), (1, 3), (2, 4), (2, 5),如下图所示:
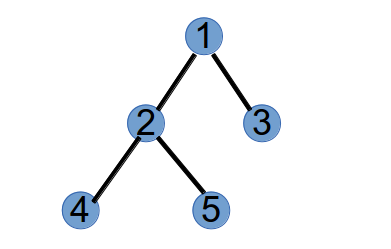
第 1 步,选取具有最小标号的叶子节点 3,将与它相连的点 1 作为第 1 个 Purfer Number,并从树中删掉节点 3:
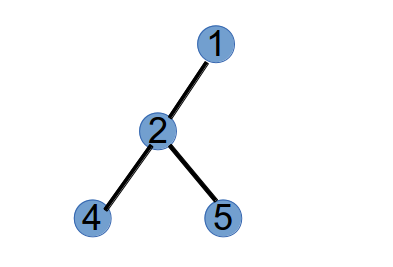
第 2 步,选取最小标号的叶子节点 1,将与其相连的点 2 作为第 2 个 Purfer Number,并从树中删掉点 1:
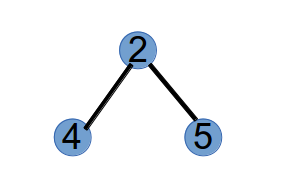
第 3 步,选取最小标号的叶子节点 4,将与其相连的点 2 作为第 3 个 Purfer Number,并从树中删掉点 4:
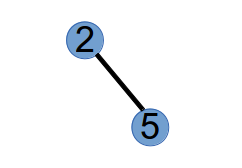
最后,我们得到的 Purfer Sequence 为:1 2 2
不难看出,上面的步骤得到的 Purfer Sequence 具有唯一性,也就是说,一个树,只能得到一个唯一的 Purfer Sequence
接下来看,怎么由一个 Purfer Sequence 得到一个树
由 Purfer Sequence 得到一棵树,先将所有编号为 1 到 n 的点的度赋初值为 1,然后加上它在 Purfer Sequence 中出现的次数,得到每个点的度
先执行 n-2 步,每一步,选取具有最小标号的度为 1 的点 u 与 Purfer Sequence 中的第 i 个数 v 表示的顶点相连,得到树中的一条边,并将 u 和 v 的度减一
最后再把剩下的两个度为 1 的点连边,加入到树中
我们可以根据上面的例子得到的 Purfer Sequence :1 2 2 重新得到一棵树
Purfer Sequence 中共有 3 个数,可以知道,它表示的树中共有 5 个点,按照上面的方法计算他们的度为下表所示:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 2 | 3 | 1 | 1 | 1 |
第 1 次执行,选取最小标号度为 1 的点 3 和 Purfer Sequence 中的第 1 个数 1 连边:

将 1 和 3 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 1 | 3 | 0 | 1 | 1 |
第 2 次执行,选取最小标号度为 1 的点 1 和 Purfer Sequence 中的第 2 个数 2 连边:
将 1 和 2 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 2 | 0 | 1 | 1 |
第 3 次执行,将最小标号度为 1 的点 4 和 Purfer Sequence 第 3 个数 2 连边:

将 2 和 4 的度分别减一:
| 顶点 | 1 | 2 | 3 | 4 | 5 |
| 度 | 0 | 1 | 0 | 0 | 1 |
最后,还剩下两个点 2 和 5 的度为 1,连边:
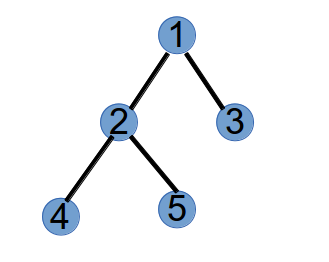
至此,一个 Purfer Sequence 得到的树画出来了,由上面的步骤可知,Purfer Sequence 和一个树唯一对应
综上,一个 Purfer Sequence 和一棵树一一对应
有了 Purfer Sequence 的知识,这题怎么搞定呢?
先不考虑无解的情况,从 Purfer Sequence 构造树的过程中可知,一个点的度数减一表示它在 Purfer Sequence 中出现了几次,那么:
假设度数有限制的点的数量为 cnt,他们的度数分别为:d[i]
另:
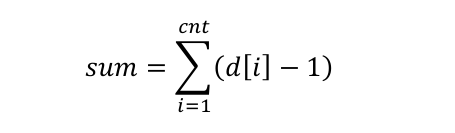
那么,在 Purfer Sequence 中的不同排列的总数为:
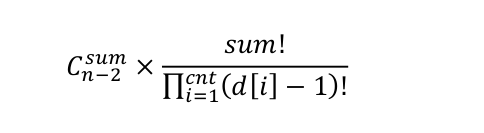
而剩下的 n-2-sum 个位置,可以随意的排列剩余的 n-cnt 个点,于是,总的方案数就应该是:
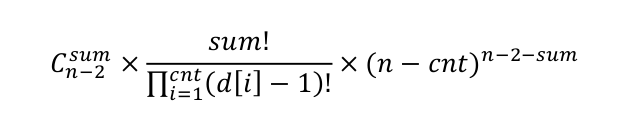
化简之后为:
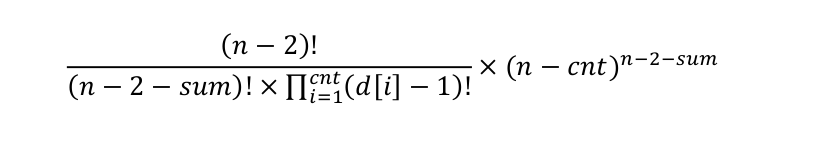
在有解的情况下,计算该结果输出就行了
无解的情况非常好确定,这里就再讨论了
参考代码

1 import java.util.*; 2 import java.math.*; 3 4 public class Main { 5 static int n, d[]=new int[10002]; 6 static BigInteger p[]=new BigInteger[1002]; 7 static BigInteger ans; 8 9 static public void main(String args[]) { 10 Scanner IN=new Scanner(System.in); 11 n=IN.nextInt(); 12 int sum=0, flag=0, cnt=0; 13 for(int i=0; i<n; i++) { 14 d[i]=IN.nextInt(); 15 if(d[i]==0 || d[i]>n-1) flag=1; 16 if(d[i]==-1) continue; 17 sum+=d[i]-1; 18 cnt++; 19 } 20 IN.close(); 21 if(n==1) { 22 if(d[0]==0 || d[0]==-1) System.out.println(1); 23 else System.out.println(0); 24 return; 25 } 26 if(n==2) { 27 if((d[0]==-1 || d[0]==1) && (d[1]==-1 || d[1]==-1)) System.out.println(1); 28 else System.out.println(0); 29 return; 30 } 31 if(flag==1) System.out.println(0); 32 p[0]=BigInteger.ONE; 33 for(int i=1; i<=n; i++) p[i]=p[i-1].multiply(BigInteger.valueOf(i)); 34 ans=p[n-2].divide(p[n-2-sum]); 35 for(int i=0; i<n; i++) { 36 if(d[i]==-1) continue; 37 ans=ans.divide(p[d[i]-1]); 38 } 39 for(int i=0; i<n-2-sum; i++) ans=ans.multiply(BigInteger.valueOf(n-cnt)); 40 System.out.println(ans); 41 } 42 }
题目链接 & AC 通道




